java数据结构和算法10（堆）
这篇我们说说堆这种数据结构，其实到这里就暂时把java的数据结构告一段落，感觉说的也差不多了，各种常见的数据结构都说到了，其实还有一种数据结构是“图”，然而暂时对图没啥兴趣，等有兴趣的再说；还有排序算法，emmm....有时间再看看吧！
其实从写数据结构开始到现在让我最大的感触就是：新手刚开始还是不要看数据结构为好，太无聊太枯燥了，很容易让人放弃；可以等用的各种框架用得差不多了之后，再回头静下心来搞搞数据结构还是挺有趣的；废话不多说，开始今天的内容：
1.二叉树分类
树分为二叉树和多叉树，其实吧有个很有趣的现象，如果树为一叉也就是一个链表（当然没有一叉树这个说法啊，这里是为了好理解）；如果为二叉就是二叉树（包括二叉搜索树，红黑树等）；如果为二叉以上就是为多叉树（包括2-3树，2-3-4树，B树等）
我们再来简单看看二叉树，通过前面的学习我们知道了二叉树是什么鬼，一句话概括就是：除了叶节点外其他的节点最多只有两个子节点；这里我们还可以继续对二叉树进行分类，可以简单的分为完美二叉树，完全二叉树，满二叉树，我们就简单说说这三种分类；
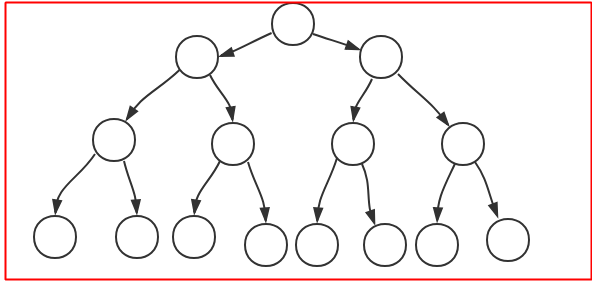
完美二叉树：跟名字差不多，很完美；除了叶节点之外，任意节点都有两个子节点，整棵树可以构成一个大三角形，下图所示：
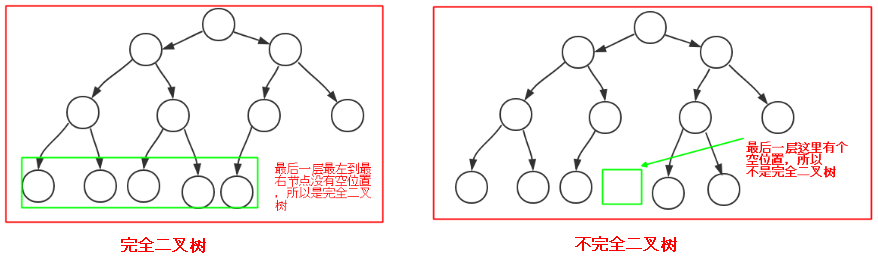
完全二叉树：没有上面的那么完美，只需要从根节点到倒数第二层满足完美二叉树，而最后一层不需要都填满，填满一部分即可，但是最后一层有个要求：从最左边的节点到最右边的节点中间不能有空位置，例如下图：
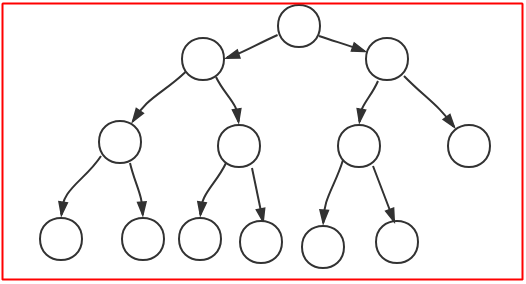
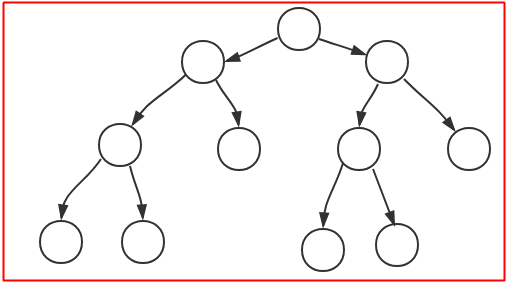
满二叉树：比完全二叉树要求更低，只需要保证除叶节点外，其他节点都有两个子节点，下面两个图都是满二叉树：
2.堆的简介
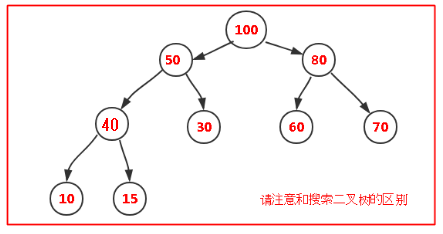
首先我们要明白，此堆非彼堆，我们这里的堆是一种数据结构而不是jvm中的堆内存空间；深入一点来说，堆是一种完全二叉树，通常用数组实现，而且堆中任意一个节点数据都要大于两个子节点的数据，下图所示：
注意，只要子节点两个子节点的数据都比父节点小即可，两个子节点谁大谁小无所谓；
由于堆是由数组实现的，那么数组到底是怎么保存堆中的数据的呢？看下图，其实就是先将第一层数据放入数组，然后将第二层数据从左到右放入数组，然后第三层数据从左到右放入数组....
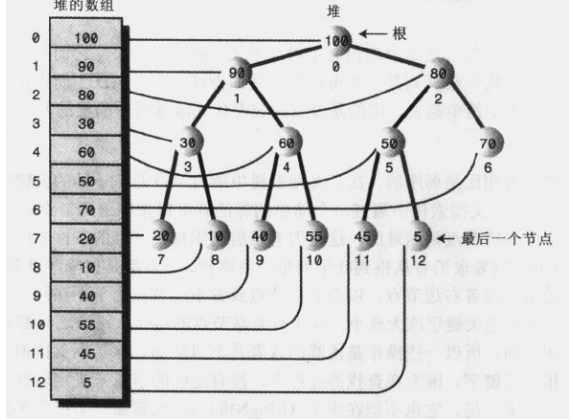
这里补充一个小知识点，后面写java代码实现的时候会用到：在这里我们可以知道堆中的每一个节点都对应于数组中的一个位置，,所以可以根据任意一个节点的位置得出来父节点的位置和两个子节点的位置；举个例子，50这个节点的数组下标是5，那么父节点下标为（5-1）/2向下取整等于2，左子节点下标为2*5+1 = 11；右子节点下标为2*5+2 = 12，我们可以简单归纳一下：
假如一个节点对应的数组下标为a，那么父节点为：（a-1）/2向下取整，左子节点：2a+1，右子节点：2a+2
3.堆的操作
从上面这个图可以看出来堆中的数据放在数组中是没有强制性的顺序的（这里叫做弱序），只能知道数组第一个数最大，最小的数不知道在哪里，而且父节点肯定要比子节点大，除此之外我们就什么也不知道了；
对于数据结构的操作而言无非就是增删改查，我们可以知道在堆中是没有办法进行查询的，因为左右节点没有规定必须哪个大那个小，所以查找的时候不知道应该往哪个子节点去比较，一般而言修改操作是建立在查询的基础上的，所以堆也不支持修改，还有还不支持遍历操作，这样算下来，堆就支持增加和删除操作了，那么下面我们就看看这两个操作；
3.1添加节点
添加节点分为两种情况，第一种，添加的节点数据非常小，直接放在堆的最后一个位置即可（换句话说直接添加到数组有效长度的后面一个空位置即可），这种情况很容易就不多介绍了；第二种，添加节点的数据稍微比较大，比如下面这样的：
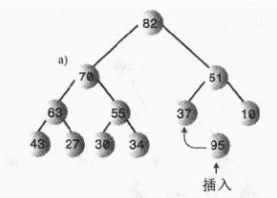
此时堆的结构就被破坏了，我们需要向上调整，那么应该怎么调整呢？很容易，直接和父节点交换位置即可，直到满足堆的这个条件：任意一个父节点都要大于子节点数据
3.2.删除节点
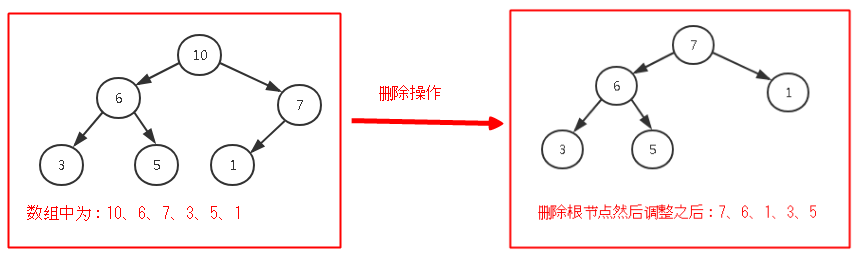
这里的删除指的是删除堆中最大的节点，换句话说就是每次删除都是删除根节点（对应于数组的第一个元素）
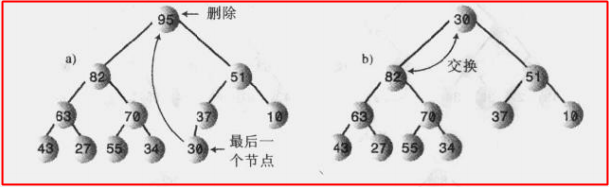
但是删除过后堆的结构就会被破坏，于是要进行调整来平衡堆的结构，看看下图：
我们的做法就是将堆中最后一个节点放在根节点那里（对应于数组就是将数组有效长度的最后元素放在第一个位置那里），然后判断新的根节点是不是比两个子节点中最大的那个还要大？是，不需要调整；否，则将此时新的根节点与比较大的子节点交换位置，然后无限重复这个交换步骤，直到该节点的数据大于两个子节点即可；
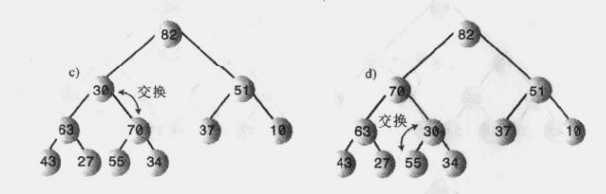
3.3.换位
上面说的换位是什么意思呢？我们知道在java中要交换两个数据要有一个中间变量。如下伪代码：
int a = 3; int b = 10; //交换a和b的数据 int temp； temp = a；//第一步 a = b;//第二步 b = temp;//第三步
可以看到这样的一次简单换位要进行三步复制操作，如果数组中对象很多，都要进行这种换位，那么效率有点低，看看下面这个图；
上图进行三次这样的交换就要经过3x3 = 9次复制操作，那有没有方法可以优化一下呢？
下图所示，用一个临时节点存储A节点，然后D、C、B依次复制到前面的位置，最后就将临时节点放到原来D的位置，总共只需要进行5次复制，这样减少了4次复制，在交换的次数很多的时候这种方式效率可还行。。。
4.java代码
根据上面说的我们用java代码来实现一下堆的添加和删除操作，而且效率都是logN：
package com.wyq.test; public class MyHeap { //堆中的数组要存节点，于是就是一个Node数组 private Node[] heapArray; //数组的最大容量 private int maxSize; //数组中实际节点的数量 private int currentSize; public MyHeap(int size){ this.maxSize = size; this.currentSize = 0; this.heapArray = new Node[maxSize]; } //这里为了方便使用，节点类就为一个静态内部类，其中就存了一个int类型的数据，然后get/set方法 public static class Node{ private int data; public Node(int data){ this.data = data; } public int getData() { return data; } public void setData(int data) { this.data = data; } } //向堆中插入数据，这里有几点需要注意一下；首先，如果数组最大的容量已经存满了，那么插入失败，直接返回false； //然后，数组没有满的话就将新插入的节点放在数组实际存放数据的后一个位置 //最后就是向上调整，将新插入的节点和父节点交换，重复这个操作，直到放在合适的位置，调整完毕，数组实际存放节点数量加一 //下面我们就好好看看向上调整的方法 public boolean insert(int value){ if (maxSize == currentSize) { return false; } Node newNode = new Node(value); heapArray[currentSize] = newNode; changeUp(currentSize); currentSize++; return true; } //向上调增 private void changeUp(int current) { int parent = (current-1)/2;//得到父节点的数组下标 Node temp = heapArray[current];//将我们新插入的节点暂时保存起来，这在前面交换那里说过这种做法的好处 //如果父节点数据小于插入节点的数据 while(current>0 && heapArray[parent].getData()<temp.getData()){ heapArray[current] = heapArray[parent];//这里相当于把父节点复制到当前新插入节点的这个位置 current = parent;//当前指针指向父节点位置 parent = (parent-1)/2;//继续获取父节点的数组下标，然后又会继续比较新插入节点数据和父节点数据，无限重复这个步骤 } //到达这里，说明了该交换的节点已经交换完毕，换句哈来说就是已经把很多个节点向下移动了一个位置，留下了一个空位置，那就把暂时保存的节点放进去就ok了 heapArray[current] = temp; } //删除节点，逻辑比较容易，始终都是删除根节点，然后将最后面一个节点放到根节点位置，然后向下调整就好了；最后就是将实际容量减一就可以了，重点看看向下调整 public Node delete(){ Node root = heapArray[0]; heapArray[0] = heapArray[currentSize-1]; currentSize--; changeDown(0); return root; } //向下调整，大概理一下思路，我们首先将新的根节点临时保存起来，然后要找两个子节点中比较大的那个节点，最后就是比较临时节点和比较大的节点的大小， //如果小，那么把那个比较大的节点往上移动到父节点位置，继续重复这个步骤将比较大的子节点往上移动，最后会留下一个空位置，就把临时节点放进去就好 private void changeDown(int current) { Node largeChild; Node temp = heapArray[0];//临时节点为新的根节点 //注意这个while循环的条件，current<currentSize/2可以保证当前节点至少有一个子节点 while (current<currentSize/2) { int leftIndex = 2*current+1;//左子节点数组下标 int rightIndex = 2*current+2;//右子节点数组下标 int largeIndex;//比较大的子节点数组下标 Node leftChild = heapArray[leftIndex];//左子节点 Node rightChild = heapArray[rightIndex];//右子节点 if (rightIndex<currentSize && leftChild.getData()<rightChild.getData()) { largeChild = rightChild; largeIndex = rightIndex; }else { largeChild = leftChild; largeIndex = leftIndex; } //如果临时节点（即新的根节点）比大的那个子节点还大，那么就直接跳出循环 if (temp.getData() >= largeChild.getData()) { break; } heapArray[current] = largeChild; current = largeIndex;//当前节点的执着呢指向比较大的子节点 } heapArray[current] = temp;//临时节点插入到堆数组中 } //展示堆中的数据 public void display(){ System.out.print("堆中的数据为："); for (int i = 0; i < currentSize; i++) { System.out.print(heapArray[i].getData()+" "); } } public static void main(String[] args) { MyHeap heap = new MyHeap(10); heap.insert(3); heap.insert(5); heap.insert(1); heap.insert(10); heap.insert(6); heap.insert(7); heap.display(); System.out.println(); System.out.print("删除操作之后"); heap.delete(); heap.display(); } }
我们插入的节点如下图所示：
代码测试结果为如下所示，成功；
5.总结
到这里堆就差不多说完了，其实还有个堆排序，其实最简单的就是向堆中添加很多节点，然后不断的删除节点，就会以从大到小的顺序返回了，比较容易吧！当然还可以进行改进不过也很简单，有兴趣的可以自己去看看堆排序。
java数据结构到这里差不多了，就随意列举一下我们用过的数据结构的时间复杂度：
