第二次作业——个人项目实战
【解题思路】
- 找到解题思路,首先要了解数独规则——填入数字1-9,使每个数字在每一行、每一列和每一宫中都只出现一次。
【1】
- 第一思路往往是最简单粗暴的。逐一生成随机数并检验是否符合数度规则,在填完所有宫格后再检验是否为不重复的终盘。
- 完全随机的好处在于完全不用担心不能爆掉N = 1000000的上限,但很容易可以看出暴力破解将会耗费大量的时间和空间资源,只能把它作为垫背的选择。
【2】
- 以暴力破解为突破点,暴力破解的资源损耗在不断的检验数独规则和大量的重复检验工作,我们需要的思路必须去规避或减小这两者的损耗。
- 我的第二思路是依靠暴力的方法先生成一个满足条件的随机数独终盘,然后以当此为种子矩阵,利用矩阵变换来形成新的的终盘。一个已知的终盘通过行、列、行宫、列宫等的交换,最多能再生成54个新的符合规则的终盘。
- 其中,矩阵怎样变换才不会违反数独规则,我参考了这篇博客,该方法一定程度上减轻了生成过程中规则检验的压力,但对查重并无改善。
【3】
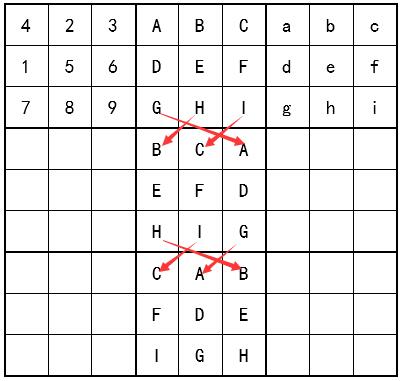
第三思路我希望能直接生成一个符合规则的终盘,省略检验步骤,然后我想到了排列组合。同样需要一个种子,但不像上个方法那样大。生成一个数字1-9的随机数列(种子),放入九大宫格的中央宫,如图
根据数独规则,ABC为456789中A(6, 3)的数字组合排列,DEF为不含123789-ABC中A(X, 3)的数字组合排列,GHI为剩余数字的A(3, 3)排列,abc、def、ghi为同行不曾出现的数字的A(3, 3)排列。
同理,其他宫格……(这一句话曾令我日日夜夜的后悔和懊恼)
现在是9.7凌晨2点,我只想说——本法有误!本法有误!本法有误!这是在我代码实现了大部分的思路之后才发现的,此处应有微笑(强颜欢笑)。以种子宫为核心生成十字宫的终盘后,发现四角宫的数字生成受其横纵向共4个宫中数字的影响,依然需要规则检验。经历前面那样的排列组合,还要再进行检验,我认为这个算法已经失去了其最大的“优势”(我原先以为存在的)。
【4】
在思路三的基础上诞生,依然用随机种子宫生成一行宫(3x9),此时只要保护每个随机种子宫的第一次排列组合A(6, 3)不重复,最大不重复终盘数就能达到8! * A(6, 3) >> 1e6。轻松爆掉N值上限后我就偷了个懒,剩下六个宫的生成方法如下图:
【设计实现】
整体代码框架与调用关系如下:
【核心代码】
void SudoGenerator(int N, int(*sudo)[9])
{
/*变量准备*/
vector<int> seedBox;
vector<int> tmp;
/*初始化种子宫*/
for (int i = 0; i < 9; i++)
seedBox.push_back(i + 1);
while (N != 0)
{
/*获取不重复的种子宫*/
getSeedBox(seedBox);
if (!CheckBoxRepete(seedBox))
{
/*cout << "Box repete!" << endl;*/
continue;
}
/*生成不重复的单排种子*/
tmp.assign(seedBox.begin() + 3, seedBox.end());
Combination_Permutation2(tmp);
int coun = 0;
while (N != 0)
{
if (coun < 120)
InitSudo(sudo, seedBox, coun++);
else
break;
for (int i = 1; i < 3; i++)
{
/*剔除同行已出现的数字*/
tmp.assign(seedBox.begin(), seedBox.end());
tmp.erase(tmp.begin() + 3 * i);
tmp.erase(tmp.begin() + 3 * i);
tmp.erase(tmp.begin() + 3 * i);
/*剔除已被排列的数字*/
for (int j = 0; j < tmp.size(); j++)//i > 0
if (tmp[j] == sudo[0][3] || tmp[j] == sudo[0][4]
|| tmp[j] == sudo[0][5] || tmp[j] == sudo[1][3]
|| tmp[j] == sudo[1][4] || tmp[j] == sudo[1][5])
tmp.erase(tmp.begin() + (j--));
/*保护数独规则*/
if (tmp.size() == 6)
tmp.erase(tmp.begin());
if (tmp.size() == 5)
tmp.erase(tmp.begin());
if (tmp.size() == 4)
tmp.erase(tmp.begin());
/*排列组合*/
tmp = Combination_Permutation1(tmp, tmp.size(), 3);
sudo[i][3] = tmp[0];
sudo[i][4] = tmp[1];
sudo[i][5] = tmp[2];
}
/*第三宫*/
for (int i = 0; i < 3; i++)
{
/*剔除同行出现过的数字*/
tmp.assign(seedBox.begin(), seedBox.end());
for (int j = 0; j < tmp.size(); j++)
if (tmp[j] == sudo[i][0] || tmp[j] == sudo[i][1]
|| tmp[j] == sudo[i][2] || tmp[j] == sudo[i][3]
|| tmp[j] == sudo[i][4] || tmp[j] == sudo[i][5])
tmp.erase(tmp.begin() + (j--));
/*全排列*/
tmp = Combination_Permutation1(tmp, 3, 3);
sudo[i][6] = tmp[0];
sudo[i][7] = tmp[1];
sudo[i][8] = tmp[2];
}
/*余下所有宫格*/
for (int i = 3; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
if (j == 2 || j == 5 || j == 8)
sudo[i][j] = sudo[i - 3][j - 2];
else
sudo[i][j] = sudo[i - 3][j + 1];
}
}
/*输出终盘*/
display(sudo);
N--;
/*cout << "N = " << N << endl;*/
}
}
}
代码思路:
- 代码保护种子宫及生成种子宫后每个终盘惟一一次的A(6, 3)的不重复性,一个种子宫能够被使用120次后失效,失效后产生新的种子宫。以上在代码中实现为两次的while循环。
- 指定九宫格自上而下、从左到右为第一、二、三……八、九宫。
- 生成的种子宫作为数独终盘的第一宫,A(6, 3)生成第二宫的第一行。在扣除A(6, 3)的组合数字之后A(3, 3),得到的排列作为第二宫的第二行,为了保护数独规则不因本次排列组合而破坏,在代码中我简单的排除容器中靠前的数字,来保证第一宫的第三行的数字在本次排列组合之后都被使用掉。最后剩余三个数再次A(3, 3)放入第二宫的第三行。第三宫的每一行都通过排除同行使用过的数字后A(3, 3)来获得当前行的组合数。接下来就是按照上文图片方法生成其余宫。
【测试运行】
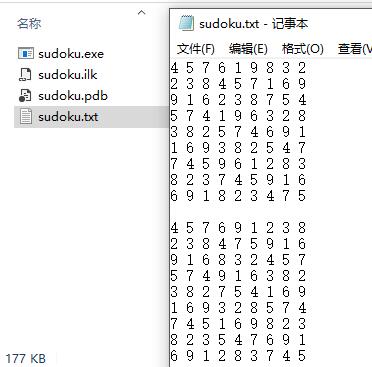
使用命令行执行sudoku.exe应用程序后sudoku.txt将出现在同一目录下。
对于不同编译模式下的运行速度:
| N |Debug x64 | Release x64 |
|-------------------|----------------------|-------------------|
| 10000 | 10s | 1s |
| · 100000 | · 1m30s | 10s |
| 1000000 | 14m | 1m25s |
【性能分析及改进】
【1】
- 实际上,这份代码并非真正的一稿,之前还有另一份完整代码,不过当时比较猴急,直接就改了,没有做过性能分析。采用的是基本相同的思路,不同之处在于,这一份代码在获得种子宫后就直接枚举出所有可能的A(6, 3)情况并存到容器,后续直接访问调用,而上一份代码在A(6, 3)时采用的是即时从种子宫中抽取数字进行组合排列,得到[一个]随机的排列结果,即每次终盘生成都要重新A(6, 3),并需进行重复检验来保证A(6, 3)的结果序列不重复。损耗的时间大致上是现在的30倍,并且会在N = 1000000的时候死机。
【2】
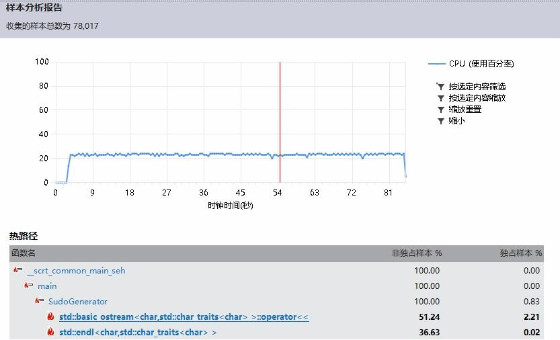
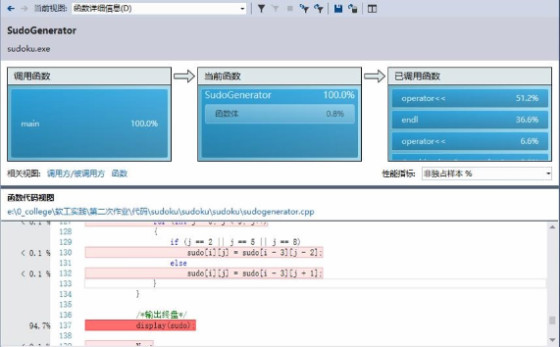
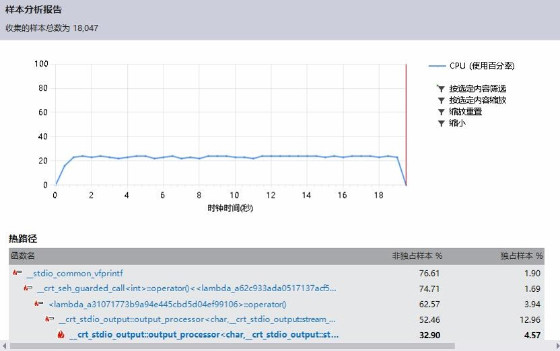
Release x64下性能分析。
可以看到operator << 占了51.2%的时间,其中绝大部分是在display()中被调用的。本代码采用的还是C面向过程的做法,使用cout << 来输出属于个人不够严谨的习惯,需要改进。
这是原先以及修改后display()的代码:
N = 1000000,程序运行时间下降为22s。
再一次,Release x64性能分析。
这一次变成printf()占用时间高,本身已经是使用文件输出了,好像没有办法了。
最终的代码,对于不同编译模式下的运行速度:
| N |Debug x64 | Release x64 |
|-------------------|----------------------|-------------------|
| 10000 | 5s | 小于1s |
| · 100000 | · 56s | 3s |
| 1000000 | 9m08s | 19s |
【过程中遇到的问题与总结】
【1】
- 我自己,包括身边其他讨论的人都遇到的一个问题:随机数的时间种子到底应该放在哪里。看了这篇博文之后豁然开朗,srand()要放在循环外,甚至最好不要放在外部函数中,以避免无意中的反复调用。
【2】
- 在第三思路基本实现是发现思路有误,进行了代码大改,耗费了许多时间精力去修改与取舍,最终的代码就像自己挖了个深坑,找不到东西填上,又舍不得之前费的老大力,最后添添补补,变成不忍直视的一个万里浅坑Orz
- 思路与设计一定要多花时间,反复验证,不能草率。试着计算一下,如果这次在设计和设计复审时多花60m,我在之后的编码阶段应该可以至少节约120m……这次就当吃个教训吧。
【PSP表格】
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 240 | 300 |
| · Estimate | · 估计这个任务需要多少时间 | 240 | 300 |
| Development | 开发 | 3550 | 3050 |
| · Analysis | · 需求分析 (包括学习新技术) | 180 | 80 |
| · Design Spec | · 生成设计文档 | 60 | 240 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 40 | 10 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 20 |
| · Design | · 具体设计 | 240 | 360 |
| · Coding | · 具体编码 | 1200 | 1920 |
| · Code Review | · 代码复审 | 600 | 60 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 1200 | 360 |
| Reporting | 报告 | 260 | 340 |
| · Test Report | · 测试报告 | 120 | 240 |
| · Size Measurement | · 计算工作量 | 20 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 120 | 90 |
| 合计 | 4050 | 3690 |
【关于其他几个问题的思考】
- 问题发源地
问:关于执行力
- 答:关于“基础不扎实”、“拖延”、“荒废时间”等情况,如果将一部分问题的原因归结于“执行力”的问题,这想过去是合情合理的。但我在看到这个问题的时候却突然感性大发,“执行力”肯定是直指问题的直接原因,但是背后是什么导致了执行力的低下,难道是个人性格?说一个人懒是不确切的,毕竟我们依旧爱玩爱闹。在吃饭、睡觉、打王者的时候怎么不懒?怎么执行力就不低下?究其原因,还是背后的动因。如果不能认清自己的所需,强烈的欲望去满足自己所需,自然就执行力低下。比如现在,面临deadline,哪个想交作业的人不是逼着自己在调代码写博文。deadline这时就是动因,推动我们去执行。我倒不是说要有人逼着才走,但如果在自己的心里制定一个aim尚且不够,何不画条deadline?
又想起之前那句话“出来混,总是要还的,你不会的知识,你懒于想通的东西,总是会在一个必要的时候提醒你、惩罚你。”最近老拿这句话吓唬自己。问:关于泛泛而谈
- 答:解决泛泛而谈最直接的方法就是拿出数据。这次的PSP表格就是不错的手段,计划多少时间,实际多少时间,有了记录才能改进。我们平时以“感觉”来作为一件事的测量依据,这就容易让人轻忽,时间一久更是彻底遗忘,不如白纸黑字、事实举证,到头来也算铁证如山,难以泛泛。
- 在此再次重复上次的计划:
“暑假留校进行学习,发现一件事我在2小时以内的专注度和效率是最高,所以我大概每天花费小等于2h的时间来钻研这门课,但下学期课业很重,为了保留时间弹性,每周应该是10~14h。”- 这次的PSP时间记录我做的还不太合理,怎么看我花的时间都应该比记录的长……开学之后我还会做类似于PSP表格的记录。