二叉查找树的实现和删除
树的定义
树是计算机科学中经常用到的一种数据结构。
树是一种非线性的数据结构,以分层的方式 存储数据。
树被用来存储具有层级关系的数据,比如文件系统中的文件;树还被用来存储 有序列表。
选择树而不是那些基本的数据结构,是因 为在二叉树上进行查找非常快(而在链表上查找则不是这样),为二叉树添加或删除元素 也非常快(而对数组执行添加或删除操作则不是这样)。

二叉树
二叉树是一种特殊的树,它的子节点个数不超过两个。二叉树具有一些特殊的计算性质,使得在它们之上的一些操作异常高效
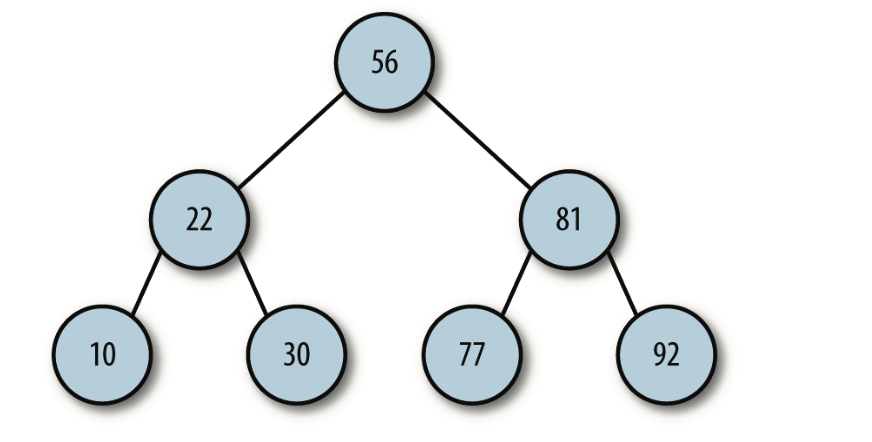
实现二叉树
// node 节点类型
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
this.show = show;
}
// 返回数据
function show() {
return this.data;
}
// 定义BST
function BST () {
this.root = null;
this.insert = insert;
this.inOrder = inOrder;
this.preOrder = preOrder;
this.postOrder = postOrder;
this.getMin = getMin;
this.getMax = getMax;
this.find = find;
this.remove = remove;
this.removeNode = removeNode;
}
二叉树的插入
总体步骤
(1) 设根节点为当前节点。
(2) 如果待插入节点保存的数据小于当前节点,则设新的当前节点为原节点的左节点;反
之,执行第 4 步。
(3) 如果当前节点的左节点为 null,就将新的节点插入这个位置,退出循环;反之,继续
执行下一次循环。
(4) 设新的当前节点为原节点的右节点。
(5) 如果当前节点的右节点为 null,就将新的节点插入这个位置,退出循环;反之,继续
执行下一次循环。
代码实现:
function insert(data) {
var node = new Node(data, null, null);
if (!this.root) {
this.root = node;
} else {
var current = this.root;
var parent;
while(true) {
parent = current;
if (data < current.data) {
current = current.left;
if (!current) {
parent.left = node;
break;
}
} else {
current = current.right;
if (!current) {
parent.right = node;
break;
}
}
}
}
}
二叉树的遍历
- 中序遍历: 按照节点上的键值,升序访问所有节点
- 先序遍历:先访问跟节点,以同样方式访问左子树和右子树
- 后序遍历:先访问叶子节点,从左子树到右子树,到根节点
代码实现:
function inOrder(node) {
if (!(node == null)) {
inOrder(node.left);
putstr(node.show() + " ");
inOrder(node.right);
}
}
function putstr(str) {
console.log(str+"\t")
}
function preOrder(node) {
if (node) {
putstr(node.show() + ' ');
preOrder(node.left);
preOrder(node.right);
}
}
function postOrder(node) {
if (node) {
postOrder(node.left);
postOrder(node.right);
putstr(node.show() + ' ');
}
}
二叉树的删除
二叉树的删除是最复杂的,我们先把实现代码提供
function getMin() {
var current = this.root;
while(!(current.left == null)) {
current = current.left;
}
return current.data;
}
function getMax() {
var current = this.root;
while(!(current.right==null)) {
current = current.right;
}
return current.data;
}
function find(data) {
var current = this.root;
while(current) {
if (data === current.data) {
return current;
} else if (data < current.data) {
current = current.left;
} else {
current = current.right;
}
}
return null
}
function remove(data) {
this.root = removeNode(this.root, data);
}
const getSmallest = function(node) {
if(node.left == null) {
return node;
} else {
return getSmallest(node.left);
}
}
function removeNode(node, data) {
if (node == null) { //当树为空树时
return null;
} else if (node.data == data) { //当当前节点的值为data时
if (node.left == null && node.right == null) { //当当前节点为叶子时
return null;
} else if (node.left == null) { //左子树为空
return node.right;
} else if (node.right == null){ //右子树为空
return node.left;
} else {
var tempNode = getSmallest(node.right);
node.data = tempNode.data;
node.right = removeNode(node.right,tempNode.data);
return node;
}
} else if (data < node.data) {
node.left = removeNode(node.left, data);
return node;
} else {
node.right = removeNode(node.right, data);
return node;
}
}
删除的算法步骤:
- 情况1:删除的当前节点无左右孩子节点,那么就直接将当前要删除的节点设置为null即可。
- 情况2:删除的当前节点无左孩子节点,有右孩子节点,那么就将当前要删除的节点设置为右孩子节点即可。
- 情况3:删除的当前节点无右孩子节点,有左孩子节点,那么就将当前要删除的节点设置为左孩子节点即可。
- 情况4:删除的当前节点有右孩子节点也有左孩子节点,那么就选出右孩子树中最小的点,设置为当前要删除的节点即可。这种方式既可以保证二叉排序树的性质,由于右孩子树中最小的点,无左孩子节点。
public static void main()..
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
// console.log(nums)
nums.inOrder(nums.root);
console.log('------------> ')
// nums.postOrder(nums.root);
// console.log(nums.getMin());
// console.log(nums.getMax());
// console.log(nums.find(16));
nums.remove(22);
console.log(nums);
nums.inOrder(nums.root);



 浙公网安备 33010602011771号
浙公网安备 33010602011771号