高斯金字塔与拉普拉斯金字塔

转载自：https://zhuanlan.zhihu.com/p/32815143

感谢博主。

高斯金字塔：

 

背景知识：
我们都知道，在处理图像的过程中，由于图像中某个像素与相邻像素之间的有很强的相关性，即不管是从纹理还是从灰度级都很相似（CRF的性质，个人理解：一副图像应该就可以看做是一个CRF吧？）

  • 如果物体的尺寸很小或者说对比度不高，通常则需要采用较高的分辨率来观察。
  • 如果物体的尺寸很大或者说对比度很强，那么就仅仅需要较低的分辨率就能够来传观了。
  • 那如果现在物体的尺寸有大有小，对比度有强有弱，这些关系同时存在，这个时候我们该采用何种分辨率呢？

没错，这个时候，只能上多分辨率处理了。

 

图像金字塔：

在讲高斯金字塔之前，我们先来讲讲什么是图像金字塔吧。图像金字塔就是为了以多分辨率来解释图像而诞生的一种简单有效的方法。

 

概念：

  • 一幅图像的金字塔，是以一系列以金字塔形状排列的分辨率初步降低的图像的集合。如下图所示：

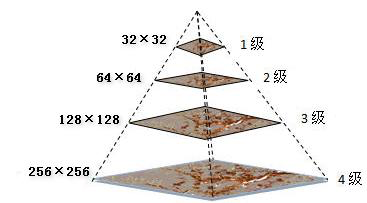
  • 金字塔的底部是待处理图像的高分辨率的表示，而顶部是低分辨率的表示
  • 当金子塔向上层移动的时候，尺寸和分辨率都会降低。
  • 假设基础级（也就是最底层）的尺寸为 2^J \times 2^J 或者用log表示， N \times N (J = log_2^N)
  • 那么金字塔中间任意一级j的尺寸大小为： 2^j \times 2^j, j \in [0,J] ，所以说，一个完整的图像金字塔可以由 J+1 个分辨率集所组成。

OK，有关图像金字塔的概念就讲完了，大家感觉是不是很简单呢？现在就来说说什么高斯金字塔。

其实，在构造上述金字塔的过程中，遵循了如下的流程：

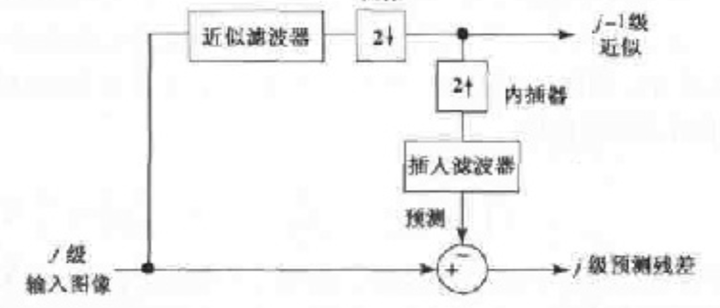
  • 拿到第j级的图像后，先通过一个低通filter，这个filter可以选取我们前面学过的任何一个filter。比如理想低通，巴特沃斯，高斯低通。然后在进行以2为步长的下采样。
  • 这个时候，步骤执行到了一个交汇点处，我们先忽略掉内插器和插入滤波那一部分，那么直接将刚刚第一步得到的结果输出，就得到了j-1级的近似图像。
  • 然后通过第一步+第二步不停的迭代，直到最终输出0级的图像就结束。这个时候，把所有得到的近似图像按照尺寸从大到小进行堆叠，就得到了前面讲的图像金字塔。

 

其实，高斯金字塔的构造过程就是上述的这个过程，只不过在一开始进行滤波的时候，我们只能选择用高斯低通滤波器进行滤波。那有的读者可能会问，什么是高斯低通滤波器呢？当然，我们还是分别从空域和时域来讲：

  • 空域一维形式： \sqrt{2\pi}\delta Ae^{-2\pi^2\delta^2x^2}
  • 频域二维形式： H(u,v) = e^{-\frac{D^2(u,v)}{2\delta^2}}

而频域二维形式往往是我们用的最多的,D(u,v)表示的是(u,v)距离傅里叶变换原点的距离，并且这个原点是经过中心化后的。高斯滤波器在频域的二维形式中有一个非常重要的参数，那就是 \delta ，它表示的是高斯滤波器的带宽，决定了平滑的程度， \delta 越大，那么该filter对应的频带就越宽，平滑程度就越好。

有了上面的介绍后，高斯金字塔就能被我们构建出来了。它其实就是在图像金字塔的构建过程中，增加了两个步骤：

  1. 第一步的滤波必须选用高斯低通filter
  2. 通过使用不同的 \delta 来调节filter的频带宽度，得到经过不同filter相同尺寸的同一组octave

构建结果如下所示：

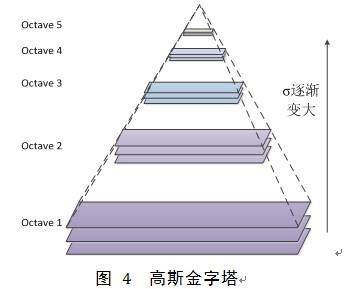
其中的每个octave可以看做是一组图像，这一组图像中的所有图像的分辨率相同，但是采用了不同频带的滤波函数，从模糊的程度上看是有区别的。不同组(octave)之间的图像具有不同的分辨率，在尺度上的差别就更大了。

通过以上步骤建立起来的金字塔就是高斯金字塔了。

最后，来总结下，在图像处理和计算机视觉中，高斯核函数的五个重要性质，这些性质使得它在早期图像处理中特别有用．这些性质表明，高斯平滑滤波器无论在空间域还是在频率域都是十分有效的低通滤波器，：

  1. 二维高斯函数具有旋转对称性，即滤波器在各个方向上的平滑程度是相同的．一般来说，一幅图像的边缘方向是事先不知道的，因此，在滤波前是无法确定一个方向上比另一方向上需要更多的平滑．旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向。
  2. 高斯函数是单值函数。这表明，高斯滤波器用像素邻域的加权均值来代替该点的像素值，而每一邻域像素点权值是随该点与中心点的距离单调增减的。这一性质是很重要的，因为边缘是一种图像局部特征，如果平滑运算对离算子中心很远的像素点仍然有很大作用，则平滑运算会使图像失真。
  3. 高斯函数的傅里叶变换频谱是单瓣的。这一性质是高斯函数傅里叶变换等于高斯函数本身这一事实的直接推论。图像常被不希望的高频信号所污染(噪声和细纹理)。而所希望的图像特征（如边缘），既含有低频分量，又含有高频分量．高斯函数傅里叶变换的单瓣意味着平滑图像不会被不需要的高频信号所污染，同时保留了大部分所需信号。
  4. 高斯滤波器宽度(决定着平滑程度)是由参数σ表征的，而且σ和平滑程度的关系是非常简单的．σ越大，高斯滤波器的频带就越宽，平滑程度就越好。通过调节平滑程度参数σ，可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(欠平滑)之间取得折衷。
  5. 由于高斯函数的可分离性，大高斯滤波器可以得以有效地实现。二维高斯函数卷积可以分两步来进行，首先将图像与一维高斯函数进行卷积，然后将卷积结果与方向垂直的相同一维高斯函数卷积．因此，二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长。

拉普拉斯金字塔：

讲完高斯金字塔，我们再回到这张图：

如果此刻考虑到内插器和插入滤波器的部分，那么此时通过将经过高斯低通滤波器和下采样后的图片经过这两个组件。其实，就是在对这组图像进行近似重建，因为这个过程的所有操作刚刚好和上一个过程（高斯低通滤波器+下采样）是逆过来。

那么通过将重建后的图像和原始的第j级的输入图像进行相减，就得到了j级的预测残差，此时得到的就是拉普拉斯金字塔了。拉普拉斯金字塔的作用是重建高斯金字塔。

posted @ 2018-09-26 08:32  Sunshine168  阅读(13817)  评论(0)  编辑  收藏  举报