L1正则化与L2正则化详解及解决过拟合的方法

欧氏距离（Euclidean distance）也称欧几里得度量、欧几里得度量，是一个通常采用的距离定义，它是在m维空间中两个点之间的真实距离。在二维和三维空间中的欧氏距离的就是两点之间的距离。

Lp space

p范数：║x║p=(|x1|^p+|x2|^p+…+|xn|^p)^{1/p}

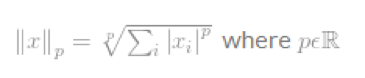
每个值的p次方，加和，求根号p。0就是值加和，1是绝对值的加和，2是平方的加和开2次方。

1范数就是绝对值的和

L0范数是指向量中非0的元素的个数
L1范数是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”（Lasso regularization）。
L2范数: ||W||2。它也不逊于L1范数，它有两个美称，在回归里面，有人把有它的回归叫“岭回归”（Ridge Regression），有人也叫它“权值衰减weight decay”。

重点内容

L1 norm就是绝对值相加，又称曼哈顿距离
L2 norm就是平方和开根号，又称欧几里德距离

在详细介绍L1与L2之前，先讲讲正则化的应用场景。

正则化方法：防止过拟合，提高泛化能力

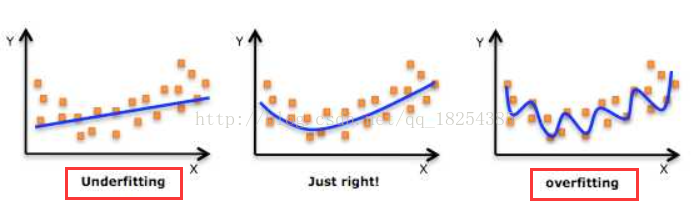
所谓过拟合（over-fitting）其实就是所建的机器学习模型或者是深度学习模型在训练样本中表现得过于优越，导致在验证数据集以及测试数据集中表现不佳。

造成过拟合的本质原因是模型学习的太过精密，导致连训练集中的样本噪声也一丝不差的训练进入了模型。

所谓欠拟合（under-fitting），与过拟合恰好相反，模型学习的太过粗糙，连训练集中的样本数据特征关系（数据分布）都没有学出来。

解决过拟合的方法主要有以下几种：

数据层面：
- 数据集扩增（Data augmentation），获取更多的数据。
- 特征工程，筛选组合得到更高质量的特征。
模型层面：
- 选择较为简单的模型
- 集成学习，Bagging策略组合模型降低模型方差。
- 加入正则项，如L1、L2正则项，以及树模型的剪枝策略，XGBoost中的正则项惩罚（叶子节点值+叶子节点个数）。
更多方法：
- 早停（Early stopping），在模型的训练精度已经到达一定的需求时停止训练，以防止模型学习过多的样本噪声。
- 加入噪声，给定训练样本集更多的样本噪声，使得模型不易完全拟合这些噪声，从而只在大程度上的训练学习我们想要的数据特征关系。
- dropout，在深度学习中，我们经常会使用dropout的方法来防止过拟合，dropout实际上借鉴来bagging的思想。
- 正则化，常用的正则化方法就是加入L1、L2正则项。
- BN（Batch Normalization），BN每一次训练中所组成的Mini-Batch类似于Bagging策略，不同的Mini-Batch训练出来的BN参数也不同。
- 权重衰减（Weight Deacy），有时我们也会称L2正则化为Weight Deacy，因为L2正则化会使得权重偏向于0.Weight Deacy实际上是使得模型在训练后期，权重的变化变得很慢很慢，从而使得模型不至于在迭代后期转而去学习更多的样本噪声。常用的权重衰减方法有滑动平均（Moving Average）

本文着重讲解解决过拟合问题的两大正则方法L1（Lasso）与L2（Ridge）。

在介绍L1、L2之前，我们稍微谈一下L0。在谈L0之前还要稍微讲一下何为范数。

范数(norm）

数学上，范数是一个向量空间或矩阵上所有向量的长度和大小的求和。简单一点，我们可以说范数越大，矩阵或者向量就越大。

L-P范数

$Lp=\sqrt[p]{\sum\limits_{1}^n x_i^p},x=(x_1,x_2,\cdots,x_n)$

例如一个向量：，其欧几里得范数（2-范数）为：

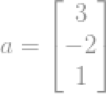
L1-norm

L1范数是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”（Lasso regularization）。现在我们来分析下这个价值一个亿的问题：为什么L1范数会使权值稀疏？有人可能会这样给你回答“它是L0范数的最优凸近似”。实际上，还存在一个更美的回答：任何的规则化算子，如果它在 $W_i=0$ 的地方不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子就可以实现稀疏。这说是这么说，W的L1范数是绝对值，|w|在w=0处是不可微，但这还是不够直观。这里因为我们需要和L2范数进行对比分析。

既然L0可以实现稀疏，为什么不用L0，而要用L1呢？个人理解一是因为L0范数很难优化求解（NP难问题，L0为一个0-1跃阶函数，低于1范数的都不是凸的），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。所以大家才把目光和万千宠爱转于L1范数。

OK，来个一句话总结：L1范数和L0范数可以实现稀疏，L1因具有比L0更好的优化求解特性而被广泛应用。

让我们的参数稀疏有什么好处呢？这里扯两点：

特征选择(Feature Selection)：大家对稀疏规则化趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说，xi的大部分元素（也就是特征）都是和最终的输出yi没有关系或者不提供任何信息的，在最小化目标函数的时候考虑xi这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的信息反而会被考虑，从而干扰了对正确yi的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为0。简单来讲，越好的特征包含的数据分布信息越多，差的特征也包含一定的数据分布信息，但同时还会包含大量的噪声，特征选择旨在于选择出好的特征去学习，而不是为了一点点的模型训练提升去引入学习更多的噪声。
可解释性(Interpretability)：另一个青睐于稀疏的理由是，模型更容易解释。最后的模型输出是关于一堆特征的加权组合，如果特征有几千个，解释起来就很困难。但如果通过特征选择过滤出来5个特征，然后经过训练发现效果也不错，那这样的模型在解释起来就容易多了。

L2-Norm

除了L1范数，还有一种更受宠幸的规则化范数是L2范数: $\left \| W \right \|_2$ 。它也不逊于L1范数，它有两个美称，在回归里面，有人把有它的回归叫“岭回归”（Ridge Regression），有人也叫它“权值衰减weight decay”。这用的很多吧，因为它的强大功效是改善机器学习里面一个非常重要的问题：过拟合。

L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的规则项 $\left \| W \right \|_2$ 最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别的哦。L2的作用就是让所有的参数都接近于0，个人理解，L2的优越性并不主要体现在让参数变小上，关键是在于让所有的参数比较均衡。也就是说所有的特征的表达能力都差不多。这样就不至于让模型对某个特征特别敏感，也就是说在测试集上运行的时候，即使某个特征上有噪声异常突出，但对于整体模型的输出而言，并不会被这个噪声带偏特别多。

L2范数的好处是什么呢？这里也扯上两点：

学习理论的角度：从学习理论的角度来说，L2范数可以防止过拟合，提升模型的泛化能力。
优化计算的角度：从优化或者数值计算的角度来说，L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题。参见L2范数之解救矩阵病态

L1-Norm与L2-Norm

The main difference between L1 and L2 regularization is that L1 can yield sparse models while L2 doesn't. Sparse model is a great property to have when dealing with high-dimensional data, for at least 2 reasons.

Model compression: increasingly important due to the mobile growth

Feature selection: it helps to know which features are important and which features are not or redundant.

What is the difference between L1 and L2 regularization? How does it solve the problem of overfitting? Which regularizer to use and when?

翻译过来就是，L1与L2正则化的主要差别在于L1正则化可以产出稀疏的模型但L2正则化不行。稀疏模型具有更好的特性去处理高维的数据特征，至少有以下两个原因成立：

模型压缩：（不怎么好翻译）随着训练的进行，那些真正有用的特征的重要性逐渐提高。
特征选择：可以帮助我们知道哪些特征是重要的，哪些特征是不重要的。

For simplicity, let's just consider the 1-dimensional case.

L2-regularized loss function $F(x)=f(x)+\lambda\left \| x \right \|_2^2$ is smooth. This means that the optimum is the stationary point (0-derivative point). The stationary point of F can get very small when you increase $\lambda$ , but still won't be 0 unless $f^{'}{(0)=0}$ .

L1-regularized loss function $F(x)=f(x)+\lambda\left \| x \right \|_1$ is non-smooth. It's not differentiable at 0. Optimization theory says that the optimum of a function is either the point with 0-derivative or one of the irregularities (corners, kinks, etc.). So, it's possible that the optimal point of F is 0 even if 0 isn't the stationary point of f. In fact, it would be 0 if $\lambda$ is large enough (stronger regularization effect). Below is a graphical illustration.

In multi-dimensional settings: if a feature is not important, the loss contributed by it is small and hence the (non-differentiable) regularization effect would turn it off.

翻译过来就是：

简单来说，我们只考虑一维情形。L2正则化的损失函数 $F(x)=f(x)+\lambda\left \| x \right \|_2^2$ 是光滑的，这意味着它的最优点是一个固定的点（在损失函数导数为0处），如果我们增大 $\lambda$ ，那么这个点的函数值 $F$ 会变得很小。但它不会是0，除非 $f^{'}{(0)=0}$ 。

L1正则化的损失函数是 $F(x)=f(x)+\lambda\left \| x \right \|_1$ 是不光滑的，在 $x=0处不可导$ 处不可导，最优化理论告诉我们，函数的最优点在导数为0处或者非规则点（不可导的点）处取到。 $x=0处不可导$ 有可能作为函数 $F$ 的最优点，即使 $x=0处不可导$ 不是可导的。事实上，当 $\lambda$ 足够大的时候（强正则影响），最优点确实会在 $x=0处不可导$ 处取到。