druid Approximate Histograms
以下内容翻译自:https://metamarkets.com/2013/histograms/
我要感谢XavierLéauté的广泛贡献(特别是建议几个算法改进和实施工作),有用的评论和富有成效的讨论。特色图片由CERN提供。
许多企业关心的是在关键指标上准确计算分位数,这可能会带来一些大规模的有趣挑战。例如,许多服务级别协议取决于这些指标,例如保证95%的查询在<500ms内返回。互联网服务提供商通常使用可突发计费,这一事实被Google着名利用,可以免费在美国境内传输数TB的数据。分位数计算只涉及对数据进行排序,这可以很容易地并行化。然而,这需要存储原始值,这与预先聚合步骤不一致,这有助于德鲁伊达到如此令人眼花缭乱的速度。相反,我们将这些值的较小的自适应近似值存储为我们的“近似直方图”的构建块。在这篇文章中,我们探索了准确估计分位数和构建直方图可视化的相关问题,这些问题能够实时探索值的分布。我们的解决方案能够在几秒钟内扩展到汇总数十亿的价值。
德鲁伊总结
当我们第一次见到德鲁伊时,我们考虑了以下原始展示事件日志示例:
| timestamp | publisher | advertiser | gender | country | click | price |
|---|---|---|---|---|---|---|
| 2011-01-01T01:01:35Z | bieberfever.com | google.com | Male | USA | 0 | 0.65 |
| 2011-01-01T01:03:63Z | bieberfever.com | google.com | Male | USA | 0 | 0.62 |
| 2011-01-01T01:04:51Z | bieberfever.com | google.com | Male | USA | 1 | 0.45 |
| … | … | … | … | … | … | … |
| 2011-01-01T01:00:00Z | ultratrimfast.com | google.com | Female | UK | 0 | 0.87 |
| 2011-01-01T02:00:00Z | ultratrimfast.com | google.com | Female | UK | 0 | 0.99 |
| 2011-01-01T02:00:00Z | ultratrimfast.com | google.com | Female | UK | 1 | 1.53 |
通过在时间戳列中放弃一些分辨率(例如,通过将时间戳截断为小时),我们可以通过按维度分组并聚合度量来生成汇总数据集。 我们还引入了“展示次数”列,该列根据维度组合计算原始数据中的行数:
| timestamp | publisher | advertiser | gender | country | impressions | clicks | revenue |
|---|---|---|---|---|---|---|---|
| 2011-01-01T01:00:00Z | ultratrimfast.com | google.com | Male | USA | 1800 | 25 | 15.70 |
| 2011-01-01T01:00:00Z | bieberfever.com | google.com | Male | USA | 2912 | 42 | 29.18 |
| 2011-01-01T02:00:00Z | ultratrimfast.com | google.com | Male | UK | 1953 | 17 | 17.31 |
| 2011-01-01T02:00:00Z | bieberfever.com | google.com | Male | UK | 3194 | 170 | 34.01 |
如果我们满足于可以有效分配的计算,例如汇总每小时收入以产生每日收入或计算点击率,那么一切都很好。 在Gray等人的语言中,前者的计算是分布式的:我们可以将原始事件价格相加,以便在每个维度组合上产生小时收入,并进而对该中间人进行求和,以进一步粗化为每日和每季度总计。 后者是代数的:它是固定数量的分布式统计数据的组合,尤其是点击次数/印象数。
但是,当人们想要询问某些投标级数据的问题时,总和和平均值几乎没有用。 交易所可能希望可视化出价格局,以便向出版商提供有关如何设定楼层价格的指导。 由于我们的数据汇总过程,我们已经失去了单独的出价 - 并且知道20个总出价达到5won'ttellowowmanyexceed1或$ 2。 相比之下,分位数是整体的:对于精确描述子集合所需的存储大小没有恒定的约束。
虽然原始数据包含纯粹的价格 - 我们可以准确地回答这些出价格局问题 - 让我们回想一下为什么我们更喜欢汇总数据集。 在上面的示例中,每个原始行对应一次展示,而汇总数据表示平均压缩比为~2500:1(实际上,我们看到1到3位数范围内的比率)。 较少的数据既可以更便宜地存储在内存中,也可以更快地扫描。 实际上,我们正在通过这种预聚合来减少增加的ETL工作量,以减少存储和更快的查询。
支持分位数查询的一种解决方案是在每行中存储~2500个价格的整个数组:
| timestamp | publisher | advertiser | gender | country | impressions | clicks | prices |
|---|---|---|---|---|---|---|---|
| 2011-01-01T01:00:00Z | ultratrimfast.com | google.com | Male | USA | 1800 | 25 | [0.64, 1.93, 0.93, …] |
| 2011-01-01T01:00:00Z | bieberfever.com | google.com | Male | USA | 2912 | 42 | [0.65, 0.62, 0.45, …] |
| 2011-01-01T02:00:00Z | ultratrimfast.com | google.com | Male | UK | 1953 | 17 | [0.07, 0.34, 1.23, …] |
| 2011-01-01T02:00:00Z | bieberfever.com | google.com | Male | UK | 3194 | 170 | [0.53, 0.92, 0.12, …] |
但是这种方法的存储要求令人望而却步。 如果我们可以接受近似分位数,那么我们可以用存储中的次线性数据结构替换完整的价格数组 - 类似于我们基于草图的基数估算方法。
近似直方图
Ben-Haim和Tom-Tov建议总结具有固定数量(计数,质心)对的无界长度数组。假设我们尝试用一对数汇总一组数字。均值(质心)具有最小化它与每个值之间的平方差之和的良好特性,但由于平方,它对异常值敏感。中位数是绝对差值之和的最小值,对于奇数个观测值,对应于实际投标价格。由于第二次价格拍卖的机制,投标价格往往会出现偏差 - 一些投标人出价100没有问题,因为他们知道他们只会非常喜欢2。因此,“平均”bidpricethanameanof20的中位数为1ismoresentative。然而,使用(计数,中位数)表示法,没有办法合并中位数:知道8个价格的中位数为.43和10个星期五,而不是告诉你所有18个价格的中位数是0.44美元。合并质心很简单 - 只需使用加权平均值即可。给定(计数,质心)对的一些近似直方图表示,我们可以在扫描数据时进行在线更新。
当然,没有办法用一对精确地总结任意数量的价格,因此我们面临经典的准确度/存储/速度权衡。我们可以像这样修复我们存储的对的数量:
| timestamp | publisher | advertiser | gender | country | impressions | clicks | AH_prices |
|---|---|---|---|---|---|---|---|
| 2011-01-01T01:00:00Z | ultratrimfast.com | google.com | Male | USA | 1800 | 25 | [(1, .16), (48, .62), (83, .71), …] |
| 2011-01-01T01:00:00Z | bieberfever.com | google.com | Male | USA | 2912 | 42 | [(1, .12), (3, .15), (30, 1.41), …] |
| 2011-01-01T02:00:00Z | ultratrimfast.com | google.com | Male | UK | 1953 | 17 | [(2, .03), (1, .62), (20, .93), …] |
| 2011-01-01T02:00:00Z | bieberfever.com | google.com | Male | UK | 3194 | 170 | [(1, .05), (94, .84), (1, 1.14), …] |
在第一行中,有一个出价为.16,48bidswithanaveragepriceof.62,依此类推。 但是考虑到一组价格,我们如何将它们总结为(计数,质心)对? 这是k均值聚类问题的一个特例,即使在平面上,它通常也是NP难的。 然而,幸运的是,一维案例易于处理,并通过动态编程获得解决方案。 B-H / T-T方法是通过采用加权平均来迭代地将最接近的两对组合在一起,直到达到我们期望的大小。
这里我们说明了对于整数1到10,15和20以及12和25的B-H / T-T汇总过程,每个重复3次,对于(计数,质心)对的3个不同选择。
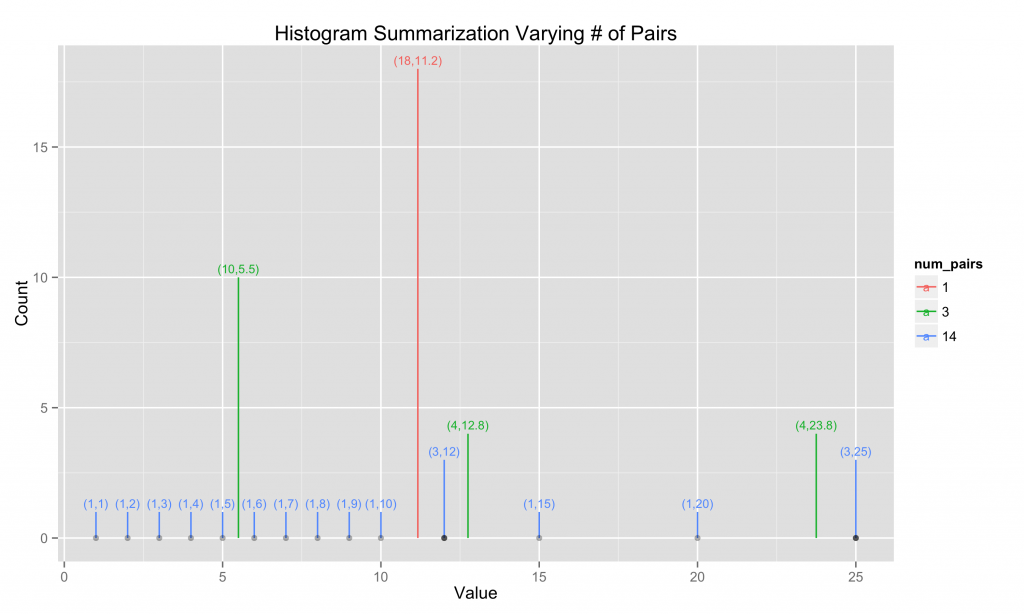
这些近似直方图对象有4个显着操作:
向直方图添加新值:添加新对,(1,值),如果超出size参数,则合并最近的对
将两个直方图合并在一起:重复将所有值对从一个直方图添加到另一个直方图
估计低于某个参考值的值的计数:在对之间构建梯形并查看各个区域
估计直方图中表示的值的分位数:沿着梯形走,直到达到所需的分位数
我们在ETL阶段应用操作1,因为我们按维度分组并在结果价格上构建直方图,将此对象序列化为德鲁伊数据段。计算节点并行地重复操作2,每个计算节点向查询代理发出中间直方图以进行组合(操作2的另一个应用)。最后,我们可以重复应用操作3来估计各个断点之间的计数,从而产生直方图。或者我们可以通过操作4估计感兴趣的分位数。
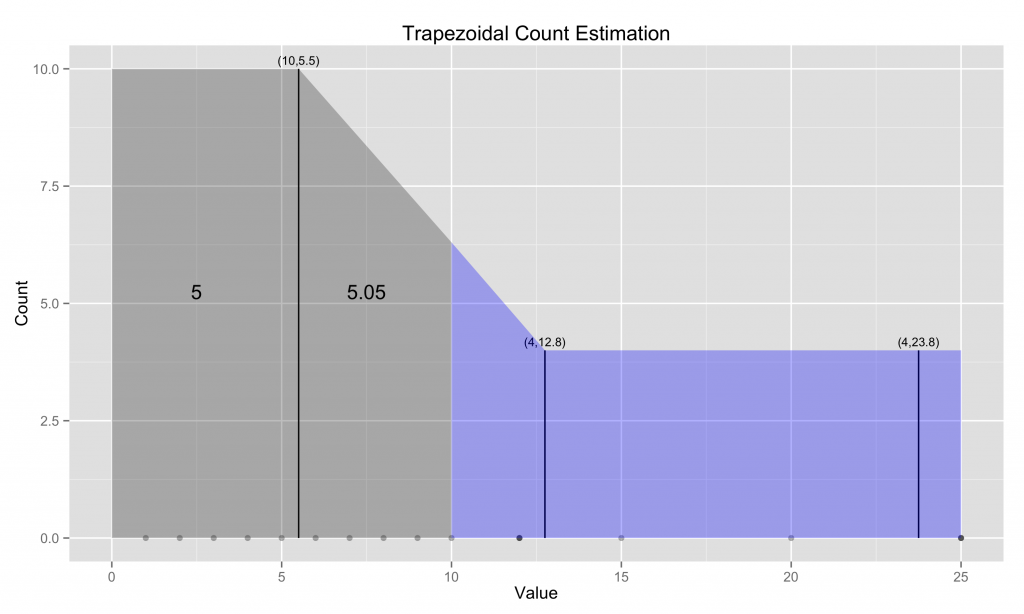
在这里,我们以一个例子来回顾Ben-Haim和Tom-Tov的梯形估计。假设我们想要估计小于或等于10的值的数量(确切答案是10),知道平均值为5.5的4个点,平均值为12.8的4个点,以及平均值为23.8的4个点。我们假设一半的值位于左侧,另一半位于质心的右侧(我们将在下一节中对此假设进行改进)。所以我们标记出5个值小于第一个质心(这证明是正确的)。然后我们绘制一个连接下两个质心的梯形,并假设5.5和10之间的值的数量与该子梯形占据的面积成比例(后半部分用蓝色标记)。我们假设靠近5.5的10个值中的一半位于其右侧,并且靠近12.8的4个值中的一半位于其左侧,并且将7的总和乘以区域的比率,得出该区域中我们估计的5.05(确切的答案是5)。因此,我们估计有10.05个值小于或等于10。
改进
在这里,我们描述了我们实施B-H / T-T近似直方图的一些改进和效率。
查询时的计算效率(操作2)对我们来说比ETL时间(操作1)更加珍贵。也就是说,如果它允许非常有效的组合方式,我们可以花费更多的周期来构建直方图。我们使用堆来跟踪对之间差异的基于Java的操作2的实现可以组合每核每秒大约200K(大小50)直方图(在i7-3615QM上)。这与核心扫描速率不利地相比,查询的计数,总和和组的核心扫描速率高出一个数量级或两个数量级。虽然,公平地说,直方图比单个计数或总和包含1-2个数量级的信息。不过,我们寻求更快的解决方案。如果我们提前知道合并对之下的合适阈值是什么,那么我们可以通过排序对(我们可以在ETL时间做)进行线性扫描,选择是否合并基于阈值。确切地确定该阈值难以有效地进行,但是避免基于堆的解决方案用于该近似导致核心聚合率为~1.3M(大小50)直方图每秒。
索引时我们有3种不同的序列化格式,具体取决于数据的性质,我们使用最有效的编码:
密集格式,存储所有计数和质心,直到可配置的大小参数
稀疏格式,存储一些低于限制的对
紧凑的格式,自己存储各个值
重要的是要强调我们可以分层次地指定不同的准确度级别。当我们索引数据时,上述格式会起作用,将原始数组转换为(计数,质心)对。因为索引是缓慢且昂贵的并且德鲁伊段是不可变的,所以在这个级别上更好地在准确性方面犯错误。因此,我们在索引中指定最多100个(计数,质心)对,这将在查询时允许更大的灵活性,当我们将它们聚合成一些可能不同数量的(计数,质心)对时。
我们使用计数的多余符号位来确定计数> 1的(计数,质心)对是否准确。值(2,1.51)是否表示2个投标价格为1.51,或2unequalbidpricesthataverageto1.51?计数估计的梯形方法没有这样的区别,并将平等地“分散”其不确定性。这对于投标数据的离散的多模态分布特征可能是有问题的。但是,如果知道哪些(计数,质心)对是精确的,我们可以做出更准确的估计。
回想一下,我们的数据通常表现出很高的偏斜度。因为最接近的直方图对被连续地合并直到对的数量足够小,所以剩余的对必然(相对)相隔很远。总结12个价格在.10和6个价格附近12是合乎逻辑的,因为18个价格在.11左右,但由于49个极高价格的影响,我们不会因为价格过高而无法满足价格 - 除非我们对这些异常值特别感兴趣,即。至少,我们希望能够控制我们的“感兴趣的领域” - 我们关心大多数数据还是关注那些少数异常值?因为当我们汇总数百万或数十亿的价值时,即使是最微小的偏差,我们最终也会用一个(计数,质心)对来总结大部分分布。我们的解决方案是定义特殊限制,在此范围内我们保持估算的准确性。这通常可以为我们的直方图可视化设置x轴限制。
准确性
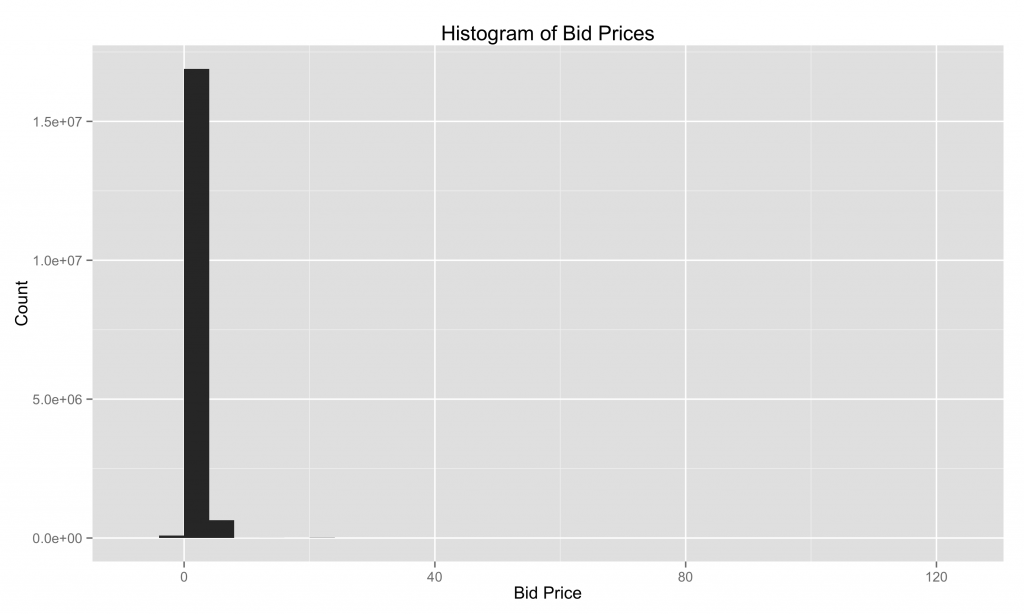
在这里,我们使用x轴限制和箱宽度的默认设置绘制超过~18M价格的直方图。 由于高度偏斜,推断限制不是最理想的,因为它们包括价格~100美元。 此外,甚至还有负价格(这可能是错误的,或者在拍卖中表达不感兴趣的方式)!
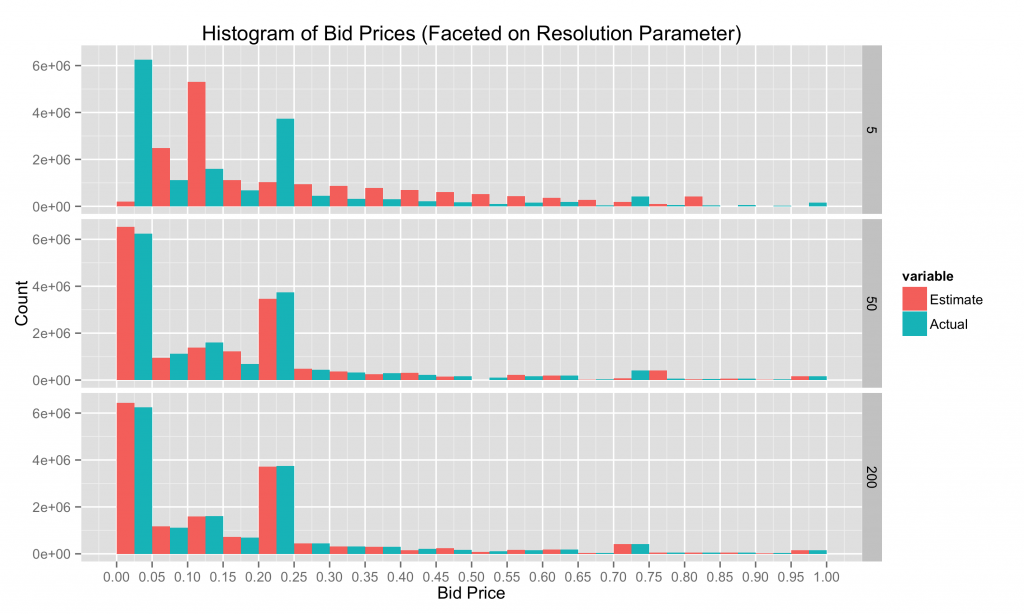
下面,我们将分辨率限制设置为0和1,并在我们的近似直方图数据结构中改变(计数,质心)对的数量。 仅使用5对的准确性非常糟糕,甚至无法捕获.20to.25桶中的第二种模式。 50对票价要好得多,200对非常准确。
速度
让我们看看我们适度的演示集群(4 m2.2xlarge计算节点)上的一些基准测试,其中包含一些维基百科数据。 我们将看看以下聚合器的性能:
计数聚合器,它只计算行数
uniques聚合器,实现HyperLogLog算法的一个版本
近似直方图聚合器,将分辨率从10对改变为50对到200对
我们每周从维基百科获得大约1-3M的汇总数据行,整个32周期间的基准测试覆盖84M行。 查询时间与数据量之间似乎存在大致线性关系:
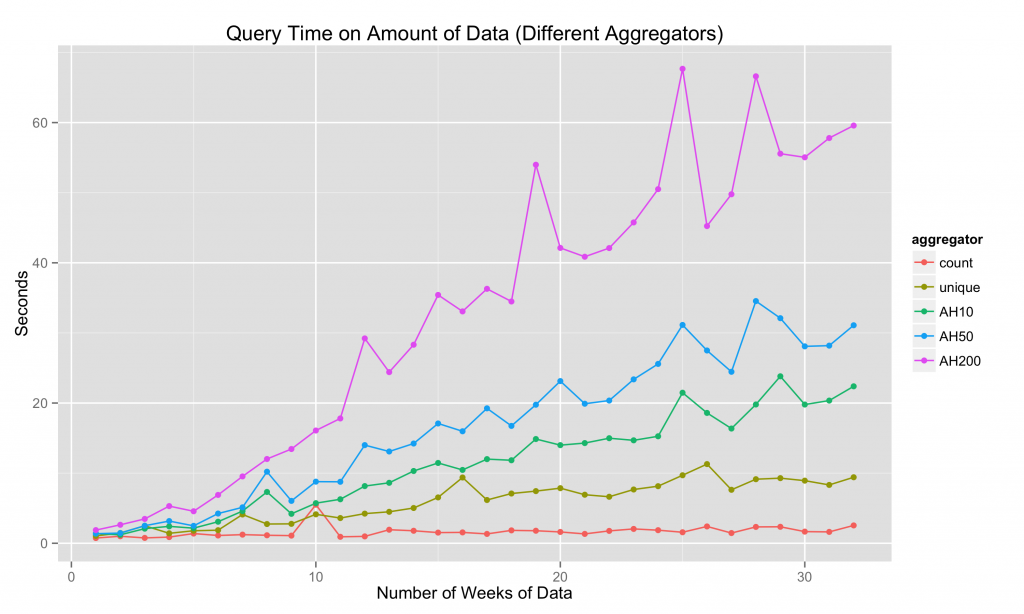
实际上,一旦我们获得足够的数据,群集扫描率往往会趋于平缓:
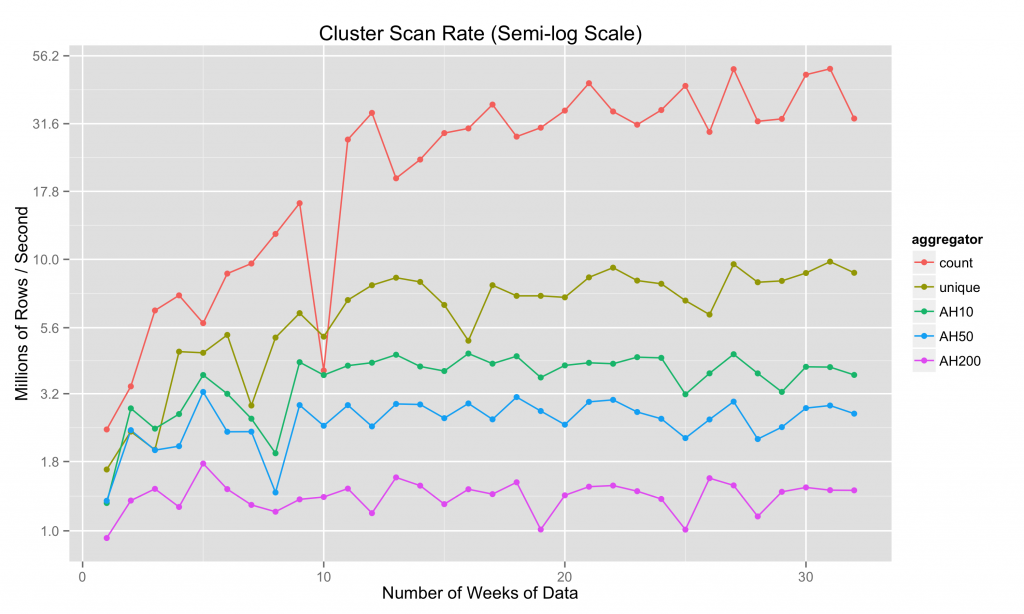
我们以前在更强大的集群上获得了每秒26B行的集群扫描速率。 非常粗略地说,近似直方图聚合器是计数聚合器的速度的1/10,因此我们可以预期在这样的聚类上每秒2-3B行的速度。 回想一下,对于典型的数据集,我们的汇总步骤将10-100行数据压缩为1。 这意味着可以构建直方图,表示数秒到数百亿的价格。
如果您喜欢阅读并且对如何实现更快的速度/准确性/灵活性有所了解,我们建议您加入Metamarkets。
最后,我的同事杨方进和我将于10月份在纽约Strata会议上继续讨论,我们将在会上提出“不完全! 通过近似算法快速查询。“





