数据分析 - numpy-note

目录

• 科学计算库
  • numpy相关介绍
    • 简介
    • 安装与使用
    • 快捷操作
  • 第一部分 基本操作
    • 第一节 数组创建
      • np.array
      • ones - zeros - full
      • arange - linspace - logspace
      • random: randn - randint - random
      • 均匀分布 uniform
    • 第二节 数据查看
      • 形状 - shape
      • 数据类型 - dtype
      • 元素个数 -size
      • 维度 / 轴数 - ndim
      • 每个元素占字节大小 - itemsize
    • 第三节 数据保存 - 文件IO操作
      • 单个文件 - save - load
      • 多个文件 - savez - load
      • csv/txt文件 - savetxt - loadtxt
  • 第二部分 数据类型
    • 整数
    • 浮点数
    • 字符串
    • 转换数据类型 - astype
  • 第三部分 数组运算
    • 算术运算
    • 逻辑运算
    • 数组与标量计算
    • 赋值运算
  • 复制与视图 - 深浅拷贝
    • 完全没有复制 b = a
    • 查看或浅拷贝 - 搞不清楚的时候 - 可用深拷贝
    • 深拷贝
    • 总结
  • 第五部分 索引与切片
    • 基本索引与切片 - 影响原数据
      • 一维数组索引和切片
      • 二维数组索引和切片
    • 花式索引 - 不影响原数据
      • 花式索引技巧 - 整数数组
        • 一维数组
        • 二维数组 之 行、列索引
        • 二维数组之具体位置
        • 按区域取值
      • boolean值索引
    • 总结 - 直接用这个
  • 第六部分 形状操作
    • 数组变形 - reshape/resize
    • 数组转置 - T / transpose
    • 数组堆叠 - concatenate
    • 数组拆分 - split
  • 第七部分 广播机制 - 看图秒懂
    • 一维数组广播
    • 二维数组的广播
    • 三维数组广播
  • 通用函数
    • 元素级别数字函数
      • abs/round/ceil/floor
      • sqrt/squre/power/开幂次方
      • exp/log
      • pi/sin/cos/tan
      • maxinmum/minimum
      • argmax/argmin
      • all/any - 通用判断函数
      • clip - 裁剪
    • unique/set - 去重
    • where函数 -三元运算符
    • 排序方法
      • 关于排序的重要注意事项
      • arr.sort - 改变原数据
      • np.sort - 返回深拷贝的排序结果
      • np/arr.argsort - 返回索引
      • arr/np.argmax/argmin - 返回索引
    • 集合运算
    • 数学和统计函数
      • mean/sum/size
      • max/min
      • argmax/argmin - 最大最小值索引
      • cumsum/cumprod - 累加/累乘
      • cov/corrcoef - 协方差/相关性系数
  • 线性代数 - 矩阵运算
    • 矩阵乘积 - dot/ @
    • 矩阵其他计算
  • 用NumPy分析鸢尾花花萼属性各项指标
  • 玫瑰花颜色调整
  • numpy初级 - 作业1
    • 创建一个长度为10的一维全为0的ndarray对象，然后让第5个元素等于1
    • 创建一个元素为从10到49（包含49）的ndarray对象，间隔是1
    • 将第2题的所有元素位置反转
    • 使用np.random.random创建一个10*10的ndarray对象，并打印出最大最小元素
    • 创建一个10*10的ndarray对象，且矩阵边界全为1，里面全为0
    • 创建一个每一行都是从0到4的5*5矩阵
    • 创建等差数列/等比数列
    • 创建一个长度为10的正态分布数组np.random.randn并排序
    • 创建一个长度为10的随机数组并将最大值替换为-100¶
    • 如何根据第3列大小顺序来对一个5*5矩阵排序？（考察argsort()方法）¶
  • numpy高级 - 作业2
    • 给定一个4维矩阵，如何得到最后两维度的和?
    • 如何得到在找个数组的每个元素之间插入3个0后的新数组
    • 给定一个二维矩阵(5行4列)，如何交换其中两行的元素
    • 创建一个1000000长度的随机数组，使用两种方法求其三次方
    • 创建又给5行3列随机矩阵和3行2列随机矩阵，求矩阵积
    • 矩阵的每一行的元素都减去该行平均值
    • 打印特定矩阵
    • 正则化一个5行5列的随机矩阵
    • 根据两个或多个条件过滤numpy数组

科学计算库

numpy相关介绍

简介

NumPy（Numerical Python）是Python的一种开源的数值计算扩展。提供多维数组对象，各种派生对象（如掩码数组和矩阵），这种工具可用来存储和处理大型矩阵，比Python自身的嵌套列表（nested list structure)结构要高效的多（该结构也可以用来表示矩阵（matrix）），支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库，包括数学、逻辑、形状操作、排序、选择、输入输出、离散傅立叶变换、基本线性代数，基本统计运算和随机模拟等等。

安装与使用

• 几乎所有从事Python工作的数据分析师都利用NumPy的强大功能。

  • 强大的N维数组
  • 成熟的广播功能
  • 用于整合C/C++和Fortran代码的工具包
  • NumPy提供了全面的数学功能、随机数生成器和线性代数功能

• 安装Python库

  • 第一种方式：
  • pip install jupyter -i https://pypi.tuna.tsinghua.edu.cn/simple
  • pip install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple
  • 第二种方式：
    直接安装[anaconda下载(https://www.anaconda.com/products/individual#Downloads)
  • 使用: - win + R - cmd(回车) - jupyter notebook

• 扩展插件
  jupyter扩展插件（推荐安装）

  • pip install jupyter_contrib_nbextensions -i https://pypi.tuna.tsinghua.edu.cn/simple
  • pip install jupyter_nbextensions_configurator -i https://pypi.tuna.tsinghua.edu.cn/simple
  • jupyter contrib nbextension install --user
  • jupyter nbextensions_configurator enable --user
  • 退出，重新进入jupyter notebook就可以了
  • 注意事项:如果安装后不能使用，需要查看你当前jupyter服务是在哪个环境中运行的
  • 若是是conda默认 - conda activate base + 执行上述操作

快捷操作

• 关于jupyter 的相关快捷操作
  • 快捷键执行代码 - ctrl + enter(回车键)
  • 删除代码 - esc(退出编辑模式) + d + d
  • 编辑代码 - enter(在当前cell中回车)
  • 前插 - esc + a
  • 后插 - esc + b
  • 合并 - ctrl + m
  • 转换为md - esc + m

第一部分 基本操作

第一节 数组创建

• 创建数组的最简单的方法就是使用array函数，将Python下的list转换为ndarray。
• 我们可以利用np中的一些内置函数来创建数组，比如我们创建全0的数组，也可以创建全1数组，全是其他数字的数组，或者等差数列数组，正态分布数组，随机数。

np.array

# 使用原生的np.array 方法将 列表或元组 转换为 array类型
import numpy as np
l = [1,3,5,7,9] # 列表
t = (0,2,4,6,8)
# 深拷贝
arr1 = np.array(l)
# 浅拷贝 - 复制索引 - 改变原数据
arr2 = np.asarray(t)

display(arr1,arr2)

ones - zeros - full

import numpy as np

# 全为 1
arr1 = np.ones(shape = (5,5)) # shape 代表创建的维度

# 全为 0
arr2 = np.zeros(shape = 5) # shape 代表创建的维度

# 指定数字
arr3 = np.full(shape= (3,3),fill_value=3.14)

display(arr1,arr2,arr3)

arange - linspace - logspace

import numpy as np

# 等差数列 -0 - 10 - 步长为 2 - 顾头不顾尾
arr4 = np.arange(start = 0,stop = 10, step = 2) 

# 等差数列 - 0 - 10 - 生成11 个数 - 等距离
arr5 = np.linspace(start = 0,stop = 10,num = 11)

# 等比数列 - 0 - 20 - base = 公比 = 2
np.set_printoptions(suppress = True) # 不显示科学技术法
arr6 = np.logspace(start = 0,stop = 10,base = 2,num = 11)

display(arr4,arr5,arr6)

random: randn - randint - random

import numpy as np

# 一维数组 - 正态分布 - 平均值是0 ，标准差是 1
arr7 = np.random.randn(10)

# 二维数组 - int - 0 - 9 - 2 行 3 列
arr8 = np.random.randint(0,10,size = (2,3))

# 三维数组 - flaot - 2 z 3 x 4 y 
arr9 = np.random.random(size=(2,3,4))

display(arr7,arr8,arr9)

均匀分布 uniform

import numpy as np
# 均匀分布  最低为 -1  最高为 1   数量为1000000
data1 =  np.random.uniform(-1,1,1000000)
data1

第二节 数据查看

• shape - 尺寸形状
• dtype - 数据类型
• size - 元素个数
• ndim - 维度
• itemsize - 内存占字节大小

NumPy的数组类称为ndarray，也被称为别名 array。请注意，numpy.array这与标准Python库类不同array.array，后者仅处理一维数组且功能较少。ndarray对象的重要属性是

形状 - shape

import numpy as np
arr = np.random.randint(0,10,size = (2,3,4))

# 尺寸形状
r1 = arr.shape
display(r1)

数据类型 - dtype

import numpy as np
arr = np.random.randint(0,10,size = (2,3,4))
# 数据类型
r2 = arr.dtype
display(r2)

元素个数 -size

import numpy as np
arr = np.random.randint(0,10,size = (2,3,4))
# 元素个数
r3 = arr.size
display(r3)

维度 / 轴数 - ndim

# 维度 - size关键字 - 元组的长度
r4 = arr.ndim
display(r4)

每个元素占字节大小 - itemsize

# 数组中每个元素的大小(以字节为单位) 1 Bytes = 8 bit 
r5 = arr.itemsize # 32/8 = 4
display(r5)

第三节 数据保存 - 文件IO操作

• save方法保存ndarray到一个npy文件，也可以使用savez将多个array保存到一个.npz文件中
• load方法来读取存储的数组，如果是.npz文件的话，读取之后相当于形成了一个key-value类型的变量，通过保存时定义的key来获取相应的array

单个文件 - save - load

import numpy as np
arr = np.arange(0,10,3)

# 保存数据 - 到文件 - 序列化
np.save('data/arr.npy',arr)

# 加载数据 - 从文件中 - 反序列化
load_arr = np.load('data/arr.npy')
display(load_arr)

多个文件 - savez - load

import numpy as np
arr1 = np.arange(0,10,3)
arr2 = [range(0,10,2)]

# 保存数据 - 到文件 - 序列化 - (k - v)
np.savez('data/arr.npz',a1= arr1,a2=arr2 )

# 加载数据 - 从文件中 - 反序列化 - 
load_arr1 = np.load('data/arr.npz')['a1']
load_arr2 = np.load('data/arr.npz')['a2']
display(load_arr1,load_arr2)

csv/txt文件 - savetxt - loadtxt

import numpy as np
arr1 = np.arange(1,10,2)
arr2 = np.arange(0,10,2)
# 保存数据 - 到文件 - 序列化 - (k - v)
np.savetxt('data/arr.csv',arr1,delimiter=',',encoding='utf8' )
np.savetxt('data/arr.txt',arr2,delimiter=';',encoding='utf8')


# 加载数据 - 从文件中 - 反序列化 - 
load_arr1 = np.loadtxt('data/arr.csv')
load_arr2 = np.loadtxt('data/arr.txt')
display(load_arr1,load_arr2)

第二部分 数据类型

• 整数
• 浮点数
• 字符串
• ndarray的数据类型：
  • int: int8、uint8、int16、int32、int64
  • float: float16、float32、float64
  • str

整数

import numpy as np
# 整数 -  8 16 32 64
arr = np.array([2,3,4],dtype=np.int16)
arr.dtype

浮点数

import numpy as np
# 浮点数 - 16 32 64
arr2 = np.array([1,2,3],dtype=np.float32)
arr2.dtype

字符串

# 字符串
import numpy as np
# 浮点数 - 16 32 64
arr3 = np.array(['a','b','c'])
arr3.dtype

转换数据类型 - astype

import numpy as np
# 创建时候 - 指定
arr = np.array([2,3,4],dtype=np.int16)
arr2 = np.array([1,2,3],dtype=np.float32)

# 转换数据类型 - 重新指定
r1 = arr.astype(np.int64)
r2 = arr2.astype(np.float64)

display(r1.dtype,r2.dtype)

第三部分 数组运算

算术运算

import numpy as np
arr1 = np.array([1,2,3,4,5])
arr2 = np.array([2,3,1,5,9])

# 算术运算 - 可数组之间运算 - 也可 单个数组标量运算 
# 数组之间
arr1 + arr2 # 加法
arr1 - arr2 # 减法
arr1 * arr2 # 乘法
arr1 / arr2 # 除法
arr1 // arr2 # 取整
arr1 % arr2 # 取余
arr1 ** arr2 # 两个星号表示幂运算

逻辑运算

import numpy as np
arr1 = np.array([1,2,3,4,5])
arr2 = np.array([1,0,2,3,5])

# 逻辑运算 - 可数组之间运算 - 也可单个数组
# 单个数组 
arr1 < 5 
arr1 >= 5
arr1 == 5

# 数组之间
arr1 == arr2
arr1 > arr2

数组与标量计算

• 数组与标量的算术运算也会将标量值传播到各个元素

import numpy as np
arr = np.arange(1,10)

# 单个数组 - 运用了广播机制 - 可行/列复制
arr1 + 1 # 加法
arr1 - 2 # 减法
arr1 * 3 # 乘法
arr1 / 4 # 除法
arr1 // 5 # 取整
arr1 % 6 # 取余
arr1 ** 7 # 两个星号表示幂运算

赋值运算

• 某些操作（例如+=和*=）只会修改现有数组，而不是创建一个新数组。

import numpy as np
arr1 = np.arange(5)
arr1 +=5
arr1 -=5
arr1 *=5
arr1
# arr1 /=5 不支持运算

复制与视图 - 深浅拷贝

• 在操作数组时，有时会将其数据复制到新数组中，有时不复制。
• 对于初学者来说，这通常会引起混乱。有以下三种情况:
  • 完全没有复制
  • 查看或浅拷贝
  • 深拷贝

完全没有复制 b = a

import numpy as np
a = np.random.randint(0,100,size = (4,5))
b = a
a is b # 返回True a和b是两个不同名字对应同一个内存对象
b[0,0] = 1024 # 命运共同体
display(a,b)

查看或浅拷贝 - 搞不清楚的时候 - 可用深拷贝

不同的数组对象可以共享相同的数据。该view方法创建一个查看相同数据的新数组对象

# 不同的数组对象可以共享相同的数据。
# 该view方法创建一个查看相同数据的新数组对象

# 总结: 浅拷贝 - 切片和索引 - 影响原数据
import numpy as np
a = np.random.randint(0,100,size = (4,5))


# 下面是一个对我来说毫无意义，我也不是很懂的理论方法

b = a.view()  # 使用a中的数据创建一个新数组对象

a is b # 返回False a和b是两个不同名字对应同一个内存对象，值得是第一层对应的内存地址

b.base is a # 返回True，b视图的根数据和a一样 指的是第一层

b.flags.owndata # 返回False b中的数据不是其自己的

b.base.flags.owndata # 返回False b中的数据是自己的

a.flags.owndata # 返回True a中的数据是其自己的

b[0,0] = 1024  # a和b的数据都发生改变
a[1,1] = 2048  # a和b的数据都发生改变

display(a,b)

深拷贝

# 深拷贝:完全与原数据隔离，复制原数据的一切，开辟一片的新的空间
# 总结：索引切片 - 不影响原数据
import numpy as np
a = np.random.randint(0,100,size = (4,5))
b = a.copy()
b is a # 返回False
b.base is a # 返回False
b.flags.owndata # 返回True
a.flags.owndata # 返回True
b[0,0] = 1024 # b改变，a不变，分道扬镳
display(a,b)

总结

• copy应该在不再需要原来的数组情况下，切片后调用。
  • 例如，假设a是一个巨大的中间结果，而最终结果b仅包含的一小部分a，
  • 则在b使用切片进行构造时应制作一个深拷贝：

import numpy as np
a = np.arange(1e8)
b = a[::1000000].copy() # 每100万个数据中取一个数据
del a # 不再需要a，删除占大内存的a
b.shape # shape(100,)

第五部分 索引与切片

基本索引与切片 - 影响原数据

一维数组索引和切片

numpy中数组切片是原始数组的视图，这意味着数据不会被复制，视图上任何数据的修改都会反映到原数组上

# numpy中数组切片是原始数组的视图，这意味着数据不会被复制，视图上任何数据的修改都会反映到原数组上
import numpy as np
arr = np.random.randint(0,100,size = 10)

# 不连续取 - 多个 - 索引 -根据位置取相应数据
r1 = arr[[0,3,5]]

# 连续取 - 切片 - start - end - step - 顾头不顾尾
r2 = arr[3:6]         # 切片 - 从3到6
r3 = arr[3:6:2]       # 从3到6，2表示两个中取一个
r4 = arr[:]           # 默认全部数据
r5 = arr[::-1]        # 倒叙索引
r6 = arr[1:2] = 1024  # 浅拷贝 - 原数据改变

display(r1,r2,r3,r4,r5,arr)

二维数组索引和切片

numpy中数组切片是原始数组的视图，这意味着数据不会被复制，视图上任何数据的修改都会反映到原数组上

# numpy中数组切片是原始数组的视图，这意味着数据不会被复制
# 视图上任何数据的修改都会反映到原数组上
import numpy as np
arr = np.random.randint(0,10,size = (3,5))  # 三行五列
print('原数据:')
display(arr)

print('操作后：')
# 不连续 -多个
r1 = arr[1,[1,2]]     # 第 1 行  -  第 1、2列 数据

r2 = arr[[1,2],1]     # 第 1、2 行 第 1 列 数据

# 连续取 - 多个
r3 = arr[0:2,1:4]  # 取 第1、2行 第 2、3、4列的数据

# 批量修改数据 - 浅拷贝 - 原数据该改变
arr[0:2,1:4] = 1024   # 切片赋值会赋值到每个元素上，与列表操作不同
arr[:] = np.arange(0,5)

display(r1,r2,r3,arr)

花式索引 - 不影响原数据

花式索引技巧 - 整数数组

整数数组进行索引即花式索引,其和切片不一样，它总是将数据复制到新数组中

• 按行
• 按列
• 行列具体取值
• 按区域

一维数组

# 整数数组进行索引即花式索引,其和切片不一样，它总是将数据复制到新数组中
import numpy as np
# 一维数组 - []
print('一维数组：')
arr1 = np.arange(0,10)
display(arr)
arr2 = arr1[[1,3,5,7]]
display(arr2)
arr2[1] = 1024  # 修改值,不影响原数据 arr1
display(arr2)

二维数组 之 行、列索引

import numpy as np
# 二维数组
print('二维数组：')
arr3 = np.random.randint(0,10,size=(5,5))
print('原数组：')
display(arr3)

# 根据行
arr4 =  arr3[[1,3]] # 获取 第2行 + 第4行 数据
print('按行取：')
display(arr4) 

# 根据列
arr5 =  arr3[:,[0,2]]   # 获取 第1列 + 第3列 数据
print('按列取：')
display(arr5) 

二维数组之具体位置

import numpy as np
# 二维数组
print('二维数组：')
arr3 = np.random.randint(0,10,size=(5,5))
print('原数组：')
display(arr3)

# 根据行/列取值 - 具体值
print('按行列取：arr3[([1,3],[0,2])]')
arr6 = arr3[([1,3],[0,2])] # 获取 第2行第1列  + 第4行第3列 数据
arr6 = arr3[[1,3],[0,2]] # 不写元组也行
display(arr6) 

按区域取值

import numpy as np
# 二维数组
print('二维数组：')
arr3 = np.random.randint(0,10,size=(5,5))
print('原数组：')
display(arr3)

# 选择一个区域
# 第一个列表存的是待提取元素的行标，第二个列表存的是待提取元素的列标
print('选择一片区域：arr3[[1,3,3,3]][:,[2,4,4]]')

arr7 = arr3[[1,3,3,3]][:,[2,4,4]]
arr8 = arr3[np.ix_([1,3,3,3],[2,4,4])] # ix_()函数可用于组合不同的向量

display(arr7,arr8) 

boolean值索引

# 布尔索引 - 以array列表返回True或False
import numpy as np

# 取出 x > 6
arr = np.arange(0,10)
arr
cond1 = arr > 6
r1 = arr[cond1]

# 取出 3 < x < 8 - 条件用括号 - 不然不匹配
cond2 = ( arr > 3 ) & (arr < 8)
r2 = arr[cond2]

# 取出 3>x 或 x>8
cond3_1 =  arr < 3
conn3_2 =  arr > 8
cond3 = cond3_1 | conn3_2
r3 = arr[cond3]

display(r1,r2,r3)

总结 - 直接用这个

# 其实无论是基本索引还是花式索引，都是为了取值，那么既然为了取值，何必要搞得这么复杂呢
# 故做出以下简单总结，方便快速使用:
import numpy as np
arr = np.random.randint(0,10,size=(5,5))
# 方法一 切片和索引 - 只分左右 - 重新赋值
arr[1:3,1:2]
arr[:,[1,3]]
arr[[1,4],:] # arr[[1,4]]  都是获取行，何必搞得那么麻烦呢
# 方法二 具体值 - 列表 -长度相等 - 一一对应
arr[[1,2,3,4],[1,2,3,4]]
# 方法三 选定区域 - 列表取值
arr7 = arr[[1,2,3]][:,[1,2,3]]
arr8 = arr[np.ix_([1,2,3],[1,2,3])] # ix_()函数可用于组合不同的向量

第六部分 形状操作

• 数组重塑 - reshape/resize
• 数组转置 - T /tanspose
• 数组堆叠 - concatenate
• 数组拆分 - split

数组变形 - reshape/resize

• reshape 改变数组的形状
• resize 改变了数据 - 没有返回值

import numpy as np

# 数组变形 - reshape - 注意:变形后的数据，要与原数组的元素个数对得上，且每行列要相等

arr1 = np.random.randint(0,10,size = (3,2,1))

arr2 = arr1.reshape(3,2) # 形状改变，返回新数组

arr3 = arr1.reshape(-1,1) # 自动“整形”，自动计算
arr4 = arr1.reshape(1,-1) # 自动“整形”，自动计算

arr5 = arr1.copy()
arr5.resize(3,2)
display(arr1,arr2,arr3,arr4,arr5)

数组转置 - T / transpose

import numpy as np

# 数组转置 - T
arr1 = np.random.randint(0,10,size = (3,5)) # shape(3,5)
arr2 = arr1.T                              # shape(5,3) 转置

display(arr1,arr2)

# 数组转置 - transpose - axes - 表示的是以前的维度  - 0   1  2 ...
arr3 = np.random.randint(0,10,size = (2,3,4)) # shape(2, 3, 4)
arr4 = np.transpose(arr3,axes=(2,0,1))        # transpose改变数组维度 shape(4, 2, 3)
display(arr3.shape,arr4.shape)

数组堆叠 - concatenate

• vstack - 按照行堆叠
• hstack - 按照列堆叠
• 其实在这里，有疑惑的是，为什么用法效果是相反的呢？
• 其实想想看，
  • vstack 是将数据竖直放下去
  • hstack 是将数据水平放下去
• axis = 0 从最后一行添加
• axis = 1 从最后一列添加

# 数组堆叠 - 就是对多个数组的合并 
# - 可以按行合并  - 也可按列合并
# 推荐使用concatenate + axis 
import numpy as np

# 按行堆叠 - 竖直方向 - 添加在最后一行后面
print('按行堆叠 - 原数据：')
arr1 = np.random.randint(0,10,size = (1,4))
arr2 = np.random.randint(-10,0,size = (1,4))
display(arr1,arr2)

print('按行堆叠后：')
r1 = np.concatenate([arr1,arr2,arr1],axis=0)
r2 = np.vstack((arr1,arr2))
display(r1,r2)

# 按列堆叠 - 水平方向 - 条件在最后一列后面
print('按列堆叠 - 原数据：')
arr3 = np.random.randint(0,10,size = (3,2))
arr4 = np.random.randint(-10,0,size = (3,3))
display(arr3,arr4)

print('按列堆叠后：')
r3 = np.concatenate([arr3,arr4],axis = 1)
r4 = np.hstack((arr3,arr4)) 
display(r3,r4)

数组拆分 - split

# split数组拆分 - 可行可列 - 基本等分
# 避坑 - 行/列 要被拆分数整除 - (ary, indices_or_sections, axis=0)
# 推荐使用split + axis 

import numpy as np
arr = np.random.randint(0,10,size = (4,4)) 
print('原数据：')
display(arr)

# 按行拆分 - 竖直方向
r1 = np.split(arr,2,axis=0) # 平均分
r2 = np.vsplit(arr,[1,3]) # 在水平方向，以索引1，3为断点分割成3份
print('按行拆分：')
display(r1,r2)

# 按列拆分 - 水平方向
r3 = np.split(arr,[1,3],axis=1) # 在竖直方向，以索引1，3为断点分割成3份
r4 =  np.hsplit(arr, 2)
print('按列拆分：')
display(r3,r4)

# np.split(arr,indices_or_sections=2,axis = 0) # 在第一维（6）平均分成两份 
# np.split(arr,indices_or_sections=[2,3],axis = 1) # 在第二维（5）以索引2，3为断点分割成3份

# np.vsplit(arr,indices_or_sections=3) # 在竖直方向平均分割成3份
# np.hsplit(arr,indices_or_sections=[1,4]) # 在水平方向，以索引1，4为断点分割成3份

第七部分 广播机制 - 看图秒懂

当两个数组的形状并不相同的时候，我们可以通过扩展数组的方法来实现相加、相减、相乘等操作，这种机制叫做广播（broadcasting）

一维数组广播

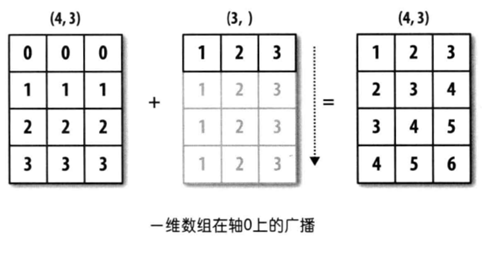
# 当两个数组的形状并不相同的时候，
# 我们可以通过扩展数组的方法来实现相加、相减、相乘等操作，
# 这种机制叫做广播（broadcasting）
# 注意事项：必须要 行或列 对其

# 一维数组的广播 - 向下复制 - 只有1行
import numpy as np
arr1 = np.sort(np.array([0,1,2,3]*3)).reshape(4,3) # shape(4,3)
arr2 = np.array([1,2,3])                           # shape(3,)

display(arr1,arr2)

arr3 = arr1 + arr2 # arr2进行广播复制4份 shape(4,3)
arr3

二维数组的广播

# 二维数组的广播 - 向右复制 - 只有1列
import numpy as np
arr1 = np.sort(np.array([0,1,2,3]*3)).reshape(4,3) # shape(4,3)
arr2 = np.array([1,2,3,4]).reshape(4,1)               # shape(4,1)

display(arr1,arr2)

arr3 = arr1 + arr2                               # arr2 进行广播复制3份 shape(4,3)
arr3

三维数组广播

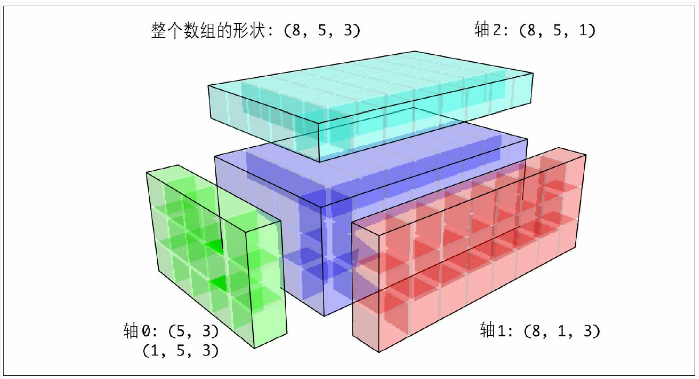
import numpy as np
arr1 = np.array([0,1,2,3,4,5,6,7]*3).reshape(3,4,2) #shape(3,4,2)
arr2 = np.array([0,1,2,3,4,5,6,7]).reshape(4,2) #shape(4,2)
arr3 = arr1 + arr2 # arr2数组在0维上复制3份 shape(3,4,2)
arr3

通用函数

元素级别数字函数

abs、sqrt、square、exp、log、sin、cos、tan，maxinmum、minimum、all、any、inner、clip、round、trace、ceil、floor

abs/round/ceil/floor

import numpy as np
arr1 = np.random.randint(-10,11,size=(4,4))
arr2 = arr1 + np.random.random(size=4)

# 绝对值 - abs
r1 = np.abs(arr1)
display(r1)

# 四舍五入 - round
r1 = np.round(arr2)
display(r1)

# 向上取整
r1 = np.ceil(arr2)
display(r1)

# 向下取整
r1 = np.floor(arr2)
display(r1)

sqrt/squre/power/开幂次方

import numpy as np
# 开方 - 标准差
r2= np.sqrt(4)
display(r2)

# 平方 
r2 = np.square(4)
display(r2)

# 幂次方
r2 = np.power(2,10)
r3 = 2 ** 10
display(r2,r3)

# 开幂方根
def func(x,i):
    return x ** (1/i)
r3 = func(8,3)
display(r3)

exp/log

import numpy as np
# exp 自然底数
r4 =  np.exp
r5 =  np.e
display(r4,r5)

# log 底数函数
r5 =  np.log2(8)
display(r5)

pi/sin/cos/tan

import numpy as np
# 圆周率Π
r6 = np.pi
display(r6)

# sin/cos/tan
r6 = np.sin(np.pi/3)
r7= np.cos(np.pi/3)
r8 = np.tan(np.pi/3)
display(r6,r7,r8)

maxinmum/minimum

# 比较最大最小值 - 并返回结果
import numpy as np
arr1 = np.random.randint(-10,11,size=(4,4))
arr2 = arr1 + np.random.randint(-1,1,size=4)
arr3 = np.arange(0,10)
# maxinmum  - 比较数组之间的最大值 - argmax(返回索引)b
r9 = np.maximum(arr1,arr2)
display(r9)

# minimum - 比较数组之间的最小值 - argmin(返回索引)
r9 = np.minimum(arr1,arr2)
display(r9)

argmax/argmin

# 比较最大最小值 - 并返回结果
import numpy as np
arr1 = np.random.randint(-10,11,size=(4,4))
arr2 = arr1 + np.random.randint(-1,1,size=4)
arr3 = np.arange(0,10)
# argmax(返回索引) - 可按照行列 - axis = 0 - 列
r9 = arr1.argmax(axis=0)
display(r9)

# margmin(返回索引) - - 可按照行列 -  axis = 1 - 行
r9 = arr2.argmin(axis=1)
display(r9)

all/any - 通用判断函数

import numpy as np
arr1 = np.random.randint(-10,11,size=(4,4))
arr2 = arr1 + np.random.randint(-1,1,size=4)
arr3 = np.arange(0,10)

# all - 全真才真,有假就假
cond1 = arr3 > 6
r9 = np.all(cond1)
display(r9)

# any - 有真就真，全假才假
cond2 = arr3 > 0
r9 = np.any(cond2)
display(r9)

clip - 裁剪

import numpy as np
arr1 = np.arange(0,10)

# clip - 裁剪 - 小于 3 -> 3 大于8 ->8
r10 = np.clip(arr1,3,8)
display(r10)
b

unique/set - 去重

import numpy as np
# 数据去重 - set其实可以去重，但是是无序的
arr = np.array([1,2,3,4,5,4,3,2,1])
data1 = np.unique(arr)
display(data1)
set(arr)

where函数 -三元运算符

where 函数，三个参数，条件为真时选择值的数组，条件为假时选择值的数组

# where 函数，三个参数，条件为真时选择值的数组，条件为假时选择值的数组
# 相当于 if else的用法
import numpy as np
arr1 = np.array([1,3,5,7,9])
arr2 = np.array([2,4,6,8,10])

# 数组之间比较
r1 = np.where(arr1 > arr2,arr1,arr2) # 符合返回arr1 不符合返回arr2

# 单个数组比较
cond1 =  arr1 > 3
conn2 =  arr1 < 8
cond3 = cond1 & conn2

r2 = np.where(cond3,True,False) # 符合返回arr1 不符合返回5

display(r1,r2)

排序方法

np中还提供了排序方法，排序方法是就地排序，即直接改变原数组

• arr.sort() - 改变原数组
• np.sort() - 不改变原数组，返回排序结果
• arr.argsort() - 不改变原数组，返回排序索引
• axis(必须要理解含义)
  • axis - 实际代表的是维度
  • 比如三维数组:(2,3,4):
    • axis = 0 <-> 2 倒叙 - 3
    • axis = 1 <-> 3 倒叙 -2
    • axis = 2 <-> 4 倒叙 -1
  • 对应关系:
    • 0:对四维排序 1 :对三维排序 2:对列排序 3:对行排序
    • -1:对行排序 -2:对列排序 -3:对三维排序 -4:对四维排序

关于排序的重要注意事项

# 注意点 - 按对每行排序 - 列  对每列排序 - 行

# 给定一个4维矩阵，如何得到最后两维度的和?
import numpy as np
arr = np.random.randint(0,10,size = (2,3,4,5))
arr
# 0:对四维排序  1 :对三维排序  2:对列排序   3:对行排序
# -1:对行排序  -2:对列排序   -3:对三维排序 -4:对四维排序
arr.sum()
arr.sum(axis = (-1,-2))
arr.sum(axis = (0,1))

arr.sort - 改变原数据

import numpy as np
arr1=np.random.randint(0,10,size=(2,3,4))
# arr1 = np.array([9,3,11,6,17,5,4,15,1])
arr2 = arr1.copy()
print('原数据：')
display(arr1)

print('arr.sort 排序结果 :')
# arr.sort  - 直接改变原数组  - 不返回深拷贝排序结果 
r1 = arr1.sort()
display(arr1,r1)

np.sort - 返回深拷贝的排序结果

import numpy as np
arr1=np.random.randint(0,10,size=(2,3,4))
# arr1 = np.array([9,3,11,6,17,5,4,15,1])
arr2 = arr1.copy()
print('原数据：')
display(arr1)

print('np.sort:')
#  np.sort  - 不改变原数组 - 返回深拷贝排序结果
r2 = np.sort(arr2,axis=2)
print('原数据排序后未改变:')
display(arr2)
print('排序结果:')
display(r2)

np/arr.argsort - 返回索引

import numpy as np
arr1=np.random.randint(0,10,size=(2,3,4))
# arr1 = np.array([9,3,11,6,17,5,4,15,1])
arr2 = arr1.copy()
print('原数据：')
display(arr1)

print('np/arr.argsort 排序结果:')
# arr.argsort -不改变原数组 -  返回从小到大排序索引 
r3 = np.argsort(arr2)   # arr2.argsort()

display(arr2,r3)

print('arr/np.argmax/argmin 排序结果:')
# 补充
r4 = np.argmax(arr2)
r5 = arr2.argmin()
display(r4,r5)

arr/np.argmax/argmin - 返回索引

import numpy as np
arr1=np.random.randint(0,10,size=(2,3,4))
# arr1 = np.array([9,3,11,6,17,5,4,15,1])
arr2 = arr1.copy()
print('原数据：')
display(arr1)

print('arr/np.argmax/argmin 排序结果:')
# 补充
r4 = np.argmax(arr2)
r5 = arr2.argmin()
display(r4,r5)

集合运算

• 交集 - intersect1d
• 并集 - union1d
• 差集 - setdiff1d

import numpy as np
A = np.array([2,4,6,8])
B = np.array([3,4,5,6])
print('原数据')
display(A,B)

# 交集 A，B 相同部分 A & B
print('交集:')
r1 = np.intersect1d(A,B) # array([4,6])
display(r1)

# 并集 A，B的全部  A | B
print('并集:')
r2 = np.union1d(A,B) # array([2, 3, 4, 5, 6, 8])

display(r2)

# 差集 A中有，B中没有  A - B 
print('差集:')
r3 = np.setdiff1d(A,B) # array([2, 8])
display(r3)

# 补充:
# 数据去重 - unique
C = np.array([1,2,3,4,5,3,4,2])
r1 = np.unique(C)
print('去重:')
display(r1)

数学和统计函数

min、max、mean、median、sum、std、var、cumsum、cumprod、argmin、argmax、argwhere、cov、corrcoef

mean/sum/size

import numpy as np
arr1 = np.array([[1,2,3],[4,5,6],[7,8,9]])
print('原数据:')
display(arr1)

# 统计数量 - size
r1 = arr1.size
r2 = np.size(arr1,axis=0) # 每列的数量
r3 = np.size(arr1,axis=1) # 每行的数量
print('数量:')
display(r1,r2,r3)

# 计算平均值 - mean
r1 = arr1.mean()        # # 数组的平均值
r2 = np.mean(arr1,axis=0) # 每列的平均值
r3 = np.mean(arr1,axis=1) # 每行的平均值
print('平均值:')
display(r1,r2,r3)

# 计算总和 - sum
r1 = arr1.sum()        # # 数组的总和
r2 = np.sum(arr1,axis=0) # 每列的总和
r3 = np.sum(arr1,axis=1) # 每行的总和
print('总和:')
display(r1,r2,r3)

max/min

import numpy as np
arr1 = np.array([[1,2,3],[4,5,6],[7,8,9]])
print('原数据:')
display(arr1)

# 计算最大值 - max
r1 = arr1.max() # 数组的最大值
pass2 = np.max(arr1,axis=0) # 每列的最大值
r3 = np.max(arr1,axis=1) # 每行的最大值
print('最大值:')
display(r1,r2,r3)

# 计算最小值 - min
r1 = arr1.min() # 数组的最小值
r2 = np.min(arr1,axis=0) # 每列的最小值
r3 = np.min(arr1,axis=1) # 每行的最小值
print('最小值:')
display(r1,r2,r3)

argmax/argmin - 最大最小值索引

import numpy as np
arr1 = np.array([[1,2,3],[4,5,6],[7,8,9]])
print('原数据:')
display(arr1)
# argmax - 计算最大值/最小值的索引 - 可行可列
r1 = arr1.argmax() 
r2 = arr1.argmin()
print('最大/小值索引:')
display(r1,r2)

# argwhere - 返回符合条件的索引
r1 = np.argwhere(arr1 > 6) 
print('符合条件索引:')
display(r1)

cumsum/cumprod - 累加/累乘

# cumsum - 计算累加和
r1 = np.cumsum(arr1)
# cumprod - 计算累乘
r2 = np.cumprod(arr1)
print('计算累加/累乘车结果:')
display(r1,r2)

cov/corrcoef - 协方差/相关性系数

# 计算协方差矩阵/相关性系数 cov/corrcoef
r1 = np.cov(arr2,rowvar=True) # 协方差矩阵
r2 = np.corrcoef(arr2,rowvar=True) # 相关性系数
display(r1,r2)

# 为每一行数据赋值
arr2 = np.random.randint(0,10,size = (4,5))
arr3 = np.arange(1,6)
arr2[:] = arr3
display(arr2)

线性代数 - 矩阵运算

矩阵乘积 - dot/ @

• 矩阵运算 A的最后一维和B的第一维必须一致
• A(m,n) * B(n,l) = C(m,l)

#矩阵的乘积  矩阵运算 A的最后一维和B的第一维必须一致
# 注意 
A = np.array([[4,2,3],
              [1,3,1]]) # shape(2,3)
B = np.array([[2,7],
              [-5,-7],
              [9,3]]) # shape(3,2)

r1 = 4*2 + 2*(-5) + 3*9 
r2 = 4*7 + 2*(-7) + 3*3 
r3 = 1*2 + 3*(-5) + 1*9
r4 = 1*7 + 3*(-7) + 1*3
print('矩阵运算 - 手动:\n',np.array( [[r1,r2],[r3,r4]]))  #矩阵运算 A的最后一维和B的第一维必须一致
print('矩阵运算 - @:\n',A @ B) # 矩阵运算 A的最后一维和B的第一维必须一致
print('矩阵运算 - 点乘- A.dot(B):\n', A.dot(B)) # 矩阵运算 A的最后一维和B的第一维必须一致
print('矩阵运算 - 点乘- np.dot(A,B)):\n', np.dot(A,B)) # 矩阵运算 A的最后一维和B的第一维必须一致

矩阵其他计算

下面可以计算矩阵的逆、行列式、特征值和特征向量、qr分解值，svd分解值

#计算矩阵的逆 - 矩阵是二维 - 且 行数 = 列数
from numpy.linalg import inv,det,eig,qr,svd
A = np.array([[1,2,3],
              [2,3,4],
              [4,5,8]]) # shape(3,3)
display(inv(A)) # 逆矩阵
display(det(B)) # 行列式
display(eig(A)) # 特征向量
display(qr(A))  # qr分解值
display(svd(A)) # svd分解值

# 计算行列式 
from numpy.linalg import inv,det,eig,qr,svd
r1 = det(A @ B) # A * A **(-1) = 1
display(r1)

用NumPy分析鸢尾花花萼属性各项指标

# 用NumPy分析鸢尾花花萼属性各项指标
import numpy as np  # 导入类库 numpy
# data = np.loadtxt('data/iris.csv',delimiter = ',')  # 读取数据文件，data是二维的数组
# data.sort(axis = -1)  # 简单排序
# 从机器学习库中，获取鸢尾花数据集
from sklearn import datasets
iris_obj = datasets.load_iris()

np.savetxt('data/iris.csv',iris_obj.data)
data = np.loadtxt('data/iris.csv')
data.sort(axis = -1) 
print('简单排序后：', data) # 简单排序
print('数据去重后：', np.unique(data)) # 去除重复数据
print('数据求和：', np.sum(data))  # 数组求和
print('元素求累加和', np.cumsum(data))  # 元素求累加和
print('数据的均值：', np.mean(data))  # 均值
print('数据的标准差：', np.std(data))  # 标准差
print('数据的方差：', np.var(data))  # 方差
print('数据的最小值：', np.min(data))  # 最小值
print('数据的最大值：', np.max(data))  # 最大值

玫瑰花颜色调整

import numpy as np
import matplotlib.pyplot as plt
img = plt.imread('data/rose.jpg')
# img.shape # 高、宽度、颜色:红绿蓝
plt.imshow(img)

# 高、宽度、颜色:蓝绿红
plt.imshow(img[:,:,::-1])

# 高、宽度、颜色:蓝绿红
plt.imshow(img[:,:,[1,0,2]])

numpy初级 - 作业1

创建一个长度为10的一维全为0的ndarray对象，然后让第5个元素等于1

# 创建一个长度为10的一维全为0的ndarray对象，然后让第5个元素等于1
import numpy as np
arr = np.zeros(shape=10)
arr[4] = 1
arr

创建一个元素为从10到49（包含49）的ndarray对象，间隔是1

# 创建一个元素为从10到49（包含49）的ndarray对象，间隔是1
import numpy as np
arr = np.arange(10,50,1)
arr

将第2题的所有元素位置反转

# 将第2题的所有元素位置反转
import numpy as np
arr1 = np.arange(10,50,1)
# 反转
arr2 = arr1[::-1]
display(arr1,arr2)

使用np.random.random创建一个10*10的ndarray对象，并打印出最大最小元素

# 使用np.random.random创建一个10*10的ndarray对象，并打印出最大最小元素
import numpy as np
arr = np.random.random(size=(10,10))
display(arr)
r1 = arr.max()
r2 = arr.min()
display(r1,r2)

创建一个10*10的ndarray对象，且矩阵边界全为1，里面全为0

# 创建一个10*10的ndarray对象，且矩阵边界全为1，里面全为0
import numpy as np
# 方式一
arr1 = np.full(shape=(10,10),fill_value=1)
arr1[1:-1,1:-1] = 0
display(arr1)
# 方式二
arr2 = np.zeros(shape=(10,10))
arr2[[0,-1]] = 1
arr2[:,[0,-1]] = 1
display(arr2)

创建一个每一行都是从0到4的5*5矩阵

# 创建一个每一行都是从0到4的5*5矩阵
import numpy as np
arr = np.zeros(shape=(5,5))
arr2 = np.arange(0,5)
arr3 = arr.copy()

# 按照行
arr[:] = arr2
display(arr)

# 使用广播机制
arr3 += arr2
display(arr3)

创建等差数列/等比数列

# 创建一个范围在(0,1)之间的长度为12的等差数列，
# 创建[1,    2,    4,    8,   16,   32,   64,  128,  256,  512, 1024]等比数列。
# 等差数列
arr1 = np.linspace(0,1,12)
arr2 = np.arange(0,1+1/11,1/11)
display(arr1,arr2)
# 等比数列
arr3 = np.logspace(0,10,base=2,num=11,dtype='int32')
display(arr3)

创建一个长度为10的正态分布数组np.random.randn并排序

# 创建一个长度为10的正态分布数组np.random.randn并排序
arr1 = np.random.randn(10)
arr2 = np.sort(arr1)
display(arr1,arr2)

创建一个长度为10的随机数组并将最大值替换为-100¶

# 创建一个长度为10的随机数组并将最大值替换为-100
import numpy as np
arr = np.random.randint(0,10,size=10)
display(arr)
index = np.argmax(arr)
arr[index] = -100
display(arr)

如何根据第3列大小顺序来对一个5*5矩阵排序？（考察argsort()方法）¶

# 如何根据第3列大小顺序来对一个5*5矩阵排序？（考察argsort()方法）
import numpy as np
arr = np.random.randint(0,10,size=(5,5))
display(arr)
# 对第三列数据，进行排序，获取其排序索引
r_sort = np.argsort(arr[:,2])
display(r_sort)  

# 然后通过索引取值
arr2 = arr[r_sort]
display(arr2)

numpy高级 - 作业2

给定一个4维矩阵，如何得到最后两维度的和?

# 给定一个4维矩阵，如何得到最后两维度的和?
import numpy as np
arr = np.random.randint(0,10,size = (2,3,4,5))
arr

# 0:对四维排序  1 :对三维排序  2:对列排序   3:对行排序
# -1:对行排序  -2:对列排序   -3:对三维排序 -4:对四维排序
arr.sum()
arr.sum(axis = (-1,-2))
arr.sum(axis = (0,1))

如何得到在找个数组的每个元素之间插入3个0后的新数组

# 给定一维数组[1,2,3,4,5],
# 如何得到在找个数组的每个元素之间插入3个0后的新数组
import numpy as np
arr1 = np.array([1,2,3,4,5])
arr2 = np.zeros(shape=17,dtype=np.int16)
display(arr1,arr2)
# 有间隔的，取出数据并进行替换 - 使用步长
arr2[::4] = arr1
display(arr2)

给定一个二维矩阵(5行4列)，如何交换其中两行的元素

# 给定一个二维矩阵(5行4列)，如何交换其中两行的元素
import numpy as  np
arr1 = np.random.randint(0,10,size=(5,4))
display(arr1)

# 交换行
arr2 = arr1[[4,3,2,1,0]] 
display(arr2)

# 交换列
arr3 = arr1[:,[3,2,1,0]] 
display(arr3)

创建一个1000000长度的随机数组，使用两种方法求其三次方

# 创建一个1000000长度的随机数组，使用两种方法求其三次方
# (1、for循环 2、numpy自带方法)，比较耗时

# 方法一 - for循环 - 原生
def func1():
    import time
    import random
    t1 = time.time()
    # 迭代器
    # a = (random.randint(0,10) for i in range(1000000))
    # 列表
    a = [random.randint(0,10) **3  for i in range(1000000)]
    t2 = time.time()
    display(t2 - t1)

# 方法二 numpy方法
def func2():
    import time
    t1 = time.time()
    # 迭代器
    # a = (random.randint(0,10) for i in range(1000000))
    # 列表
    b = np.random.randint(0,10,size = 1000000)
    np.power(b,3)
    t2 = time.time()
    display(t2 - t1 )

print('原生方法：')
func1()
print('numpy方法：')
func2()

创建又给5行3列随机矩阵和3行2列随机矩阵，求矩阵积

# 创建5行3列随机矩阵和3行2列随机矩阵，求矩阵积
# 问以在于  (5,3)  (3,2)  A的列要与B的行维度要相同
import numpy as np
A = np.random.randint(0,10,size=(5,3))
B = np.random.randint(0,10,size=(3,2))

# 调用numpy函数dot
r1 = np.dot(A,B)
# 调用对象方法dot
r2 = A.dot(B)
# 使用符号运算
r3 = A @ B

display(r1,r2,r3)

矩阵的每一行的元素都减去该行平均值

# 矩阵的每一行的元素都减去该行平均值
# (注意:计算式指定axis，以及减法操作时，形状改变)
import numpy as np

x = np.random.randint(0,10,size=(3,5))
display(x)

# 获取每一行的平均值
y = x.mean(axis = 1)

# 然后改变形状做减法 - 行转列
# (-1,1) -1 代表最后算，1代表只有1列
r1 = x - y.reshape(-1,1) 
r1

打印特定矩阵

# 打印特定矩阵
import numpy as np
arr = np.zeros(shape=(8,8))
display(arr)

# 对奇数行，的偶数列进行修改 - 下标从零开始
arr[::2,1::2] =1

# 对偶数行，的奇数列 进行修改 - 下标从零开始
arr[1::2,::2] =1

display(arr)

正则化一个5行5列的随机矩阵

\(\rm{ A = \frac{A - A.min}{A.max - A.min}}\)

# 正则化一个5行5列的随机矩阵(数据统一变成0-1之间的数字，相当于进行缩小)
# 正则的概念:矩阵A中的
# 每一个列减去这一列最小值，
# 除以每一个列的最大值减去每一列的最小值

import numpy as np
A = np.random.randint(1,10,size=(5,5))
display(A)

# 根据公示进行计算，注意axis，要真确指定
B = A - A.min(axis=0) / A.max(axis=0) - A.min(axis=0)
display(B)

根据两个或多个条件过滤numpy数组

# 如何根据两个或多个条件过滤numpy数组。
# 加载鸢尾花数据，根据第一列小于5.0 并且第3列大于1.5作为条件筛选数据
import numpy as np
from sklearn import datasets
iris_obj = datasets.load_iris()

np.savetxt('data/iris.csv',iris_obj.data)
iris = np.loadtxt('data/iris.csv')

cond = (iris[:,0] < 5) & (iris[:,2] > 1.5)
r1 = iris[cond]
display(r1)

# 计算鸢尾花数据每一行的softmax的得分 (exp表示自然底数e的幂运算)
np.exp(2) # 幂运算  e = 2.718
np.e ** 2
arr = np.array([2,1,0,1])
display(arr)
exp = np.exp(arr)
(exp / exp.sum()).round()

# 二维
arr = np.array([[1,1,1],[2,2,2],[3,3,3]])
np.exp(arr)

import numpy as np
from sklearn import datasets
iris_obj = datasets.load_iris()

np.savetxt('data/iris.csv',iris_obj.data)
iris = np.loadtxt('data/iris.csv')
# display(iris)

def softmax(x):
    # 对每个数进行求 e ** x
    exp = np.exp(x)
    # 每一行求和，并且进行形状改变(变成二维，可以进行广播)
    res = exp/exp.sum(axis=1).reshape(-1,1)
    return res.round(3)

result = softmax(iris)
print('softmax得分：\n',result[:5])