1.思维导图。
2.重要概念。
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。它具有以下的特点:
每个节点(node)有零个或多个子节点;
没有父节点的节点称为根节点;
每一个非根节点有且只有一个父节点;
除了根节点外,每个子节点可以分为多个不相交的子树;
相关概念:
节点的度:一个节点含有的子树的个数称为该节点的度;
树的度:一棵树中,最大的节点的度称为树的度;
树的种类
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
二叉树:每个节点最多含有两个子树的树称为二叉树;
完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树;满二叉树:对于上述的完全二叉树,如果去掉其第d层的所有节点,那么剩下的部分就构成一个满二叉树(此时该满二叉树的深度为d-1);
霍夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树;
树的遍历:
先序遍历:ABDEC
中序遍历:DBEAC
后序遍历:DEBCA
查找算法:
二分查找:主要是利用了树查找的思想,所以时间复杂度为树的深度,树的深度性质:具有n个结点的完全二叉树的深度为[log2n] + 1,由此导出二分查找的时间复杂度为O(logn),最好的情况就是O(1),刚好就在mid位置。
哈希查找:如果没有碰撞的时候,时间复杂度为O(1),当数字发生全部碰撞时,有最差时间复杂度为O(n)
平衡二叉树:平衡二叉树,是一种二叉排序树,平衡是因为它的每一个结点的左子树和右子树的高度差至少等于1。
由于二叉排序树在非平衡状态时的时间复杂度是O(n),最好的时候就是O(logn),而平衡二叉树就是为了解决二叉排序树的非平衡而产生的忙所以它的查找,插入,删除的时间复杂度都为O(logn)
三。疑难问题
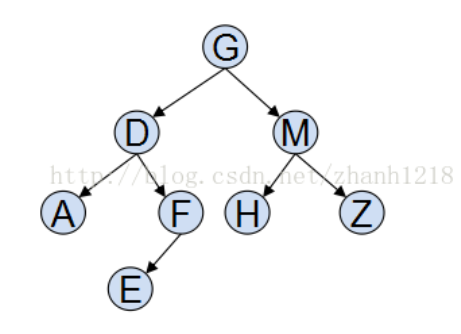
①根据前序遍历特征,我们知道根结点必在首位置,所以为G;
②根据中序遍历特征。其中根节点G左侧的ADEF必然是根节点的左子树,G右侧的HMZ必然是根节点的右子树;
③根据前序中序特征,重复以上步骤。递归找到子树根节点;
那么,我们可以画出这个二叉树: