集合---------------构造，状压dp
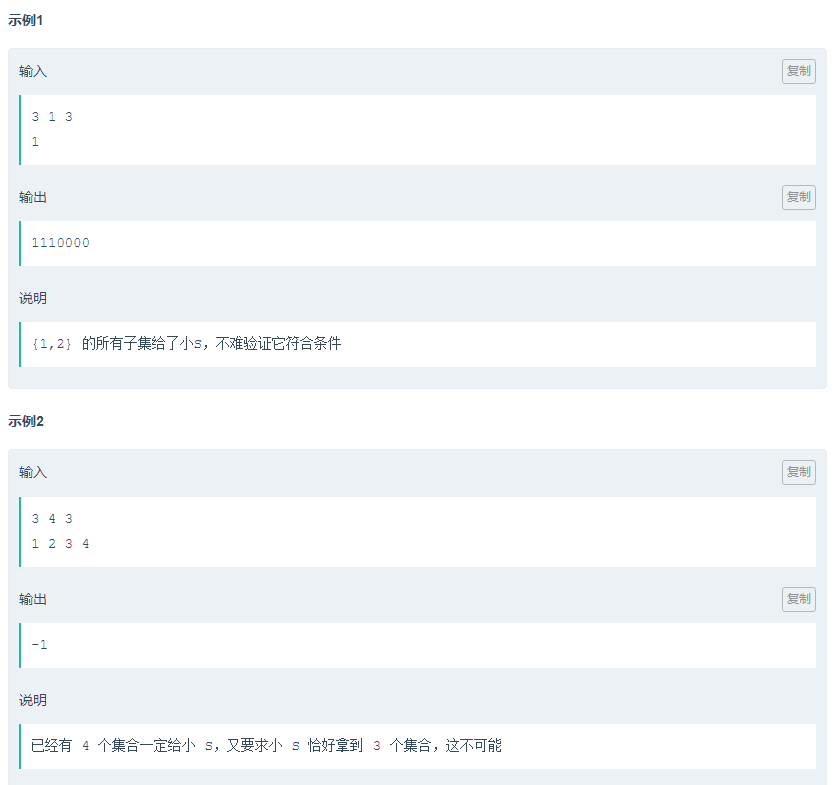
• 考虑m为零的情况，其实只要定义一种分配方案使得每种 k 都能被满足。那么，就是二进制。
• 为每一个元素确定一个优先级，同时一个集合特征值定义为其中元素的最大优先级。
• 可以发现特征值相同的元素一起被选择的话，一定是满足题目要求的。而且每种特征值所代表
集合的集合个数都恰好为各不相同的2的整数次幂。也就是说每个二进制数都可以被表示了。
（即 k ）
然后就是确定优先级了：
记𝑓[𝑆]表示集合S 里的元素已经被分配了最高的若干优先级，是否可行
转移时枚举接下来的优先级最高的元素是哪个。* 对于每一个合法状态枚举下元素，表示这个元素的优先级大于当前状态的所有元素，
其实这个被枚举的元素的优先级是被当前的状态决定的。
* 又由于一个优先级唯一确定了一个特征值为它的集合大小，所以在k确定了的情况下，
也就划分了优先级的选择状态。
* 那么在转移的时候维护状态满足m个必选的集合。具体而言，假设当前状态为x，被
枚举的元素为y，x 与 y 的异或值为 z，那么必定满足：若当前的优先级未被选择，
则m个元素中不能存在一个集合u使得u|y=u并且u|z=z。
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,p,x,t,tmp; 4 int rank[20],g[300050]; 5 bool vis[300050][20]; 6 int f[300050]; 7 int main() 8 { 9 scanf("%d%d%d",&n,&m,&p); 10 t=(1<<n)-1; 11 for(int i=1;i<=m;++i) 12 { 13 scanf("%d",&x); 14 for(int j=0;j<n;++j) 15 if(x&(1<<j)) 16 vis[x][j]=true; 17 } 18 for(int i=0;i<n;++i) 19 for(int j=0;j<=t;++j) 20 if(vis[j][i]) 21 { 22 for(int k=0;k<n;++k) 23 if(!(j&(1<<k))) 24 vis[j|(1<<k)][i]=true; 25 } 26 memset(f,-1,sizeof(f)); 27 f[0]=0; 28 for(int i=0;i<t;++i) 29 { 30 g[i]=g[i>>1]+(i&1); 31 if(f[i]!=-1) 32 { 33 for(int j=0;j<n;++j) 34 if(!(i&(1<<j))) 35 { 36 if(!(p&(1<<g[i]))&&vis[i|(1<<j)][j]) 37 continue; 38 else 39 f[i|(1<<j)]=j; 40 } 41 } 42 } 43 if(f[t]==-1) 44 printf("-1"); 45 else 46 { 47 tmp=n-1; 48 while(t) 49 { 50 rank[f[t]]=tmp--; 51 t^=(1<<f[t]); 52 } 53 t=(1<<n)-1; 54 for(int i=1;i<=t;++i) 55 { 56 tmp=0; 57 for(int j=0;j<n;++j) 58 if(i&(1<<j)) 59 tmp=max(tmp,rank[j]); 60 printf("%d",(p&(1<<tmp))>0); 61 } 62 } 63 return 0; 64 }
