「美团 CodeM 初赛 Round B」送外卖2---------------状压dp
题目描述
一张 n 个点 m 条有向边的图上,有 q 个配送需求,需求的描述形式为 (si,ti,li,ri)( s_i , t_i , l_i , r_i )(si,ti,li,ri),即需要从点 si 送到 ti, 在时刻 li 之后(包括 lil_ili )可以在 sis_isi 领取货物,需要在时刻 ri 之前(包括 ri)送达 ti ,每个任务只需完成一次。
图上的每一条边均有边权,权值代表通过这条边消耗的时间。在时刻 000 有一个工作人员在点 1 上,求他最多能完成多少个配送任务。
在整个过程中,可以认为领货跟交货都是不消耗时间的,时间只花费在路程上。当然在一个点逗留也是允许的。
输出格式
一个整数,表示最多能完成的任务数量。
样例输入
5 4 3 1 2 1 2 3 1 3 4 1 4 5 1 1 2 3 4 2 3 1 2 3 4 3 4
样例输出
2
样例解释
工作人员可以在时刻 1 到达点 2 ,领取第二个货物后在时刻 2 到达点 3 后交货,逗留到时刻 4 ,领取第三个货物,在时刻 4 到达点 4 并交货。
• 首先的首先,需要明确配送的方式。在配送的途中手中不一定只有一份外卖!
然后出于对数据的敏感,易想到用进制数表示状态。
• 由于每一份外卖有按照程序有三种状态,所以用三进制表示外卖的整体状态,
在dp数组中作为一个维度,剩下时间和当前位置。
• 由于时间是数据中最大的存在,成为了dp的对象,当前位置成为了另一个状
态维度。
• 转移的话,只是合法性的判断了。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,q,x,y,z; 4 int dis[25][25]; 5 int f[60050][25],w,now,ans; 6 int base[15],s[15],t[15],l[15],r[15]; 7 int main() 8 { 9 base[0]=1; 10 for(int i=1;i<=11;++i) 11 base[i]=base[i-1]*3; 12 memset(dis,0x3f,sizeof(dis)); 13 memset(f,0x3f,sizeof(f));f[0][1]=0; 14 scanf("%d%d%d",&n,&m,&q); 15 for(int i=1;i<=m;++i) 16 { 17 scanf("%d%d%d",&x,&y,&z); 18 dis[x][y]=min(dis[x][y],z); 19 } 20 for(int i=1;i<=n;++i) 21 dis[i][i]=0; 22 for(int k=1;k<=n;++k) 23 for(int i=1;i<=n;++i) 24 for(int j=1;j<=n;++j) 25 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]); 26 for(int i=0;i<q;++i) 27 scanf("%d%d%d%d",&s[i],&t[i],&l[i],&r[i]); 28 m=base[q]-1; 29 for(int i=0;i<=m;++i) 30 { 31 for(int j=1;j<=n;++j) 32 { 33 for(int k=0;k<q;++k) 34 { 35 now=i/base[k]%3; 36 if(now==0) 37 f[i+base[k]][s[k]]=min(f[i+base[k]][s[k]],max(f[i][j]+dis[j][s[k]],l[k])); 38 else if(now==1&&f[i][j]+dis[j][t[k]]<=r[k]) 39 f[i+base[k]][t[k]]=min(f[i+base[k]][t[k]],f[i][j]+dis[j][t[k]]); 40 41 } 42 if(f[i][j]<f[0][0]) 43 { 44 w=0; 45 for(int k=0;k<=10;++k) 46 if(i/base[k]%3==2) 47 ++w; 48 ans=max(ans,w); 49 } 50 } 51 } 52 printf("%d",ans); 53 return 0; 54 }

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,q,x,y,z; 4 int dis[25][25]; 5 int f[60050][25],w,now,ans; 6 int base[15],s[15],t[15],l[15],r[15]; 7 int main() 8 { 9 base[0]=1; 10 for(int i=1;i<=11;++i) 11 base[i]=base[i-1]*3; 12 memset(dis,0x3f,sizeof(dis)); 13 memset(f,0x3f,sizeof(f));f[0][1]=0; 14 scanf("%d%d%d",&n,&m,&q); 15 for(int i=1;i<=m;++i) 16 { 17 scanf("%d%d%d",&x,&y,&z); 18 dis[x][y]=min(dis[x][y],z); 19 } 20 for(int i=1;i<=n;++i) 21 dis[i][i]=0; 22 for(int k=1;k<=n;++k) 23 for(int i=1;i<=n;++i) 24 for(int j=1;j<=n;++j) 25 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]); 26 for(int i=0;i<q;++i) 27 scanf("%d%d%d%d",&s[i],&t[i],&l[i],&r[i]); 28 m=base[q]-1; 29 for(int i=0;i<=m;++i) 30 { 31 for(int j=1;j<=n;++j) 32 { 33 if(f[i][j]==f[0][0]) 34 continue; 35 for(int k=0;k<q;++k) 36 { 37 now=i/base[k]%3; 38 if(now==0) 39 f[i+base[k]][s[k]]=min(f[i+base[k]][s[k]],max(f[i][j]+dis[j][s[k]],l[k])); 40 else if(now==1&&f[i][j]+dis[j][t[k]]<=r[k]) 41 f[i+base[k]][t[k]]=min(f[i+base[k]][t[k]],f[i][j]+dis[j][t[k]]); 42 43 } 44 w=0; 45 for(int k=0;k<=10;++k) 46 if(i/base[k]%3==2) 47 ++w; 48 ans=max(ans,w); 49 } 50 } 51 printf("%d",ans); 52 return 0; 53 }
这两份代码在思路上是完全一致的。但是……

相似的结果还发生在另一个状压题上(第二份代码直接是TLE 了):
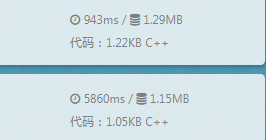
这究竟是种怎样的操作?

如果当前状态完全不可能被转移到的话,就完全没必要对它进行暴力扩展了,果断continue。


