各种运算模型
模型的假设检验(F与T)
F检验:提出原假设和备择假设 之后计算统计量与理论值 最后比较
(F检验主要检验的是模型是否合理)
# 导⼊第三⽅模块 import numpy as np # 计算建模数据中因变量的均值 ybar=train.Profit.mean() # 统计变量个数和观测个数 p=model2.df_model n=train.shape[0] # 计算回归离差平⽅和 RSS=np.sum((model2.fittedvalues-ybar)**2) # 计算误差平⽅和 ESS=np.sum(model2.resid**2) # 计算F统计量的值 F=(RSS/p)/(ESS/(n-p-1)) print('F统计量的值:',F) F统计量的值:174.6372 # 导⼊模块 from scipy.stats import f # 计算F分布的理论值 F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1) print('F分布的理论值为:',F_Theroy) out: F分布的理论值为: 2.5026
计算出来的F统计量值174.64远远⼤于F分布的理论值2.50
所以应当拒绝原假设(先假设模型不合理)
T检验更加侧重于检验模型的各个参数是否合理
model.summary() # 绝对值越小影响越大
1.自变量的个数大于样本量
表头数据列数大于数据条数,算式会无法计算

2.自变量之间存在多重共线性
数据列数之间存在特殊联系,算式会无法计算

岭回归模型
在线性回归模型的基础之上添加一个l2惩罚项(平方项、正则项)
(该模型最终转变成求解圆柱体与椭圆抛物线的焦点问题)

Lasso回归模型
在线性回归模型的基础之上添加一个l1惩罚项(绝对值项、正则项)
相较于岭回归降低了模型的复杂度
(该模型最终转变成求解正方体与椭圆抛物线的焦点问题)

交叉验证
将所有数据都参与到模型的构建和测试中 最后生成多个模型
(从所有数据中随机移除一小部分后制作模型,重复多次,生产多个模型)
再从多个模型中筛选出得分最高(准确度)的模型

将线性回归模型的公式做Logit变换即为Logistic回归模型
将预测问题变成了0到1之间的概率问题

准确率:表示正确预测的正负例样本数与所有样本数量的⽐值,即(A+D)/(A+B+C+D)。
正例覆盖率:表示正确预测的正例数在实际正例数中的⽐例,即D/(B+D)。
负例覆盖率:表示正确预测的负例数在实际负例数中的⽐例,即A/(A+C)。
正例命中率:表示正确预测的正例数在预测正例数中的⽐例,即D/(C+D),

1.ROC曲线
通过计算AUC阴影部分的面积来判断模型是否合理(通常大于0.8表示OK)

2.KS曲线
通过计算两条折现之间最大距离来衡量模型是否合理(通常大于0.4表示OK)

默认情况下解决分类问题(买与不买、带与不带、走与不走)
也可以切换算法解决预测问题(具体数值多少)
(树其实是一种计算机底层的数据结构,与现实不同
计算机里面的树都是自上而下的生长)
决策树则是算法模型中的一种概念,有三个主要部分
根节点、枝节点、叶子节点
(根节点与枝节点用于存放条件,叶子节点存放真正的数据结果)

1.信息熵
eg:信息熵小相当于红绿灯情况,信息熵大相当于买彩票中奖情况

2.条件熵
条件熵其实就是由信息熵再次细分而来
比如有九个用户购买了商品五个没有购买 那么条件熵就是继续从购买不购买的用户中再选择一个条件
(比如按照性别计算男和女的熵)

3.信息增益
信息增益可以反映出某个条件是否对最终的分类有决定性的影响
在构建决策树时根节点与枝节点所放的条件按照信息增益由大到小排

4.信息增益率
决策树中的ID3算法使⽤信息增益指标实现根节点或中间节点的字段选择,但是该指标存在⼀个⾮常明显的缺点,即信息增益会偏向于取值较多的字段。
为了克服信息增益指标的缺点,提出了信息增益率的概念,它的思想很简单,就是在信息增益的基础上进⾏相应的惩罚。

基尼指数
可以让模型解决预测问题

基尼指数增益
与信息增益类似,还需要考虑⾃变量对因变量的影响程度,即因变量的基尼指数下降速度的快慢,下降得越快,⾃变量对因变量的影响就越强

随机森林中每颗决策树都不限制节点字段选择,有多棵树组成的随机森林
在解决分类问题的时候采用投票法、解决预测问题的时候采用均值法

思想:根据位置样本点周边K个邻居样本完成预测或者分类

K值的选择
1.先猜测
2.交叉验证
3.作图选择最合理的k值
准确率(越大越好) MSE(越小越好)


过拟合与欠拟合
过拟合:过于精确,导致容易被误导
欠拟合:太模糊,导致得到的结果准确性太差

距离
欧式距离
两点之间的直线距离

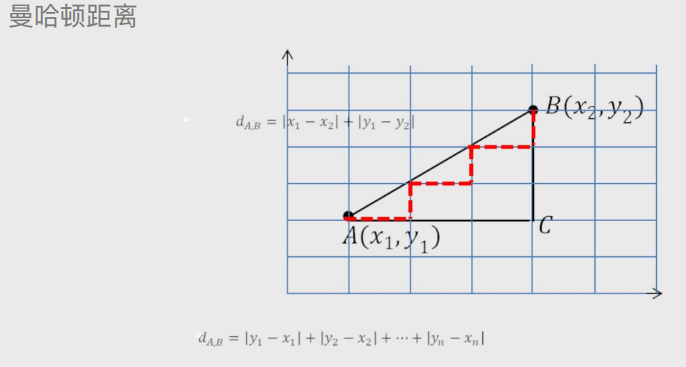
曼哈顿距离
默认两点直接有障碍物
余弦相似度
论文查重





