洛谷p3605(树状数组)
[USACO17JAN]Promotion Counting P
题目描述
奶牛们又一次试图创建一家创业公司,还是没有从过去的经验中吸取教训--牛是可怕的管理者!
为了方便,把奶牛从 1~ n 编号,把公司组织成一棵树,1 号奶牛作为总裁(这棵树的根节点)。除了总裁以外的每头奶牛都有一个单独的上司(它在树上的 “双亲结点”)。
所有的第 i 头牛都有一个不同的能力指数 pi,描述了她对其工作的擅长程度。如果奶牛 i 是奶牛 j 的祖先节点,那么我们我们把奶牛 j 叫做 i 的下属。
不幸地是,奶牛们发现经常发生一个上司比她的一些下属能力低的情况,在这种情况下,上司应当考虑晋升她的一些下属。你的任务是帮助奶牛弄清楚这是什么时候发生的。简而言之,对于公司的中的每一头奶牛 i,请计算其下属 j 的数量满足 pj > pi。
输入格式
输入的第一行包括一个整数 n。
接下来的 n 行包括奶牛们的能力指数 p1,p2 ~ pn。保证所有数互不相同。
接下来的 n-1 行描述了奶牛 2 ~ n 的上司的编号。再次提醒,1 号奶牛作为总裁,没有上司。
输出格式
输出包括 n 行。输出的第 i 行应当给出有多少奶牛 i 的下属比奶牛 i 能力高。
样例 #1
样例输入 #1
5
804289384
846930887
681692778
714636916
957747794
1
1
2
3
样例输出 #1
2
0
1
0
0
提示
【数据范围】
对于 100% 的数据,1<= n <= 105,$1 <= pi<= 109。
技巧:树状数组+离散化+树映射到一个区间
重点介绍如何将树映射到一个空间
我们来一个样例来说明 (其实就是题目的样例)
3
4
1
2
5
1
1
2
3
它生成的树长这个样

我们来看将他们映射到区间后的图
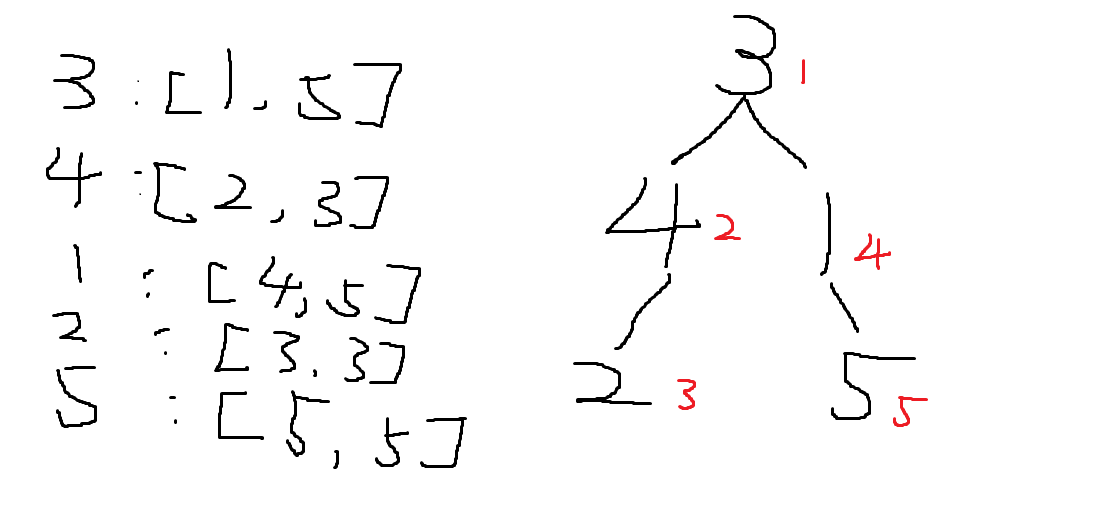
那么是如何做到的呢?
这就需要两个数组+一次dfs就能办到
两个数组分别是:st [N] 和 ed[N] ,st[i] 表示子树i对应区间的头,ed[i] 表示子树i对应区间的尾
例: st[3] = 1, ed[3] = 5;
st[4] = 2, ed[4] = 3;
之后就需要树状数组求逆序对的知识
让我们来模拟一下如何就得答案这个过程
for循环从大到小遍历
(1)5, ans[5] = sum(ed[5]) - sum(st[5]) = 0, (ed[5]= 5, st[5] = 5, 等价于 sum(5) - sum(5) = 0)树状数组更新tree[5] = 1;
(2)4, ans[4] = sum(ed[4]) - sum(st[4]) = 0, (ed[4] = 3, st[4] = 2, 等价于 sum(3) - sum(2) = 0)树状数组更新tree[2] = 1;
(3)3, ans[3] = sum(ed[3]) - sum(st[3]) = 2, (ed[3] = 5, st[3] = 1, 等价于 sum(5) - sum(1) = 2) 数组数组更新tree[1] = 1;
(4) 2, ans[2] = sum(ed[2]) - sum(st[2]) = 0, (ed[2] = 3, st[2] = 3, 等价于 sum(3) - sum(3) = 0) 树状数组更新tree[3] = 1;
(5)1 , ans[1] = sum(ed[1]]) - sum(st[1]) = 1, (ed[1] = 5, st[1] = 4 , 等价于 sum(5) - sum(4) = 1) 树状数组更新为tree[4] = 1;
#define _CRT_SECURE_NO_WARNINGS 1
#include<algorithm>
#include<fstream>
#include<iostream>
#include<cstdio>
#include<deque>
#include<string>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<unordered_map>
using namespace std;
#define INF 0x3f3f3f3f
#define MAXN 310000
#define N 100210
#define M (int)1e8-3
#define endl '\n'
#define exp 1e-8
#define lc p << 1
#define rc p << 1|1
#define lowbit(x) ((x)&-(x))
const double pi = acos(-1.0);
typedef long long LL;
typedef unsigned long long ULL;
inline ULL read() {
ULL x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch>'9') {
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
void print(ULL x) {
if (x > 9)print(x / 10);
putchar(x % 10 ^ 48);
}
int tree[N], n, m,tot,st[N],ed[N],run[N],ans[N]; // tree[]树状数组,st[],ed[],tot,用来将子树映射到区间上。
vector<int>e[N]; //邻接表存边,不谈 //run[]存储离散化后的数组 ,ans[]存储答案
struct node
{
int v,i;
bool operator < (const node& a)const
{
return v < a.v;
}
}arr[N]; //用来离散化的
void update(int x, int d)
{
while (x <= N)
{
tree[x] += d;
x += lowbit(x);
}
}
int sum(int x)
{
int res = 0;
while (x)
{
res += tree[x];
x -= lowbit(x);
}
return res;
}
void dfs(int x)
{
if (x == 0)return; //通过st[],ed[] + dfs 将子树x映射到一个区间st[x]~ed[x]中,看不懂的可以自己模拟一下
tot++;
st[x] = tot;
for (auto ed : e[x])
{
dfs(ed);
}
ed[x] = tot;
return;
}
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> arr[i].v;
arr[i].i = i;
}
sort(arr + 1, arr + 1 + n);
for (int i = 1; i <= n; i++)
{
run[arr[i].i] = i;
}
//上面是离散化
for (int i = 2; i <= n; i++)
{
int a;
cin >> a;
e[run[a]].push_back(run[i]);
}
dfs(run[1]); //将树映射到区间
for (int i = n; i >= 1; i--) //反着写,是为了求得有几个数比我大
{
ans[i] = sum(ed[i]) - sum(st[i]); //求得答案
update(st[i], 1);
}
for (int i = 1; i <= n; i++) //这样写是为了保证输出顺序正确
{
cout << ans[run[i]] << endl;
}
return 0;
}



