PTA 红豆生南国
题目:
有诗云:
相思 (王维 唐)红豆生南国, 春来发几枝。
愿君多采撷, 此物最相思。
那么,我们来采红豆吧!
假设红豆树是这个样子的:
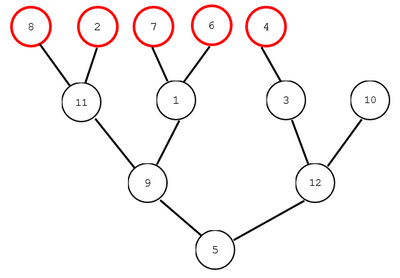
这种红豆树的特点是:
- 每个结点都有一个正整数编号,标在结点内部。结点的编号各不相同。
- 最上方一层结点是 “
红豆”(图中红圈所示的5个结点),这一层被称之为红豆层。 - 树的根结点、左子结点、右子结点、左子树、右子树等的定义与“数据结构”中的“二叉树”相同,但它毕竟是“自然界中的树”,树根在最下方,如图中的
结点5 - 图中这棵红豆树是“完全二叉红豆树”,类似“数据结构”中的“完全二叉树”。(“完全二叉树”的定义:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是完美二叉树。对于一个有N个结点的二叉树,若其结点对应于相同深度完美二叉树的层序遍历的前 N 个结点,这样的树就是完全二叉树) 从图上看,就是:要么每一层(包括红豆层)的结点数达到最大值,要么只在红豆层的最右边缺少一些结点。
对于红豆树,我们定义两种遍历顺序:
正序遍历:先访问树根结点,再正序遍历其左子树,最后正序遍历其右子树逆序遍历:先逆序遍历其右子树,再逆序遍历其左子树,最后访问树根结点
对于给定的一棵完全二叉红豆树以及一些要采撷的结点,计算每次采撷能采到的红豆数量。
注意:我们采的点,可能是红豆,也可能不是红豆。采撷一个结点的意思是,把这个结点及这个结点的子树的全部结点从树中采下来。
例如:若采结点7,这是红豆结点,我们将获得1颗红豆;若采结点11,这不是红豆结点(而是一个枝结点!),我们将获得红豆树的一枝,包含2个红豆结点(8和2)。
输入格式:
输入有四行。
第一行是一个不超过60的正整数N,表示完全二叉红豆树中的结点数量。
第二行是N个不超过1000的结点编号序列,以空格间隔,表示的是这棵树的逆序遍历序列。
第三行是一个不超过N的正整数K,表示进行K次采撷。
第四行是K个正整数,依次表示每次要采的结点编号。
输出格式:
输出包含K+1行,
前K行,对于输入的每个采撷的点,在一行输出相应获得的红豆数量。如果这个点已经被采掉了,则输出Zao Jiu Cai Diao Le!。如果这个点在原树中根本不存在,则输出Kan Qing Chu Le?。
最后一行,输出采撷结束之后,这棵红豆树的正序遍历序列,用空格分隔,最后一个结点之后没有空格。如果采撷结束之后树已空,则输出Kong Le!
输入样例1:
对于题目中给出的图,对应的输入是:
12
10 4 3 12 6 7 1 2 8 11 9 5
4
15 12 11 2
输出样例1:
Kan Qing Chu Le?
1
2
Zao Jiu Cai Diao Le!
5 9 1 7 6
输入样例2:
对于题目中给出的图,对应的输入是:
12
10 4 3 12 6 7 1 2 8 11 9 5
1
5
输出样例2:
5
Kong Le!一道很有意思的二叉树的题
分析:难点在于建树,因为他只给了逆序遍历,通常确定一棵二叉树需要正序遍历或逆序遍历加上中序遍历才能确认,但因为这道题明确表示是一棵完全二叉树,所以可以不加上中序遍历就能确认。
详情见代码
点击查看代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<algorithm>
#include<fstream>
#include<iostream>
#include<cstdio>
#include<deque>
#include<string>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<unordered_map>
using namespace std;
#define INF 0x3f3f3f3f
#define MAXN 310000
#define N 200010
#define endl '\n'
#define exp 1e-8
#define lc p << 1
#define rc p << 1|1
#define lowbit(x) ((x)&-(x))
const double pi = acos(-1.0);
typedef long long LL;
typedef unsigned long long ULL;
inline ULL read() {
ULL x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch>'9') {
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
void print(ULL x) {
if (x > 9)print(x / 10);
putchar(x % 10 ^ 48);
}
int t[N];
int b[10] = { 0,1,3,7,15,31,63},n,h,ha[N],f[N];
void build(int p) //建树
{ //因为是一棵完全二叉树,所以可以由正序遍历或逆序遍历确认
if (p <= n)
{
build(2 * p + 1); //逆序遍历这样建树,正序的话就要反过来(为什么能这样建树,可以自己模拟一遍)
build(2 * p);
cin >> t[p];
ha[t[p]] = p; //将输入的数字与结点的数值对应上,方便之后查找结点在不在树上
}
}
int pick(int p) //摘果子
{
if (t[p]== 0)return 0; //如果等于0,说明这个结点被采过了,直接returnn 0;
if (f[p]&&t[p]) { t[p]= 0; return 1; } //如果是果子则将其置为0表示摘过了,再返回1
t[p] = 0; //遍历到一个结点,就将该节点置为0,表示摘过了
return pick(2 * p) + pick(2 * p + 1); //返回自己这棵树有几个果子
}
void Print(int p) //打印函数
{
if (t[p])
{
printf(" %d", t[p]);
Print(2 * p);
Print(2 * p + 1);
}
}
int main()
{
cin >> n;
build(1);
int x = 0;
while (b[x] < n) //完全二叉树的倒数的二层到第一层一定是满二叉树,所以最后一层为b[i]+1到n (b[i]表示这棵树中最大的满二叉树的结点个数)
x++; //当b[x]大于等于n时,跳出循环,此时b[x-1]就是棵树中最大的满二叉树的结点个数
for (int i = b[x - 1] + 1; i <= n; i++) //求得该二叉树的最后一层的结点
f[i] = 1; //标记最后一层结点为果子
int k = 0;
cin >> k;
while (k--)
{
int a;
cin >> a;
int p = ha[a];
if (!p)
puts("Kan Qing Chu Le?");
else
{
if (t[p])
{
cout << pick(p) << endl;
}
else
{
puts("Zao Jiu Cai Diao Le!");
}
}
}
if (t[1])
{
printf("%d", t[1]);
Print(2);
Print(3);
cout << endl;
}
else
puts("Kong Le!");
return 0;
}





