换根树链剖分

关于这篇文章

刚写完 《树链剖分》 不到两天，刷了各个网站的树链剖分模板题

然后碰到了 LOJ的树链剖分模板，然后就直接交了 Luogu模板的代码

然后就 RE 了

仔细再一看，(⊙o⊙)？咋就还要换根？完全不按套路出牌？？？

于是学习了树链剖分维护换根操作，写下此文以记录学习成果

注意：这篇文章是基于基础树链剖分的扩展，如果不会树链剖分请出门左转，《树链剖分》

例题

原题是在LOJ上，传送门

我在洛谷上做了一个 镜像题

题意如下：

给定一棵 \(n\) 个节点的树，初始时该树的根为 \(1\) 号节点，每个节点有一个给定的权值。下面依次进行

个操作，操作分为如下五种类型：

• 换根：将一个指定的节点设置为树的新根。
• 修改路径权值：给定两个节点，将这两个节点间路径上的所有节点权值（含这两个节点）增加一个给定的值。
• 修改子树权值：给定一个节点，将以该节点为根的子树内的所有节点权值增加一个给定的值。
• 询问路径：询问某条路径上节点的权值和。
• 询问子树：询问某个子树内节点的权值和。

（题意完全copy自原题）

分析

首先，忽视第一种操作，后四种操作都是标准的重链剖分

所以这篇文章重点讲述如何维护换根

分类讨论

俗话说的好，整体不会就分类

我们考虑一下换根对于其余四种操作的影响

换根对于路径应该是没有影响的，原因是因为不论根如何，树上两点之间有且仅有一条唯一的路径

（注意：此处的路径指的是不走重复点的路径，或者也可以理解为最短路径）

所以换根只对子树会有影响，那具体来说，会有什么影响呢？

假设原来根为 \(1\)，要查询的子树为 \(u\)，子树 \(u\) 在根为 \(1\) 时为子树 \(u'\)，换过的根为 \(r\)

那么如果 \(u\) 在根为 \(1\) 时不为 \(r\) 的祖先（在这里定义的一个节点的祖先包含其本身），子树 \(u\) 与子树 \(u'\) 相同

这种情况下，就直接输出维护的值就好了

否则呢？

如果 \(u=r\)，直接输出总体值就好了

但如果 \(u \neq r\) 呢？就可以找一下规律，如下图所示：

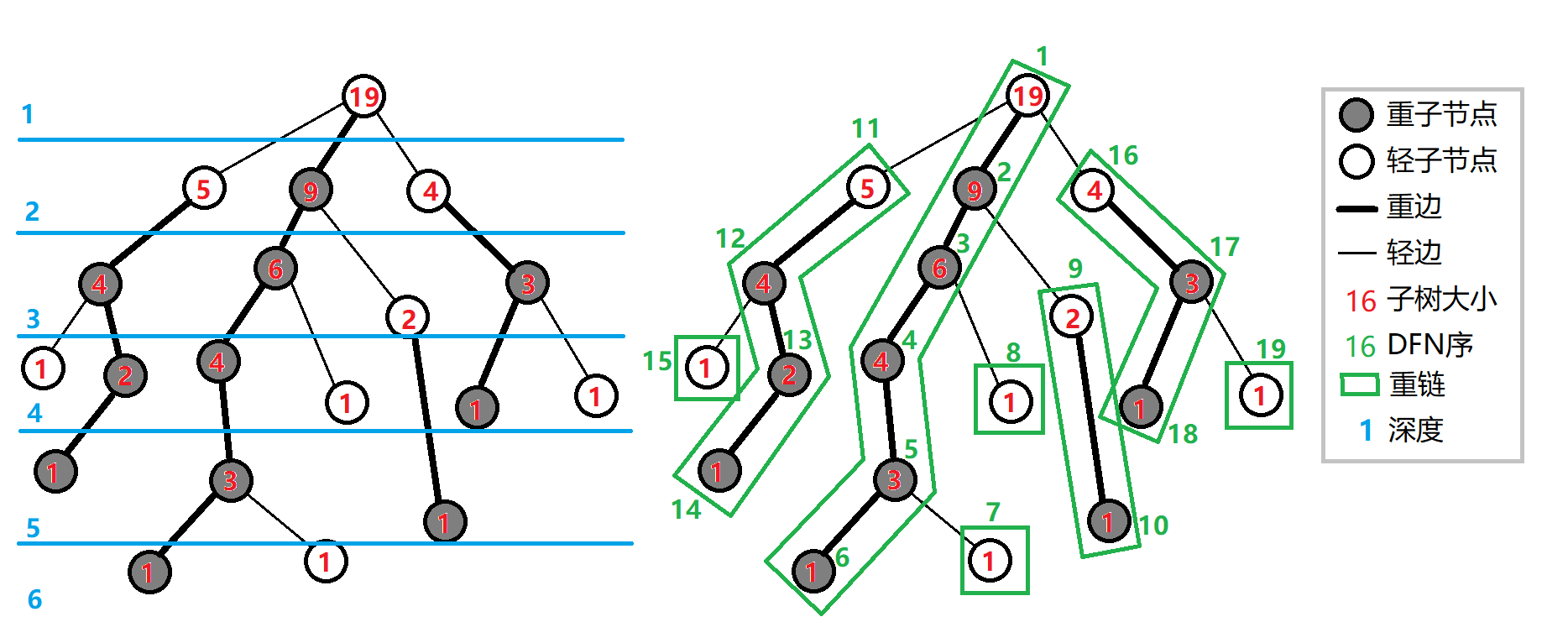
在图中随便找一组 \(u,r\) 试验一下，发现如下规律：

对于 \(u,r\)，找到 \(u\) 的儿子 \(v\)，并且满足 \(v\) 是 \(r\) 的祖先

这时，\(u\) 的子树和减去 \(v\) 的子树和就是 \(u'\) 的子树和

然后问题就彻底解决了

但对于修改呢？很简单，比如要将子树 \(u'\) 加上 \(k\)

那就先将子树 \(u\) 加上 \(k\)，然后再将子树 \(v\) 加上 \(-k\)

模板题代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define int long long
const int MAXN=1e5+7;
struct Edge
{
    int v,nxt;
} e[MAXN<<1];
int d[MAXN<<2],b[MAXN<<2],dfn[MAXN],cnt,head[MAXN],tot,a[MAXN];
int dep[MAXN],bd[MAXN],hs[MAXN],sz[MAXN],tp[MAXN],val[MAXN],fa[MAXN],n,m,r;

inline void add(int u,int v)
{
    e[++tot].v=v;
    e[tot].nxt=head[u];
    head[u]=tot;
}

void dfs1(int u,int f)
{
    fa[u]=f;
    dep[u]=dep[f]+1;
    sz[u]=1;
    for(int i=head[u]; i; i=e[i].nxt)
    {
        int v=e[i].v;
        if(v==f) continue;
        dfs1(v,u);
        sz[u]+=sz[v];
        if(sz[v]>sz[hs[u]]) hs[u]=v;
    }
}

void dfs2(int u,int tpf)
{
    tp[u]=tpf;
    dfn[u]=++cnt;
    bd[cnt]=u;
    val[cnt]=a[u];
    if(!hs[u]) return;
    dfs2(hs[u],tpf);
    for(int i=head[u]; i; i=e[i].nxt)
    {
        int v=e[i].v;
        if(v==fa[u]||v==hs[u])continue;
        dfs2(v,v);
    }
}
inline void pushup(int p)
{
    d[p]=d[p<<1]+d[(p<<1)+1];
}

inline void pushdown(int p,int l,int r)
{
    if(!b[p])return;
    int mid=(l+r)>>1;
    b[p<<1]+=b[p];
    b[(p<<1)+1]+=b[p];
    d[p<<1]+=(mid-l+1)*b[p];
    d[(p<<1)+1]+=(r-mid)*b[p];
    b[p]=0;
}

void build(int p,int l,int r)
{
    if(l==r)
    {
        d[p]=val[l];
        return;
    }
    int mid=(l+r)>>1;
    build(p<<1,l,mid),build((p<<1)+1,mid+1,r);
    pushup(p);
}
void update(int p,int l,int r,int u,int v,int a)
{
    if(u<=l&&r<=v)
    {
        d[p]+=(r-l+1)*a;
        b[p]+=a;
        return;
    }
    pushdown(p,l,r);
    int mid=(l+r)>>1;
    if(u<=mid) update(p<<1,l,mid,u,v,a);
    if(mid<v) update((p<<1)+1,mid+1,r,u,v,a);
    pushup(p);
}
int query(int p,int l,int r,int u,int v)
{
    if(u<=l&&r<=v)return d[p];
    pushdown(p,l,r);
    int mid=(l+r)>>1,ans=0;
    if(u<=mid) ans+=query(p<<1,l,mid,u,v);
    if(mid<v) ans+=query((p<<1)+1,mid+1,r,u,v);
    return ans;
}
void padd(int u,int v,int a)
{
    while(tp[u]!=tp[v])
    {
        if(dep[tp[u]]<dep[tp[v]]) swap(u,v);
        update(1,1,n,dfn[tp[u]],dfn[u],a);
        u=fa[tp[u]];
    }
    if(dep[u]>dep[v]) swap(u,v);
    update(1,1,n,dfn[u],dfn[v],a);
}
int pquery(int u,int v)
{
    int ans=0;
    while(tp[u]!=tp[v])
    {
        if(dep[tp[u]]<dep[tp[v]]) swap(u,v);
        ans+=query(1,1,n,dfn[tp[u]],dfn[u]);
        u=fa[tp[u]];
    }
    if(dep[u]>dep[v]) swap(u,v);
    ans+=query(1,1,n,dfn[u],dfn[v]);
    return ans;
}

inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*f;
}

int lca(int x,int y)
{
    while(tp[x]!=tp[y])
    {
        if(dep[tp[x]]>dep[tp[y]]) x=fa[tp[x]];
        else y=fa[tp[y]];
    }
    return dep[x]<dep[y]?x:y;
}

int check(int u)
{
    if(u==r) return -1;
    if(dfn[u]<=dfn[r]&&dfn[r]<=dfn[u]+sz[u]-1)
    {
        int v=r;
        while(dep[v]>dep[u])
        {
            if(fa[tp[v]]==u) return tp[v];
            v=fa[tp[v]];
        }
        return hs[u];
    }
    return 0;
}

signed main()
{
    n=read();
    r=1;
    for(int i=1; i<=n; i++) a[i]=read();
    for(int i=2; i<=n; i++)
    {
        int f=read();
        add(f,i),add(i,f);
    }
    dfs1(1,0);
    dfs2(1,1);
    build(1,1,n);
    m=read();
    for(int i=1; i<=m; i++)
    {
        int opt=read();
        if(opt==1) r=read();
        else if(opt==2)
        {
            int u=read(),v=read(),k=read();
            padd(u,v,k);
        }
        else if(opt==3)
        {
            int u=read(),k=read();
            int v=check(u);
            if(v==-1) update(1,1,n,1,n,k);
            else if(v==0) update(1,1,n,dfn[u],dfn[u]+sz[u]-1,k);
            else
            {
                update(1,1,n,1,n,k);
                update(1,1,n,dfn[v],dfn[v]+sz[v]-1,-k);
            }
        }
        else if(opt==4)
        {
            int u=read(),v=read();
            printf("%lld\n",pquery(u,v));
        }
        else
        {
            int u=read(),v=check(u),ans;
            if(v==-1) ans=query(1,1,n,1,n);
            else if(v==0) ans=query(1,1,n,dfn[u],dfn[u]+sz[u]-1);
            else ans=query(1,1,n,1,n)-query(1,1,n,dfn[v],dfn[v]+sz[v]-1);
            printf("%lld\n",ans);
        }
    }
    return 0;
}