CodeForces 50C 题解

题解笔记

CF50C Happy Farm 5(farm.cpp)

时间限制 $2s$ | 内存限制 $256M$

题目描述：

平面直角坐标系上有 $n$ 个整数点（横纵坐标都是整数），请你计算将所有点严格包围的路径最少要移动多少步。路径的每一步只能走整点，且每次只能向上、下、左、右、左上、左下、右上、右下的 $8$ 个方向移动一格。严格包围要求所有的点不能在路径上。

输入格式：

第一行仅有一个正整数 $n$ （$1 \leq n \leq 10^5$），接下来的 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$ （ $ \mid x_i \mid , \mid y_i \mid \leq 10^6$ ），分别表示一个点的横纵坐标，数据保证没有两个点重合。

输出格式：

一个数，表示最短的路径步数。

输入输出样例：

样例1输入	样例1输出
4 1 1 5 1 5 3 1 3	16

样例解释

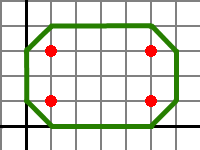
解题思路：

首先要先了解几个概念：

凸多边形

没有任何一个内角是优角的多边形。

凸包

在平面上能包含所有给定点的最小凸多边形叫做凸包。

其定义为：对于给定集合 $X$ ，所有包含 $X$ 的凸集的交集 $S$ 被称为 $X$ 的凸包。

实际上可以理解为用一个橡皮筋包含住所有给定点的形态。

凸包用最小的周长围住了给定的所有点。如果一个凹多边形围住了所有的点，它的周长一定不是最小，如下图。根据三角不等式，凸多边形在周长上一定是最优的。

凸包的一周称为凸壳

严格凸包与非严格凸包

非严格凸包：只要围住了点集 $X$ 中的每一个点的凸包就是非严格凸包

严格凸包：围住了点集 $X$ 中的每一个点且凸壳上不存在点集中的点的凸包

这道题有很多种思路

首先，一看到这道题，一下子就觉得这道题是求严格凸包

那如果用凸包的思路的话就有两种思路：

将每个点都复制成上下左右四分，再加上中间的，就成为一个十字，然后再对复制完的点进行求非严格凸包
求非严格凸包，再将凸壳的长度 $+4$ 就是答案

（如果想要看这些思路的代码，请去看参考代码中其他代码一章）

但这道题也有其他的思路，接下来就重点介绍这种思路：

转化为非严格凸包

首先想考虑把这道题转化为求非严格凸包，可以发现，再求完非严格凸包后再 $+4$ 就是严格凸包的凸壳长了

拿样例为例子：

首先，样例的四个点如下图所绘

先求出非严格凸壳

然后再将 $f,g,h,i$ 四条边都向外平移，并将 $f$ 与 $g$， $g$ 与 $h$， $h$ 与 $i$， $i$ 与 $f$ 之间连上一条斜边

如下图所示：

由于 $f,g,h,i$ 四条边长度并没有变，只是增加了 $j,k,l,m$ 四条边，而 $j,k,l,m$ 四条边，合起来也就多耗了 $4$ 步，这就是开头所说 $+4$ 的来源

证明非严格凸包最优路径的形状一定是斜矩形

其实上文在转化为非严格凸包时有一个限制，那就是凸壳一定是一个四边形

首先，可以证明，所有四边形的凸壳都可以转化为矩形的凸壳

需要证明，梯形（这里包含平行四边形）的凸壳可以被转化斜矩形的凸壳

由于这道题，只记录凸壳的长度，且斜着走一步与直着走一步都是一步，所以对凸壳长度的影响都是一样的

万物皆矩形

可以证明最优的凸壳一定为一个矩形：

证明梯形（包括平行四边形）可以被转化为斜矩形

若存在如下四点：

求出他们的凸包为：

于是，我们继续转化 $g$ 这条边，让凸壳更加接近菱形：

但这时，会发现，有一部分的梯形就这样被转化为了菱形，可是有一部分梯形，就如我举出的这一个梯形，它并没有转化为斜矩形，而是被转化为缺了两个角的矩形。

那这时，就需要继续转化凸壳：

将线段 $EF$ 围绕 $E$ 点顺时针旋转 $ 45^\circ $
将线段 $AC$ 围绕 $C$ 点逆时针旋转 $ 45^\circ $

得到下图：

接下来，再把折线 $ABEF'$ 向上平移 $1$ 格：

但这时，就会发现一个问题，就是在变为斜矩形后，$B$ 点不被凸包包含了，但这时，我们将这个非严格凸包转化为严格凸包：

这样的话，就可以说明，所有梯形都能被转换为斜矩形

那剩下的凸壳就是矩形的凸壳，所以所有的凸壳都可以被转化为矩形和菱形的凸壳

正不压斜

接下来，我们就需要证明最优的凸包的凸壳中一定有斜矩形的凸壳

由于所有凸壳都能被转换为矩形的凸壳，所以我们只需要证明斜矩形的凸包 $\leq$ 正矩形的凸壳

可以根据勾股定理来证明

假设有如下三个点：

这时，如果使用正矩形的话，就可以求出如下非严格凸包（凸包长为 $16$ ）：

但如果用斜矩形的话，可以求出更优的凸包（凸包长为 $14$ ）：

由此可以看出，斜矩形最优

当然，也有别的方法来证明斜矩形最优

求出斜矩形

于是，问题又来了，如何求出能够涵括所有点的斜矩形呢？

首先，由于只能走方格的对角线，所以斜矩形的斜率是固定的。

其次，由于是矩形，所以只需要求出两组对边，即两条垂直的边，就可以确定斜矩形的周长。

接下来，就是讲解如何求这两条边

关于下面的第一、二条边指

第一条边指的是平行于平分一三象限的对角线的边

第二条边指的是平行于平分二四象限的对角线的边

求边两部曲（第一条边）

即下图中的 $i$ 和 $g$

这时我们可以发现，我们可以用一三象限的平分线来为点集进行分层

从代数角度来说，每一个点的 $x+y$ 就是这个点的层

对于两个点 $p_1(x_1,y_1),p_2(x_2,y_2)$ 来说：

如果 $x_1+y_1>x_2+y_2$ ，那么 $p_1$ 比 $p_2$ 更偏右上

如果 $x_1+y_1=x_2+y_2$ ，那么 $p_1$ 和 $p_2$ 偏右上的程度一样

否则 $p_1$ 比 $p_2$ 更偏左下

而第一条边的长度的两倍就是 $max(x+y)-min(x+y)$

求边两部曲（第二条边）

与求第一条边的方法相同：

这时我们可以发现，我们可以用二四象限的平分线来为点集进行分层

从代数角度来说，每一个点的 $x-y$ 就是这个点的层

对于两个点 $p_1(x_1,y_1),p_2(x_2,y_2)$ 来说：

如果 $x_1-y_1>x_2-y_2$ ，那么 $p_1$ 比 $p_2$ 更偏左上

如果 $x_1+y_1=x_2+y_2$ ，那么 $p_1$ 和 $p_2$ 偏左上的程度一样

否则 $p_1$ 比 $p_2$ 更偏右下

而第二条边的长度的两倍就是 $max(x-y)-min(x-y)$

综上所述

$\because $

非严格凸包的长度 $=$ 斜矩形的周长 $=$ $max(x+y)-min(x+y)+max(x-y)-min(x-y)$

严格凸包的长度 $=$ 非严格凸包的长度 $+4$

$\therefore $

答案 $=$ 非严格凸包的长度 $=$ $max(x+y)-min(x+y)+max(x-y)-min(x-y)+4$

参考代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int INF=0x3f3f3f3f;
int n;
int rmax=~INF,rmin=INF,lmax=~INF,lmin=INF;

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        rmax=max(rmax,x+y);
        rmin=min(rmin,x+y);
        lmax=max(lmax,x-y);
        lmin=min(lmin,x-y);
    }
    printf("%d",rmax-rmin+lmax-lmin+4);
    return 0;
}

其他代码

求非严格凸包，再将凸壳的长度 $+4$ 就是答案：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define int long long
const int MAXN=1e5+5;
typedef pair<int,int> Point;
int st[MAXN],top;
Point p[MAXN];
inline double cross_times(const Point &a,const Point &b)
{
    return a.first*b.second-a.second*b.first;
}

inline const Point operator-(const Point &p1, const Point &p2)
{
    return Point(p1.first-p2.first,p1.second-p2.second);
}

inline int distance(const Point &p1,const Point &p2)
{
    return max(abs(p1.first-p2.first),abs(p1.second-p2.second));
}

int n;

signed main()
{
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%lld%lld",&p[i].first,&p[i].second);
    }
    sort(p+1,p+n+1);
    st[++top]=1;
    for(int i=2; i<=n; i++)
    {
        while(top>=2&&cross_times(p[st[top]]-p[st[top-1]],p[i]-p[st[top]])<=0) --top;
        st[++top]=i;
    }
    int tmp=top;
    for(int i=n-1; i>=1; i--)
    {
        while(top>tmp&&cross_times(p[st[top]]-p[st[top-1]],p[i]-p[st[top]])<=0) --top;
        st[++top]=i;
    }
    long long ans=0;
    for(int i=1; i<top; i++)
    {
        ans+=distance(p[st[i]],p[st[i+1]]);
    }
    printf("%lld",ans+distance(p[st[top]],p[st[1]])+4);
    return 0;
}

将每个点都复制成上下左右四分，再加上中间的，就成为一个十字，然后再对复制完的点进行求非严格凸包：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define int long long
const int MAXN=5e5+5;
typedef pair<int,int> Point;
int st[MAXN],top;
Point p[MAXN];
inline double cross_times(const Point &a,const Point &b)
{
    return a.first*b.second-a.second*b.first;
}

inline const Point operator-(const Point &p1, const Point &p2)
{
    return Point(p1.first-p2.first,p1.second-p2.second);
}

inline int distance(const Point &p1,const Point &p2)
{
    return max(abs(p1.first-p2.first),abs(p1.second-p2.second));
}

int n,tot;

inline void make_point(int a,int b)
{
    p[++tot].first=a;
    p[tot].second=b;
}

signed main()
{
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        int x,y;
        scanf("%lld%lld",&x,&y);
        make_point(x,y);
        make_point(x-1,y);
        make_point(x+1,y);
        make_point(x,y-1);
        make_point(x,y+1);
    }
    n*=5;
    sort(p+1,p+n+1);
    st[++top]=1;
    for(int i=2; i<=n; i++)
    {
        while(top>=2&&cross_times(p[st[top]]-p[st[top-1]],p[i]-p[st[top]])<=0) --top;
        st[++top]=i;
    }
    int tmp=top;
    for(int i=n-1; i>=1; i--)
    {
        while(top>tmp&&cross_times(p[st[top]]-p[st[top-1]],p[i]-p[st[top]])<=0) --top;
        st[++top]=i;
    }
    long long ans=0;
    for(int i=1; i<top; i++)
    {
        ans+=distance(p[st[i]],p[st[i+1]]);
    }
    printf("%lld",ans+distance(p[st[top]],p[st[1]]));
    return 0;
}

posted @ 2021-11-26 19:54 yhang323 阅读(40) 评论(0) 编辑收藏举报

刷新页面返回顶部

yhang