回溯法学习笔记

回溯法学习笔记

目录

• 回溯法学习笔记
  • 1，什么是回溯法
  • 2，什么时候使用回溯法
  • 3，回溯法的套路
  • 4，例题

1，什么是回溯法

回溯法其实是一种使用递归的暴力搜索法。

2，什么时候使用回溯法

当求解目的是求出满足条件的所有解，且在常规的for循环暴力搜索法无法完成任务的时候，使用回溯法，如：

1. 组合问题
2. 切割字符串
3. 子集问题
4. 排列问题
5. 棋盘问题(n皇后问题等)

该类问题的解往往可以用树形结构表示，如：

请求出集合为1,2,3,的所有排列

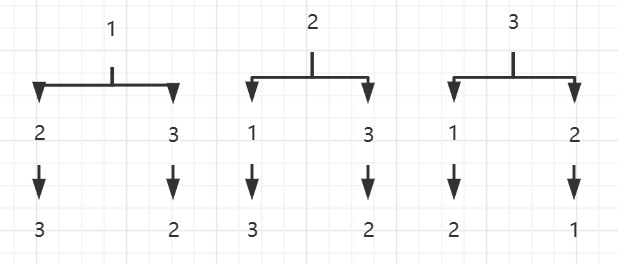
3，回溯法的套路

使用以下模板即可：

void backTracking(参数(一般都有很多参数)){
    if (终止条件){
        收集结果；
        return；
    }
    for (集合元素){
        处理节点；
        递归函数；
        回溯；
    }
}

4，例题

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1：
输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

//按照上述模板即可写出代码
class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList();
        List<Integer> list = new ArrayList();
        List<Integer> temp = new ArrayList(list);
        backTracking(res,list,1,n,k);
        return res;
    }
    public void backTracking(List<List<Integer>> res, List<Integer> list, int start, int n, int k){
        if (k == 0){
            List<Integer> temp = new ArrayList(list);
            res.add(temp);
        }
        for (int i = start; i <= n; i++){
            list.add(i);
            backTracking(res,list,i+1,n,k-1);
            list.remove(list.size()-1);
        }
    }
}