Python实现人工神经网络逼近股票价格
1.基本数据绘制成图
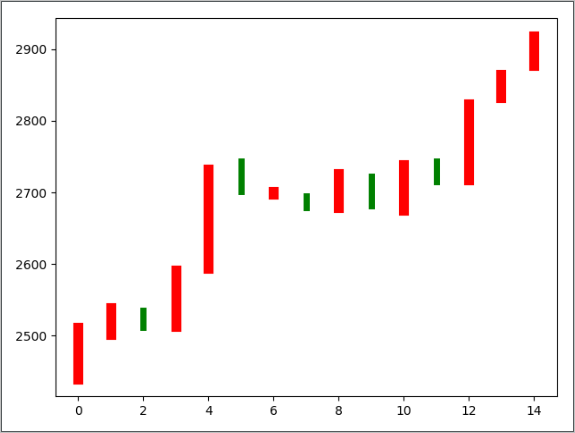
数据有15天股票的开盘价格和收盘价格,可以通过比较当天开盘价格和收盘价格的大小来判断当天股票价格的涨跌情况,红色表示涨,绿色表示跌,测试代码如下:
1 # encoding:utf-8 2 3 import tensorflow as tf 4 import numpy as np 5 import matplotlib.pyplot as plt 6 date = np.linspace(1, 15, 15) 7 # 当天的收盘价格 8 endPrice = np.array([2511.90,2538.26,2510.68,2591.66,2732.98,2701.69,2701.29,2678.67,2726.50,2681.50,2739.17,2715.07,2823.58,2864.90,2919.08] 9 ) 10 # 当天的开盘价格 11 beginPrice = np.array([2438.71,2500.88,2534.95,2512.52,2594.04,2743.26,2697.47,2695.24,2678.23,2722.13,2674.93,2744.13,2717.46,2832.73,2877.40]) 12 print(date) # 打印日期 13 plt.figure() 14 for i in range(0,15): 15 # 通过循环遍历数据画出柱状图 16 dateOne = np.zeros([2]) 17 dateOne[0] = i 18 dateOne[1] = i 19 print(dateOne) 20 priceOne = np.zeros([2]) 21 priceOne[0] = beginPrice[i] 22 priceOne[1] = endPrice[i] 23 if endPrice[i] > beginPrice[i]: 24 # 如果收盘价格大于开盘价格说明股票上涨 用红色表示 lw为线条粗细 25 plt.plot(dateOne, priceOne,'r',lw=8) 26 else: 27 # 如果收盘价格小于开盘价格说明股票下跌 用绿色表示 lw为线条粗细 28 plt.plot(dateOne, priceOne,'g',lw=5) 29 plt.show()
运行后的图如下:
2.人工神经网络进行预测
建立一个简单的三层人工神经网络。
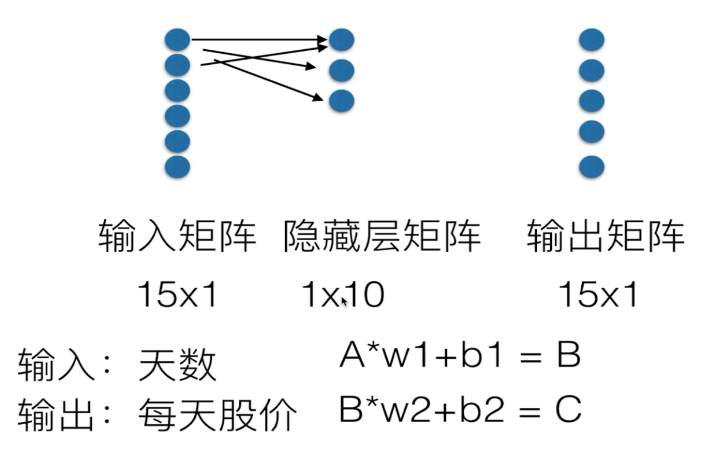

循环的终止条件可以为预先设定的循环次数或者与真实值的差异百分比

功能实现,完整的测试代码如下:
1 # encoding:utf-8 2 3 import tensorflow as tf 4 import numpy as np 5 import matplotlib.pyplot as plt 6 date = np.linspace(1, 15, 15) 7 # 当天的收盘价格 8 endPrice = np.array([2511.90,2538.26,2510.68,2591.66,2732.98,2701.69,2701.29,2678.67,2726.50,2681.50,2739.17,2715.07,2823.58,2864.90,2919.08] 9 ) 10 # 当天的开盘价格 11 beginPrice = np.array([2438.71,2500.88,2534.95,2512.52,2594.04,2743.26,2697.47,2695.24,2678.23,2722.13,2674.93,2744.13,2717.46,2832.73,2877.40]) 12 print(date) # 打印日期 13 plt.figure() 14 for i in range(0,15): 15 # 通过循环遍历数据画出柱状图 16 dateOne = np.zeros([2]) 17 dateOne[0] = i 18 dateOne[1] = i 19 print(dateOne) 20 priceOne = np.zeros([2]) 21 priceOne[0] = beginPrice[i] 22 priceOne[1] = endPrice[i] 23 if endPrice[i] > beginPrice[i]: 24 # 如果收盘价格大于开盘价格说明股票上涨 用红色表示 lw为线条粗细 25 plt.plot(dateOne, priceOne,'r',lw=8) 26 else: 27 # 如果收盘价格小于开盘价格说明股票下跌 用绿色表示 lw为线条粗细 28 plt.plot(dateOne, priceOne,'g',lw=5) 29 # plt.show() 30 # A(15x1)*w1(1x10)+b1(1*10) = B(15x10) 31 # B(15x10)*w2(10x1)+b2(15x1) = C(15x1) 32 # 1 A B C 33 dateNormal = np.zeros([15,1]) 34 priceNormal = np.zeros([15,1]) 35 # 日期和价格进行归一化处理 36 for i in range(0, 15): 37 dateNormal[i, 0] = i/14.0 38 priceNormal[i, 0] = endPrice[i]/3000.0 39 print(dateNormal) 40 print(priceNormal) 41 42 x = tf.placeholder(tf.float32, [None, 1]) # 表明是N行1列的 43 y = tf.placeholder(tf.float32, [None, 1]) # 表明是N行1列的 44 45 # B 46 w1 = tf.Variable(tf.random_uniform([1, 10], 0, 1)) # 可变值 可以通过误差修改值 范围0-1 47 b1 = tf.Variable(tf.zeros([1, 10])) # 可变值 可以通过误差修改值 48 wb1 = tf.matmul(x, w1)+b1 49 layer1 = tf.nn.relu(wb1) # 激励函数 映射成另一个值 50 # 第一二层完毕 51 52 # C 53 w2 = tf.Variable(tf.random_uniform([10, 1], 0, 1)) # 可变值 可以通过误差修改值 范围0-1 54 b2 = tf.Variable(tf.zeros([15, 1])) 55 wb2 = tf.matmul(layer1, w2)+b2 56 layer2 = tf.nn.relu(wb2) # 激励函数 映射成另一个值 57 # 第二三层完毕 58 59 # 误差用loss表示 实际是一个标准差 60 loss = tf.reduce_mean(tf.square(y-layer2)) # y 真实 layer2 计算 61 # 每次调整的步长 梯度下降0.1 目的是缩小loss减小真实值与误差值的差异 62 train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) 63 with tf.Session() as sess: 64 sess.run(tf.global_variables_initializer()) # 初始化 65 for i in range(0, 10000): # 训练次数为10000 66 sess.run(train_step, feed_dict={x: dateNormal, y: priceNormal}) 67 # w1w2 b1b2 A + wb -->layer2 68 pred = sess.run(layer2, feed_dict={x: dateNormal}) 69 predPrice = np.zeros([15, 1]) # 预测结果 70 for i in range(0, 15): # 还原数据需要*3000 71 predPrice[i, 0] = (pred*3000)[i, 0] 72 plt.plot(date, predPrice, 'b', lw=1) 73 plt.show()
运行结果如下:(图中蓝色的线表示股票的预测值)




