2018ACM-ICPC南京区域赛---AJGIDKM
含【最小球覆盖】【最大流isap】模板。
题面pdf
G---Pyramid【数论】【规律】【递推式】
题意:
度为$n$的Pyramid是一个由$\frac{n(n+1)}{2}$个三角形组成大三角形。比如度为3的Pyramid是下面这样子。
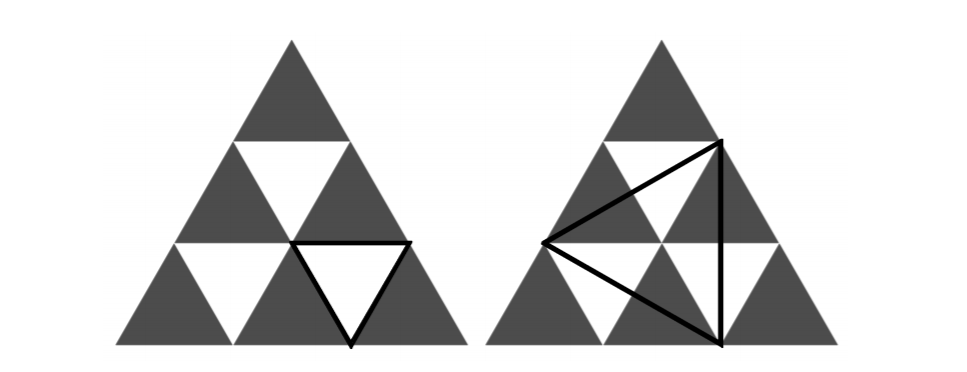
现在由这些顶点组成等边三角形,问有多少个。
思路:
zyn先放到坐标系里打了个表,然后发现差的差是一个等差数列....
于是就可以有递推关系式了。矩阵快速幂T了
所以只能解方程,把系数解出来。
注意取模求逆元!

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const ll mod=1e9+7; 5 ll n; 6 ll fpow(ll a,ll n) 7 { 8 ll res=1,base=a%mod; 9 while(n) 10 { 11 if(n&1) res*=base, res%=mod; 12 base*=base, base%=mod; 13 n>>=1; 14 } 15 return res%mod; 16 } 17 ll inv(ll a){return fpow(a,mod-2);} 18 int main() 19 { 20 int T; 21 cin>>T; 22 while(T--) 23 { 24 scanf("%I64d",&n); 25 ll ans=0; 26 ans+=fpow(n,4), ans%=mod; 27 ans+=6*fpow(n,3)%mod, ans%=mod; 28 ans+=11*fpow(n,2)%mod, ans%=mod; 29 ans+=6*n%mod, ans%=mod; 30 ans*=inv(24), ans%=mod; 31 printf("%I64d\n",ans); 32 } 33 }
I---Magic Potion【网络流】
题意:
有$n$个英雄,$m$只怪物。每个英雄可以杀某些指定的怪物,但是他们只能杀一次。现在有$k$瓶药水,喝了一瓶药水就可以多杀一只怪物,但是每个英雄最多只能喝一瓶。问他们最多可以杀多少怪物。
思路:
想dp想了半天想不出来。丢给zyn他直接就说是网络流。噢好有道理。
每个英雄和怪物之间有一条权值为1的边,源点和英雄有一个权值为1的边,怪物和汇点有权值唯一的边。
这样跑出来的最大流是不考虑喝药水的情况的答案。
现在可以喝药水了,相当于多了一个节点,源点到这个节点的边权值是k,然后这个节点和每个英雄有权值是1的边。
相当于给$k$个英雄多了一条1的流量,又限制了每个英雄只能喝一瓶。
听说Dinic T了,所以后来自己直接套的isap的板子。【其实还并不很熟网络流】

1 #include<iostream> 2 //#include<bits/stdc++.h> 3 #include<cstdio> 4 #include<cmath> 5 #include<cstdlib> 6 #include<cstring> 7 #include<algorithm> 8 #include<queue> 9 #include<vector> 10 #include<set> 11 #include<climits> 12 #include<map> 13 using namespace std; 14 typedef long long LL; 15 #define N 100010 16 #define pi 3.1415926535 17 #define inf 0x3f3f3f3f 18 19 const int maxn = 505; 20 int n, m, k; 21 struct edge{ 22 int v, w, nxt; 23 }e[maxn* maxn + 5 * maxn]; 24 int h[maxn * 2], tot; 25 int gap[maxn * 2], last[maxn * 2], d[maxn * 2], que[maxn * 2], ql, qr; 26 27 void addedge(int u, int v, int w) 28 { 29 e[++tot] = (edge){v, w, h[u]}; 30 h[u] = tot; 31 e[++tot] = (edge){u, 0, h[v]}; 32 h[v] = tot; 33 } 34 35 36 void init(int s, int t) 37 { 38 memset(gap, 0, sizeof(gap)); 39 memset(d, 0, sizeof(d)); 40 ++gap[d[t] = 1]; 41 for(int i = 1; i <= n + m + 3; i++){ 42 last[i] = h[i]; 43 } 44 que[ql = qr = 1] = t; 45 while(ql <= qr){ 46 int x = que[ql++]; 47 for(int i = h[x], v = e[i].v; i; i = e[i].nxt, v = e[i].v){ 48 if(!d[v]){ 49 ++gap[d[v] = d[x] + 1], que[++qr] = v; 50 } 51 } 52 } 53 } 54 55 int aug(int x, int s, int t, int mi) 56 { 57 if(x == t)return mi; 58 int flow = 0; 59 for(int &i = last[x], v = e[i].v; i; i = e[i].nxt, v = e[i].v){ 60 if(d[x] == d[v] + 1){ 61 int tmp = aug(v, s, t, min(mi, e[i].w)); 62 flow += tmp, mi -= tmp, e[i].w -= tmp, e[i ^ 1].w += tmp; 63 if(!mi)return flow; 64 } 65 } 66 if(!(--gap[d[x]]))d[s] = n + m + 4; 67 ++gap[++d[x]], last[x] = h[x]; 68 return flow; 69 } 70 71 int maxflow(int s, int t) 72 { 73 init(s, t); 74 int ret = aug(s, s, t, inf); 75 while(d[s] <= n + m + 3)ret += aug(s, s, t, inf); 76 return ret; 77 } 78 79 /*void addedge(int u,int v,int w) { 80 e[++tot]=(edge){v,w,h[u]}; 81 h[u]=tot; 82 e[++tot]=(edge){u,0,h[v]}; 83 h[v]=tot; 84 } 85 void init(int s,int t) { 86 memset(gap,0,sizeof gap),memset(d,0,sizeof d),++gap[d[t]=1]; 87 for (int i=1;i<=n + m + 3;++i) last[i]=h[i]; 88 que[ql=qr=1]=t; 89 while (ql<=qr) { 90 int x=que[ql++]; 91 for (int i=h[x],v=e[i].v;i;i=e[i].nxt,v=e[i].v) if (!d[v]) ++gap[d[v]=d[x]+1],que[++qr]=v; 92 } 93 } 94 int aug(int x,int s,int t,int mi) { 95 if (x==t) return mi; 96 int flow=0; 97 for (int &i=last[x],v=e[i].v;i;i=e[i].nxt,v=e[i].v) if (d[x]==d[v]+1) { 98 int tmp=aug(v,s,t,min(mi,e[i].w)); 99 flow+=tmp,mi-=tmp,e[i].w-=tmp,e[i^1].w+=tmp; 100 if (!mi) return flow; 101 } 102 if (!(--gap[d[x]])) d[s]=n + m + 4; 103 ++gap[++d[x]],last[x]=h[x]; 104 return flow; 105 } 106 int maxflow(int s,int t) { 107 init(s,t); 108 int ret=aug(s,s,t,inf); 109 while (d[s]<=n + m + 3) ret+=aug(s,s,t,inf); 110 return ret; 111 }*/ 112 113 int main() 114 { 115 while(scanf("%d%d%d", &n, &m, &k) != EOF){ 116 //init(1, n+ m + 3); 117 tot = 1; 118 memset(h, 0, sizeof(h)); 119 int s = 1, t = n + m + 3; 120 addedge(s, 2, k); 121 for(int i = 1; i <= n; i++){ 122 addedge(s, 2 + i, 1); 123 addedge(2, 2 + i, 1); 124 int t; 125 scanf("%d", &t); 126 for(int j = 0, mon; j < t; j++){ 127 scanf("%d", &mon); 128 addedge(2 + i, 2 + n + mon, 1); 129 } 130 } 131 for(int i = 1; i <= m; i++){ 132 addedge(2 + n + i, t, 1); 133 } 134 printf("%d\n", maxflow(s, t)); 135 } 136 137 return 0; 138 }
D---Country Meow【最小球覆盖】
题意:
三维空间中有$n$个点,现在要在空间中找一个点,使得他到这$n$个点最远的距离最小。
思路:
就是一个最小球覆盖的板子题。找的模拟退火的板子cf过不了了。
用的三分的板子直接就过了。

#include<iostream> //#include<bits/stdc++.h> #include<cstdio> #include<cmath> #include<cstdlib> #include<cstring> #include<algorithm> #include<queue> #include<vector> #include<set> #include<climits> #include<map> using namespace std; typedef long long LL; #define N 100010 #define pi 3.1415926535 #define inf 0x3f3f3f3f const int maxn = 105; const double eps = 1e-7; typedef struct {double p[3];}point; point a[maxn]; int n; double cal(point now) { double ans=0.0; for(int i=0;i<n;i++) ans=max(ans,sqrt((a[i].p[0]-now.p[0])*(a[i].p[0]-now.p[0])+(a[i].p[1]-now.p[1])*(a[i].p[1]-now.p[1])+(a[i].p[2]-now.p[2])*(a[i].p[2]-now.p[2]))); return ans; } point del(point now,int cnt) { if(cnt>=3) return now; double r=100000,l=-100000; double dr,dl; point tp1,tp2,ans1,ans2,ans; tp1=tp2=ans=now; while(r-l>eps) { dr=(2*r+l)/3; dl=(2*l+r)/3; tp1.p[cnt]=dl; tp2.p[cnt]=dr; ans1=del(tp1,cnt+1); ans2=del(tp2,cnt+1); if(cal(ans1)>cal(ans2)) { l=dl; ans=ans1; } else { r=dr; ans=ans2; } } return ans; } int main() { // freopen("t.txt","r",stdin); //ios::sync_with_stdio(false); //double ans; while(~scanf("%d", &n)) { for(int i=0; i<n; i++) //cin>>node[i].x>>node[i].y>>node[i].z; scanf("%lf%lf%lf",&a[i].p[0],&a[i].p[1],&a[i].p[2]); //minball(n); //cout<<ans<<endl; point ans; printf("%.7f\n",cal(del(ans, 0))); } return 0; }
K---Kangaroo Puzzle
题意:
思路:
这题代码可不能折叠啊。队友太强了!
1 #include<stdio.h> 2 #include<string.h> 3 #include <bits/stdc++.h> 4 5 using namespace std; 6 const int MAX_N = 10; 7 char c[4] = {'L', 'R', 'U', 'D'}; 8 9 int main() 10 { 11 int N, M; 12 cin >> N >> M; 13 string s; 14 for (int i = 1; i <= N; i++) 15 cin >> s; 16 int cnt = 0; 17 srand(56346275); 18 while (cnt++ < 50000) { 19 printf("%c", c[rand()%4]); 20 } 21 puts(""); 22 return 0; 23 }
M---Mediocre String Problem【manacher】【exKMP】
题意:
有一个串$S$,一个串$T$。现在要在$S$中选一段$S[i,j]$,和$T$中的$T[1,k]$拼起来是一串回文。问有多少种不同的三元组$(i,j,k)$
思路:
详细题解见:https://www.cnblogs.com/wyboooo/p/9982651.html

1 #include<iostream> 2 //#include<bits/stdc++.h> 3 #include<cstdio> 4 #include<cmath> 5 //#include<cstdlib> 6 #include<cstring> 7 #include<algorithm> 8 //#include<queue> 9 #include<vector> 10 //#include<set> 11 //#include<climits> 12 //#include<map> 13 using namespace std; 14 typedef long long LL; 15 #define N 100010 16 #define pi 3.1415926535 17 #define inf 0x3f3f3f3f 18 19 const int maxn = 1e6 + 5; 20 char s[maxn], ss[maxn * 2], t[maxn], s_rev[maxn]; 21 LL pre[maxn * 2]; 22 int lens, lent, p[maxn * 2]; 23 24 int init() 25 { 26 ss[0] = '$'; 27 ss[1] = '#'; 28 int lenss = 2; 29 for(int i = 0; i < lens; i++){ 30 ss[lenss++] = s[i]; 31 ss[lenss++] = '#'; 32 } 33 ss[lenss] = '\0'; 34 return lenss; 35 } 36 37 void manacher() 38 { 39 int lenss = init(); 40 int id, mx = 0; 41 for(int i = 1; i < lenss; i++){ 42 if(i < mx){ 43 p[i] = min(p[2 * id - i], mx - i); 44 } 45 else{ 46 p[i] = 1; 47 } 48 while(ss[i - p[i]] == ss[i + p[i]])p[i]++; 49 if(mx < i + p[i]){ 50 id = i; 51 mx = i + p[i]; 52 } 53 } 54 } 55 56 int nxt[maxn],ex[maxn]; //ex数组即为extend数组 57 //预处理计算next数组 58 void GETNEXT(char *str) 59 { 60 int i=0,j,po,len=strlen(str); 61 nxt[0]=len;//初始化next[0] 62 while(str[i]==str[i+1]&&i+1<len)//计算next[1] 63 i++; 64 nxt[1]=i; 65 po=1;//初始化po的位置 66 for(i=2;i<len;i++) 67 { 68 if(nxt[i-po]+i<nxt[po]+po)//第一种情况,可以直接得到next[i]的值 69 nxt[i]=nxt[i-po]; 70 else//第二种情况,要继续匹配才能得到next[i]的值 71 { 72 j=nxt[po]+po-i; 73 if(j<0)j=0;//如果i>po+nxt[po],则要从头开始匹配 74 while(i+j<len&&str[j]==str[j+i])//计算next[i] 75 j++; 76 nxt[i]=j; 77 po=i;//更新po的位置 78 } 79 } 80 } 81 //计算extend数组 82 void EXKMP(char *s1,char *s2) 83 { 84 int i=0,j,po,len=strlen(s1),l2=strlen(s2); 85 GETNEXT(s2);//计算子串的next数组 86 while(s1[i]==s2[i]&&i<l2&&i<len)//计算ex[0] 87 i++; 88 ex[0]=i; 89 po=0;//初始化po的位置 90 for(i=1;i<len;i++) 91 { 92 if(nxt[i-po]+i<ex[po]+po)//第一种情况,直接可以得到ex[i]的值 93 ex[i]=nxt[i-po]; 94 else//第二种情况,要继续匹配才能得到ex[i]的值 95 { 96 j=ex[po]+po-i; 97 if(j<0)j=0;//如果i>ex[po]+po则要从头开始匹配 98 while(i+j<len&&j<l2&&s1[j+i]==s2[j])//计算ex[i] 99 j++; 100 ex[i]=j; 101 po=i;//更新po的位置 102 } 103 } 104 } 105 106 107 int main() 108 { 109 110 while(scanf("%s", s) != EOF){ 111 scanf("%s", t); 112 lens = strlen(s); 113 lent = strlen(t); 114 for(int i = 0; i <= lens * 2 + 2; i++){ 115 pre[i] = 0; 116 p[i] = 0; 117 ex[i] = 0; 118 } 119 manacher(); 120 for(int i = lens * 2; i >= 2; i--){ 121 int x = i / 2; 122 pre[x]++; 123 pre[x - (p[i] / 2)]--; 124 } 125 for(int i = lens; i >= 1; i--){ 126 pre[i] += pre[i + 1]; 127 } 128 129 for(int i = 0; i <= lens; i++){ 130 s_rev[i] = s[lens - 1 - i]; 131 } 132 EXKMP(s_rev, t); 133 LL ans = 0; 134 /*for(int i = 1; i <= lens; i++){ 135 cout<<pre[i]<<" "<<ex[i]<<endl; 136 }*/ 137 for(int i = 1; i <= lens; i++){ 138 //if(ex[lens - i + 1]) 139 ans += 1LL * ex[lens - i + 1] * pre[i]; 140 } 141 printf("%I64d\n", ans); 142 } 143 return 0; 144 }
J---Prime Game【数论】
题意:
给定$n$个数,$fra(i,j)$表示第$i$个数到第$j$个数相乘的值的不同质因子个数,求$\sum_{i=1}^{n} \sum_{j=i}^{n}fra(i,j)$
思路:
预处理把区间内的所有质数筛出来。
然后枚举每个数的质因子,找到这个质因子对答案的贡献。
每次都找到这个质因子上一次出现的位置,那么他对这段区间都是有贡献的。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 typedef long long ll; 5 const int MAX_N = 1e6 + 5; 6 7 int prime[MAX_N+1]; 8 void getPrime() 9 { 10 memset(prime, 0, sizeof prime); 11 for (int i = 2; i <= MAX_N; i++) { 12 if (!prime[i]) prime[++prime[0]] = i; 13 for (int j = 1; j <= prime[0] && prime[j] <= MAX_N/i; j++) { 14 prime[i*prime[j]] = true; 15 if (i%prime[j] == 0) 16 break; 17 } 18 } 19 } 20 21 int a[MAX_N]; 22 int pre[MAX_N]; 23 int main() 24 { 25 getPrime(); 26 int N; 27 cin >> N; 28 memset(pre, 0, sizeof pre); 29 for (int i = 1; i <= N; i++) { 30 scanf("%d", a+i); 31 } 32 33 ll ans = 0; 34 for (int i = 1; i <= N; i++) { 35 for (int j = 1; prime[j] <= a[i]/prime[j]; j++) { 36 ll curp = prime[j]; 37 if (a[i] % prime[j] == 0) { 38 ll l = i - pre[curp]; 39 ll r = N-i+1; 40 ans += l*r; 41 pre[curp] = i; 42 while (a[i]%curp == 0) 43 a[i] /= curp; 44 } 45 } 46 if (a[i] > 1) { 47 ll curp = a[i]; 48 ll l = i - pre[curp]; 49 ll r = N-i+1; 50 ans += l*r; 51 pre[curp] = i; 52 while (a[i]%curp == 0) 53 a[i] /= curp; 54 } 55 } 56 cout << ans << endl; 57 return 0; 58 } 59 /* 60 10 61 99 62 10 47 53 9 83 33 15 24 62 */
A---Adrien and Austin【博弈论】
题意:
有$n$个石头并有编号,每次最多可以取$k$个最少取$1$个连续的石头,两个人轮流取,谁不能取了就输了。
思路:
刚开始没看到连续的,想半天都是错的。
如果是连续的话,情况就比较简单了。
先手对于任意的一段连续的$n$都可以把他取成大小相等的两段。后手在任意一段取,先手都可以在另一段对称的取。所以先手必胜。
当$n$是奇数,$k$是$1$的时候,先手没办法取出这样的两段。所以后手能赢。$n$为$0$后手也能赢。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 const int MAX_N = 1e6 + 5; 5 string s[2] = {"Adrien", "Austin"}; 6 7 8 int main() 9 { 10 int N, K; 11 cin >> N >> K; 12 if (N == 0) 13 cout << s[1] << endl; 14 else if (K == 1 && N%2 == 0) { 15 cout << s[1] << endl; 16 } 17 else { 18 cout << s[0] << endl; 19 } 20 return 0; 21 }



