网络流
优秀博客参考:http://www.cnblogs.com/Booble/archive/2011/03/04/1970453.html
https://blog.csdn.net/A_Comme_Amour/article/details/79356220
给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow).
好比你家是汇 自来水厂(有需要的同学可以把自来水厂当成银行之类 以下类似)是源
然后自来水厂和你家之间修了很多条水管子接在一起 水管子规格不一 有的容量大 有的容量小
然后问自来水厂开闸放水 你家收到水的最大流量是多少
如果自来水厂停水了 你家那的流量就是0 当然不是最大的流量
但是你给自来水厂交了100w美金 自来水厂拼命水管里通水 但是你家的流量也就那么多不变了 这时就达到了最大流
三条基本性质:
容量限制:边的流量小于等于边的容量
流量守恒:除了源和汇之外的任一节点,流出的等于流入的
斜对称性:x向y流了F, y就向x流了-F
三种网络 容量网络&流量网络残留网络
容量网络就是关于容量的网络 基本是不改变的(极少数问题需要变动)
流量网络就是关于流量的网络 在求解问题的过程中
通常在不断的改变 但是总是满足上述三个性质
调整到最后就是最大流网络 同时也可以得到最大流值
残留网络往往概括了容量网络和流量网络 是最为常用的
残留网络=容量网络-流量网络
这个等式是始终成立的 残留值当流量值为负时甚至会大于容量值
流量值为什么会为负?有正必有负,记住斜对称性!
算法:
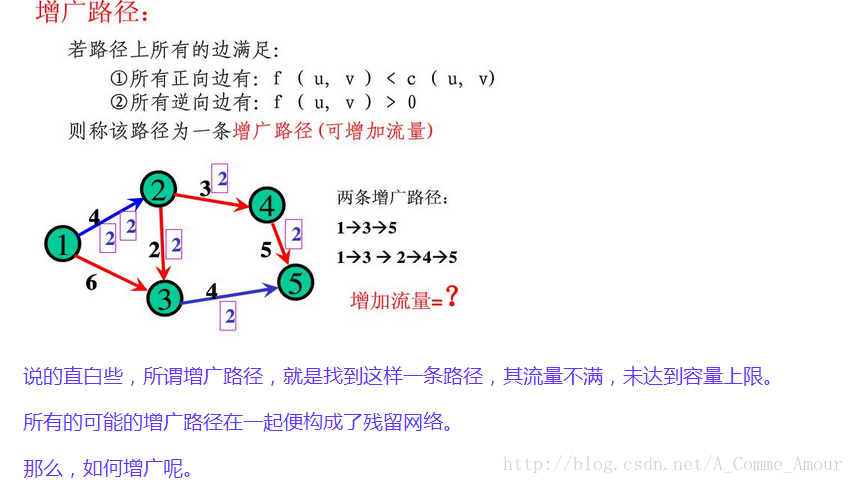
求解网络流的基本思想就是每次寻找增广路(就是源点到汇点的一条可行路)
然后ans+=增广路能流过的流量,更新剩余网络,然后再做增广路,直到做不出增广路。
关于网络流入门最难理解的地方就是剩余网络了....为什么在找到一条增广路后...不仅要将每条边的可行流量减去增广路能流过的流量...还要将每条边的反向弧加上增广路能流过的流量.?..原因是在做增广路时可能会阻塞后面的增广路...或者说做增广路本来是有个顺序才能找完最大流的.....但我们是任意找的...为了修正...就每次将流量加在了反向弧上...让后面的流能够进行自我调整...剩余网络的更新(就在原图上更新就可以了)
下面是所有最大流算法的精华部分:引入反向边
为什么要有反向边呢? 
我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。于是我们修改后得到了下面这个流。(图中的数字是容量) 
这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个”后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时,inc(c[y,x],delta)
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下
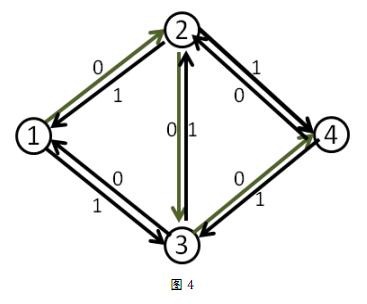
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。

那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
Ford-Fulkerson算法&Edmonds-Karp 最短增广路算法
在每次增广的时候,选择从源到汇的具有最少边数的增广路径,也就是说!不是通过dfs寻找增广路径,而是通过bfs寻找增广路径。
这就是Edmonds-Karp 最短增广路算法
已经证明这种算法的复杂度上限为nm2 (n是点数,m是边数)
queue <int> q;
int n,m,x,y,s,t,g[201][201],pre[201],flow[201],maxflow;
//g邻接矩阵存图,pre增广路径中每个点的前驱,flow源点到这个点的流量
inline int bfs(int s,int t)
{
while (!q.empty()) q.pop();
for (int i=1; i<=n; i++) pre[i]=-1;
pre[s]=0;
q.push(s);
flow[s]=INF;
while (!q.empty())
{
int x=q.front();
q.pop();
if (x==t) break;
for (int i=1; i<=n; i++)
//EK一次只找一个增广路
if (g[x][i]>0 && pre[i]==-1)
{
pre[i]=x;
flow[i]=min(flow[x],g[x][i]);
q.push(i);
}
}
if (pre[t]==-1) return -1;
else return flow[t];
}
//increase为增广的流量
void EK(int s,int t)
{
int increase=0;
while ((increase=bfs(s,t))!=-1)//这里的括号加错了!Tle
{//迭代
int k=t;
while (k!=s)
{
int last=pre[k];//从后往前找路径
g[last][k]-=increase;
g[k][last]+=increase;
k=last;
}
maxflow+=increase;
}
}
int main()
{
scanf("%d%d",&m,&n);
for (int i=1; i<=m; i++)
{
int z;
scanf("%d%d%d",&x,&y,&z);
g[x][y]+=z;//此处不可直接输入,要+=
}
EK(1,n);
printf("%d",maxflow);
return 0;
}
Dinic算法
dinic算法在EK算法的基础上增加了分层图的概念,根据从s到各个点的最短距离的不同,把整个图分层。寻找的增广路要求满足所有的点分别属于不同的层,且若增广路为s,P1,P2…Pk,t,点v在分层图中的所属的层记为deepv,那么应满足deeppi=deeppi−1+1
- 先利用BFS对残余网络分层
一个节点的深度,就是源点到它最少要经过的边数。 -
利用BFS对残余网络分层,分完层后,利用DFS从前一层向后一层反复寻找增广路。
- 分完层后,从源点开始,用DFS从前一层向后一层反复寻找增广路(即要求DFS的每一步都必须要走到下一层的节点)。
因此,前面在分层时,只要进行到汇点的层次数被算出即可停止,因为按照该DFS的规则,和汇点同层或更下一层的节点,是不可能走到汇点的。 -
DFS过程中,要是碰到了汇点,则说明找到了一条增广路径。此时要增加总流量的值,消减路径上各边的容量,并添加反向边,即所谓的进行增广。
-
DFS找到一条增广路径后,并不立即结束,而是回溯后继续DFS寻找下一个增广路径。
回溯到哪个节点呢?
回溯到的节点u满足以下条件:- DFS搜索树的树边(u,v)上的容量已经变成0。即刚刚找到的增广路径上所增加的流量,等于(u,v)本次增广前的容量。(DFS的过程中,是从u走到更下层的v的)
- u是满足条件 1)的最上层的节点如果回溯到源点而且无法继续往下走了,DFS结束。
因此,一次DFS过程中,可以找到多条增广路径。
- DFS结束后,对残余网络再次进行分层,然后再进行DFS当残余网络的分层操作无法算出汇点的层次(即BFS到达不了汇点)时,算法结束,最大流求出。
- 分完层后,从源点开始,用DFS从前一层向后一层反复寻找增广路(即要求DFS的每一步都必须要走到下一层的节点)。
ps要求出最大流中每条边的流量,怎么办?
将原图备份,原图上的边的容量减去做完最大流的残余网络上的边的剩余容量,就是边的流量。
时间复杂度
在普通情况下, DINIC算法时间复杂度为O(V2E)
在二分图中, DINIC算法时间复杂度为O(√VE)多路增广
每次不是寻找一条增广路,而是在DFS中,只要可以就递归增广下去,实际上形成了一张增广网。
• 当前弧优化
对于每一个点,都记录上一次检查到哪一条边。因为我们每次增广一定是彻底增广(即这条已经被增广过的边已经发挥出了它全部的潜力,不可能再被增广了),下一次就不必再检查它,而直接看第一个未被检查的边。
优化之后渐进时间复杂度没有改变,但是实际上能快不少。
实际写代码的时候要注意,head数组初始值为-1,存储时从0开始存储,这样在后面写反向弧的时候比较方便,直接异或即可。
关于复制head的数组cur;目的是为了当前弧优化。已经增广的边就不需要再走了.
int n,m,x,y,z,maxflow,deep[500];//deep深度
struct Edge{
int next,to,dis;
}edge[500];
int num_edge=-1,head[500],cur[500];//cur用于复制head
queue <int> q;
void add_edge(int from,int to,int dis,bool flag)
{
edge[++num_edge].next=head[from];
edge[num_edge].to=to;
if (flag) edge[num_edge].dis=dis;//反图的边权为 0
head[from]=num_edge;
}
//bfs用来分层
bool bfs(int s,int t)
{
memset(deep,0x7f,sizeof(deep));
while (!q.empty()) q.pop();
for (int i=1; i<=n; i++) cur[i]=head[i];
deep[s]=0;
q.push(s);
while (!q.empty())
{
int now=q.front(); q.pop();
for (int i=head[now]; i!=-1; i=edge[i].next)
{
if (deep[edge[i].to]>inf && edge[i].dis)//dis在此处用来做标记 是正图还是返图
{
deep[edge[i].to]=deep[now]+1;
q.push(edge[i].to);
}
}
}
if (deep[t]<inf) return true;
else return false;
}
//dfs找增加的流的量
int dfs(int now,int t,int limit)//limit为源点到这个点的路径上的最小边权
{
if (!limit || now==t) return limit;
int flow=0,f;
for (int i=cur[now]; i!=-1; i=edge[i].next)
{
cur[now]=i;
if (deep[edge[i].to]==deep[now]+1 && (f=dfs(edge[i].to,t,min(limit,edge[i].dis))))
{
flow+=f;
limit-=f;
edge[i].dis-=f;
edge[i^1].dis+=f;
if (!limit) break;
}
}
return flow;
}
void Dinic(int s,int t)
{
while (bfs(s,t))
maxflow+=dfs(s,t,inf);
}
int main()
{
// for (int i=0; i<=500; i++) edge[i].next=-1;
memset(head,-1,sizeof(head));
scanf("%d%d",&m,&n);
for (int i=1; i<=m; i++)
{
scanf("%d%d%d",&x,&y,&z);
add_edge(x,y,z,1); add_edge(y,x,z,0);
}
Dinic(1,n);
printf("%d",maxflow);
return 0;
}ISAP算法
也是基于分层思想的最大流算法。所不同的是,它省去了Dinic每次增广后需要重新构建分层图的麻烦,而是在每次增广完成后自动更新每个点的『标号』(也就是所在的层)
最短增广路算法是一种运用距离标号使寻找增广路的时间复杂度下降的算法。所谓的距离标号就是某个点到汇点的最少的弧的数量(即当边权为1时某个点的最短路径长度). 设点i的标号为d[i], 那么如果将满足d[i] = d[j] + 1, 且增广时只走允许弧, 那么就可以达到”怎么走都是最短路”的效果. 每个点的初始标号可以在一开始用一次从汇点沿所有反向的BFS求出.
- 定义节点的标号为到汇点的最短距离;
- 每次沿可行边进行增广, 可行边即: 假设有两个点 i, j 若 d[i] = 3, d[j] = 4, 则d[j] = d[i] + 1, 也就是从 j 到 i 有一条边.
- 找到增广路后,将路径上所有边的流量更新.
- 遍历完当前结点的可行边后更新当前结点的标号为 d[now] = min( d[next] , add_flow(now,next) > 0)+1,使下次再搜的时候有路可走。
- 图中不存在增广路后即退出程序,此时得到的流量值就是最大流。
需要注意的是, 标号的更新过程首先我们要理解更新标号的目的。标号如果需要更新,说明在当前的标号下已经没有增广路可以继续走,这时更新标号就可以使得我们有继续向下走的可能,并且每次找的都是能走到的点中标号最小的那个点,这样也使得每次搜索长度最小.
GAP 优化
由于可行边定义为:(now,next) | h[now] = h[next]+1,所以若标号出现“断层”即有的标号对应的顶点个数为0,则说明剩余图中不存在增广路,此时便可以直接退出,降低了无效搜索。举个栗子:若结点标号为3的结点个数为0,而标号为4的结点和标号为2的结点都大于 0,那么在搜索至任意一个标号为4的结点时,便无法再继续往下搜索,说明图中就不存在增广路。此时我们可以以将 h[1]=n 形式来变相地直接结束搜索
时间复杂度
渐进时间复杂度和dinic相同,但是非二分图的情况下isap更具优势。
queue <int> q;
int m,n,x,y,z,maxflow,head[5000],num_edge=-1;
int cur[5000],deep[5000],last[5000],num[5000];
//cur当前弧优化; last该点的上一条边; num桶 用来GAP优化
struct Edge{
int next,to,dis;
}edge[500];
void add_edge(int from,int to,int dis,bool flag)
{
edge[++num_edge].next=head[from];
edge[num_edge].to=to;
edge[num_edge].dis=dis;
head[from]=num_edge;
}
//bfs仅用于更新deep
void bfs(int t)
{
while (!q.empty()) q.pop();
for (int i=0; i<=m; i++) cur[i]=head[i];
for (int i=1; i<=n; i++) deep[i]=n;
deep[t]=0;
q.push(t);
while (!q.empty())
{
int now=q.front(); q.pop();
for (int i=head[now]; i!=-1; i=edge[i].next)
{
if (deep[edge[i].to]==n && edge[i^1].dis)//i^1是为了找反边
{
deep[edge[i].to]=deep[now]+1;
q.push(edge[i].to);
}
}
}
}
int add_flow(int s,int t)
{
int ans=inf,now=t;
while (now!=s)
{
ans=min(ans,edge[last[now]].dis);
now=edge[last[now]^1].to;
}
now=t;
while (now!=s)
{
edge[last[now]].dis-=ans;
edge[last[now]^1].dis+=ans;
now=edge[last[now]^1].to;
}
return ans;
}
void isap(int s,int t)
{
int now=s;
bfs(t);//搜出一条增广路
for (int i=1; i<=n; i++) num[deep[i]]++;
while (deep[s]<n)
{
if (now==t)
{//如果到达汇点就直接增广,重新回到源点进行下一轮增广
maxflow+=add_flow(s,t);
now=s;//回到源点
}
bool has_find=0;
for (int i=cur[now]; i!=-1; i=edge[i].next)
{
if (deep[now]==deep[edge[i].to]+1 && edge[i].dis)//找到一条增广路
{
has_find=true;
cur[now]=i;//当前弧优化
now=edge[i].to;
last[edge[i].to]=i;
break;
}
}
if (!has_find)//没有找到出边,重新编号
{
int minn=n-1;
for (int i=head[now]; i!=-1; i=edge[i].next)//回头找路径
if (edge[i].dis)
minn=min(minn,deep[edge[i].to]);
if ((--num[deep[now]])==0) break;//GAP优化 出现了断层
num[deep[now]=minn+1]++;
cur[now]=head[now];
if (now!=s)
now=edge[last[now]^1].to;
}
}
}
int main()
{
memset(head,-1,sizeof(head));
scanf("%d%d",&m,&n);
for (int i=1; i<=m; i++)
{
scanf("%d%d%d",&x,&y,&z);
add_edge(x,y,z,1); add_edge(y,x,z,0);
}
isap(1,n);
printf("%d",maxflow);
return 0;
}EK处理在运算过程中需要不断加边的最大流比SAP更有优势
引申问题:最小费用流
有一个流量网络,现在每个边除了流量,现在还有一个单位费用,这条边的费用相当于它的单位费用乘上它的流量,我们要保持最大流的同时,还要保持边权最小,这就是最小费用最大流问题。
总增广的费用就是最短路*总流量
算法:将dinic中的bfs改为spfa
bool vis[maxn];
int n,m,s,t,x,y,z,f,dis[maxn],pre[maxn],last[maxn],flow[maxn],maxflow,mincost;
//dis最小花费;pre每个点的前驱;last每个点的所连的前一条边;flow源点到此处的流量
struct Edge{
int to,next,flow,dis;//flow流量 dis花费
}edge[maxn];
int head[maxn],num_edge;
queue <int> q;
void add_edge(int from,int to,int flow,int dis)
{
edge[++num_edge].next=head[from];
edge[num_edge].to=to;
edge[num_edge].flow=flow;
edge[num_edge].dis=dis;
head[from]=num_edge;
}
bool spfa(int s,int t)
{
memset(dis,0x7f,sizeof(dis));
memset(flow,0x7f,sizeof(flow));
memset(vis,0,sizeof(vis));
q.push(s); vis[s]=1; dis[s]=0; pre[t]=-1;
while (!q.empty())
{
int now=q.front();
q.pop();
vis[now]=0;
for (int i=head[now]; i!=-1; i=edge[i].next)
{
if (edge[i].flow>0 && dis[edge[i].to]>dis[now]+edge[i].dis)//正边
{
dis[edge[i].to]=dis[now]+edge[i].dis;
pre[edge[i].to]=now;
last[edge[i].to]=i;
flow[edge[i].to]=min(flow[now],edge[i].flow);//
if (!vis[edge[i].to])
{
vis[edge[i].to]=1;
q.push(edge[i].to);
}
}
}
}
return pre[t]!=-1;
}
void MCMF()
{
while (spfa(s,t))
{
int now=t;
maxflow+=flow[t];
mincost+=flow[t]*dis[t];
while (now!=s)
{//从源点一直回溯到汇点
edge[last[now]].flow-=flow[t];//flow和dis容易搞混
edge[last[now]^1].flow+=flow[t];
now=pre[now];
}
}
}
int main()
{
memset(head,-1,sizeof(head)); num_edge=-1;//初始化
scanf("%d%d%d%d",&n,&m,&s,&t);
for (int i=1; i<=m; i++)
{
scanf("%d%d%d%d",&x,&y,&z,&f);
add_edge(x,y,z,f); add_edge(y,x,0,-f);
//反边的流量为0,花费是相反数
}
MCMF();
printf("%d %d",maxflow,mincost);
return 0;
}引申问题:最小割
最大流最小割定理(Maximum Flow, Minimum Cut Theorem):
1. 最小割等价于最大流。
2. 最小割在最大流中一定是满流边,是增广路径中容量最小的边。
3. 一条增广路径只对应一条最小割。(如果一条增广路中两条满流且都需要割掉,那一定通过反向边分成两条增广路)
最小割在最大流中一定是满流边,其实就是S到T之间必须经过的边(不管确定与否)。只要找到一条增广路径,就必须经过一条最小割。最小割中的边饱和就再也不能找到增广路径。
一条最小割可以对应多条增广路径,但是一条增广路径只能对应一条最小割(或最小割的可能性)。
求最小割其实就是一条增广路径中容量最小的边,这恰好与最大流的求解是一致的。
Stoer_Wagner算法
求无向图全局最小割
算法复杂度为O(n3)。如果在prim中加堆优化,复杂度会降为O(n2logn)。
主要思想是先找任意2点的最小割,然后记录下这个最小割,再合并这2个点。这样经过n−1次寻找任意2点最小割,每次更新全局最小割,最后整张图缩成一个点,算法结束,所保存下来的最小割就是全局最小割。
int n,m,mp[maxn][maxn],v[maxn],dis[maxn];
//mp图,v[i]表示i节点合并到的顶点;dis[i] i点到A集合中所有的点的长度之和
bool vis[maxn];//是否进入集合A
int SW(int n)
{
int ans=inf;
for (int i=0; i<n; i++) v[i]=i;//顶点定为自己
while (n>1)
{
int k=1,pre=0;//k保存最大dis值的下标 pre上一次选入集合的点
//每次使0为第一个加入的点
for (int i=1; i<n; i++)
{
dis[v[i]]=mp[v[0]][v[i]];
if (dis[v[i]]>dis[v[k]]) k=i;
}
memset(vis,0,sizeof(vis));
vis[v[0]]=1;//标记进入集合
for (int i=1; i<n; i++)
{
if (i==n-1)//最后一次加入,更新答案
{
ans=min(ans,dis[v[k]]);
for (int j=0; j<n; j++)
{
mp[v[pre]][v[j]] += mp[v[j]][v[k]];
mp[v[j]][v[pre]] += mp[v[j]][v[k]];
}
v[k]=v[--n];//删除最后一个点
}
vis[v[k]]=1;
pre=k;
k=-1;
for (int j=0; j<n; j++)
if (!vis[v[j]])
{
//将上一次求的k加入集合
dis[v[j]]+=mp[v[pre]][v[j]];
if (k==-1 || dis[v[j]]>dis[v[k]])
k=j;
}
}
}
return ans;
}
int main()
{
while (~scanf("%d%d",&n,&m))
{
memset(mp,0,sizeof(mp));
int x,y,z;
for (int i=1; i<=m; i++)
{
scanf("%d%d%d",&x,&y,&z);
mp[x][y]+=z; mp[y][x]+=z;
}
printf("%d\n",SW(n));
}
return 0;
}