Improving Contrastive Learning by Visualizing Feature Transformation【ICCV21Oral】【阅读笔记】

目前正负样本的构造和选择大部分还是采用数据增强，依赖于人的经验和直觉，可能并不是有效的，也缺少可解释性。

本文在特征层面进行data manipulation来提供更加explainable和effective的正负样本。
首先，观察训练过程中anchor/positive以及anchor/negative对之间的相似度变化
然后，通过改变MoCo中的momentum值，观察相似度变化对性能的影响
最后基于上述观察，提出针对正样本的extrapolation操作和针对负样本的interpolation操作。

实际上作者说了一堆，在代码层面具体只是改动了InfoNCE loss的计算公式。

对比学习流程

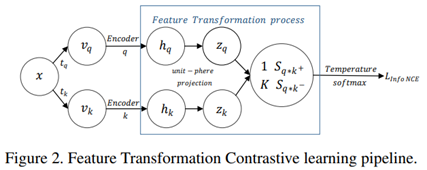
anchor x经过两个不同的数据增强\(𝑡_𝑞,𝑡_𝑘\)，分别会得到两个view，构成了正样本。然后经过两个encoder分别映射到不同的特征空间，最后用L2 norm规范化到unit sphere得到\(𝑧_𝑞,𝑧_𝑘\). 用\(z_q,z_k\)计算内积得到余弦相似度，也就是对应的positive pair score \(S_{q\cdot k^+}\) 和K个negative pair score \(S_{q\cdot k^-}\).用这些score计算得到InfoNCE loss：$$L = -log[\frac{exp(S_{q\cdot k^+}/\tau)}{exp({S_{q\cdot k^+}/\tau})+\sum_Kexp(S_{q\cdot k^-}/\tau)}]$$
文章中所指的特征变换的过程就是对encoder的embedding进行操作的过程，目前最常用的就是L2规范化。文章当中选取了正负样本对的score进行可视化。一个原因是可视化InfoNCE的输入对可以帮助理解对比学习的过程；另一个原因是特征是高维的，不利于观察样本特性，而score是一维且值域在[-1,1]。

Visualization with MoCo

使用MoCo架构进行可视化。
首先通过调整momentum参数对性能的影响。随着m的减小（encoder更新速度增加），准确率呈现倒U型趋势。

Neg score

而在对score分布数据的可视化中可以看到，m变小，encoder更新速度增大，每个training step中的特征变化变快，负样本队列中negative score的variance（或称为incosistency）变大。variance相对比较稳定效果比较好。

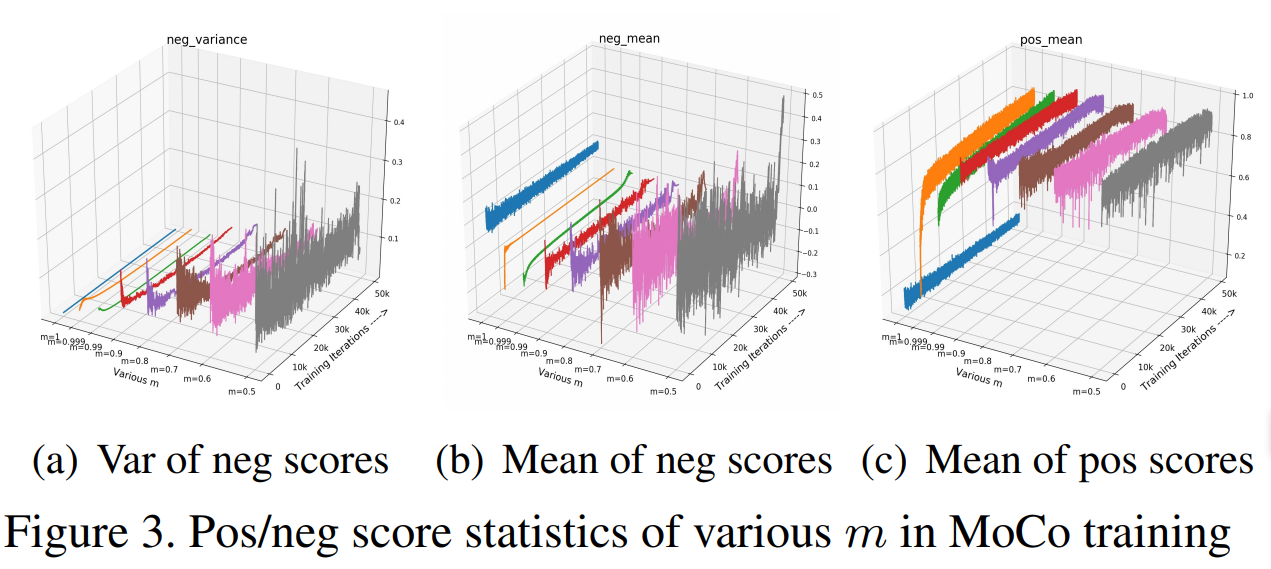
neg score的均值反应的时memory queue中所有负样本的approximate score。如果他在训练过程中剧烈波动，那么对应的损失函数和梯度也会剧烈波动，就会导致不收敛。

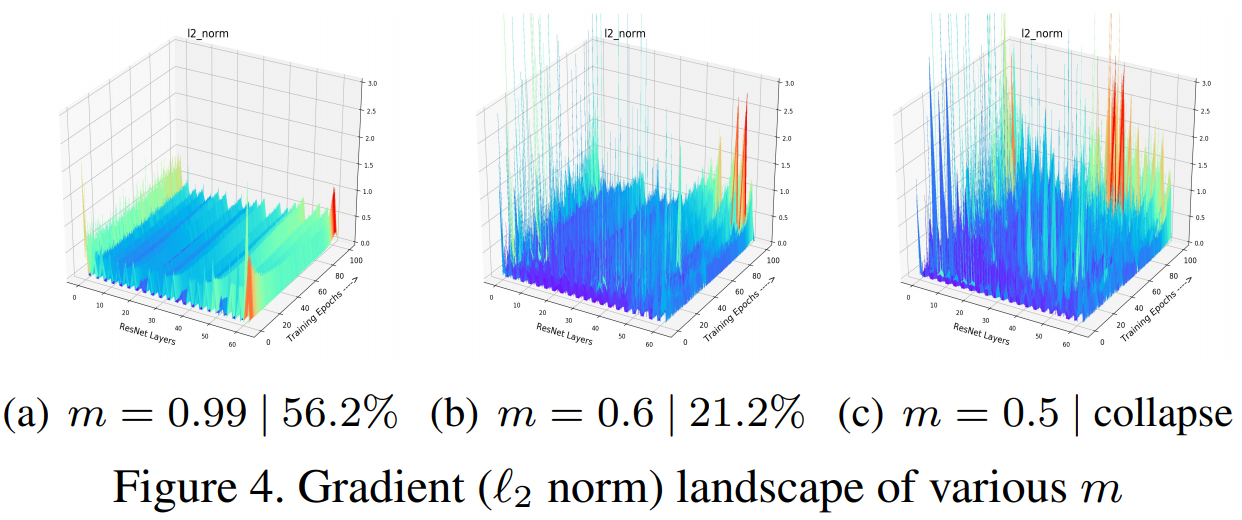
总的来说，要训练一个更好的pre-trained模型，和有监督学习也是类似的，需要使训练过程中梯度以及负样本在分数分布上保持稳定性和光滑性。

Pos score

比较小的m不仅表示的使更快的更新速度，还表示encoder之间具有更大的相似度。encoder之间越相似，那么\(z_q\)和\(z_{k^+}\)之间不相似度越低，只留下了数据增强所带来的view variance，positive score相对比较高。通过增大m，可以得到harder positive，transfer准确度也提高。实际上这和InfoMin原则使匹配的，提升view variance，增加互信息，那么encoder学到的embedding就更鲁棒。

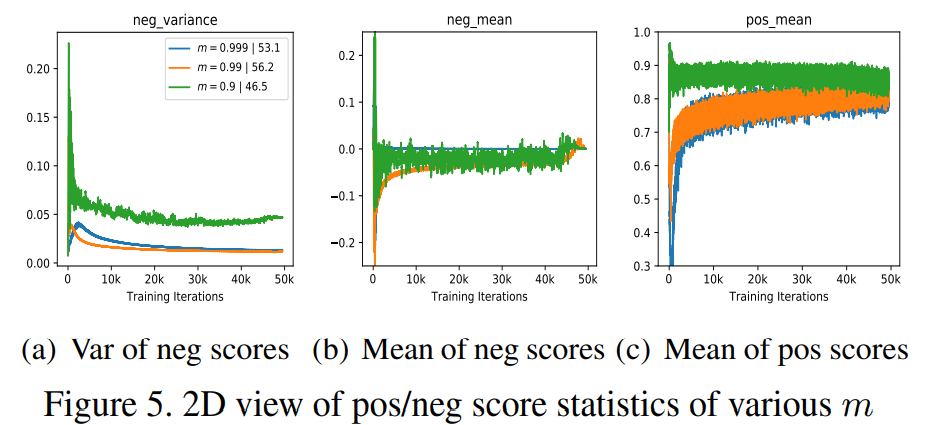
为了得到稳定光滑的score分布和梯度，使用一些特征变换减小positive score得到harder positives。

特征变换

InfoNCE的目标是在特征空间拉近anchor和正样本的距离，推远他和负样本的距离。因此可以直接在pos/neg样本特征上进行特征变换，提供更加合适的正则化或是让学习过程更困难。具体到本文，对于正样本作者设计了extrapolation来增加正样本的难度，用interpolation增加负样本的多样性。作者在文中指明，这样的操作并不是更改了loss项，而是改变了原来计算loss时使用的score。

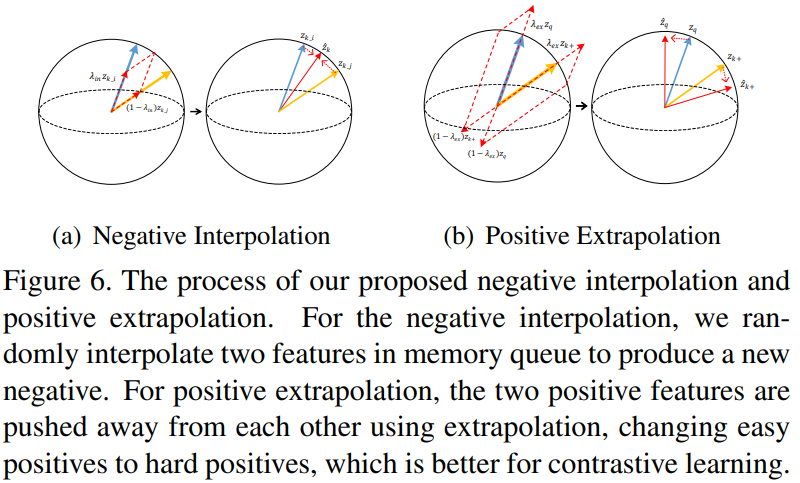
Positive Extrapolation

前面已经通过可视化说明了，降低positive score可以得到难正样本，对训练结果有益。因此希望找到一种方式直接变换特征，使他们之间的view variance在训练过程中增加。

首先用加权和的方式生成新特征：

\[\widehat{z}_q = \lambda_{ex}z_q+(1-\lambda_{ex})z_{k^+} \]

\[\widehat{z}_{k^+} = \lambda_{ex}z_{k^+}+(1-\lambda_{ex})z_q \]

这里参考Mixup的思想，让两个权值和为1.同时我们希望新的到的特征的pos score \(\widehat{S}_{q\cdot k^+}\)要小于原score \(S_{q\cdot k^+}\)：

\[\widehat{S}_{q\cdot k^+}=2\lambda_{ex}(1-\lambda_{ex})(1-S_{q\cdot k^+})+S_{q\cdot k^+}\leq S_{q\cdot k^+} \]

为了保证上式成立，需要满足\(\lambda_{ex}\geq1\).因此作者在文章从Beta分布中采样得到\(\lambda_{ex}\backsim Beta(\alpha_{ex}, \alpha_{ex})+1\)

在实验中发现，当\(\alpha_{ex} < 1\)时，会容易采样得到极大或极小的\(\lambda_{ex}\)，带来过多或过少的hardness，效果不如\(\alpha_{ex} > 1\)，此时 \(\lambda_{ex}=1.5\)概率比较高。

Negative Interpolation

定义MoCo中的负样本队列为\(Z_{neg}={z_1, z_2, ..., z_K}\)， \(Z_{perm}\)是队列的随机排列。对两个队列进行插值得到新的队列

\[\widehat{Z}_{neg}=\lambda_{in}\cdot Z_{neg}+(1-\lambda_{in})\cdot Z_{perm} \]

\[\lambda_{in}\backsim Beta(\alpha_{in}, \alpha_{in}) \]

对队列随机排列以及\(\lambda_{in}\)保证了训练中负样本队列的多样性。实际上是提升了sample variance（diversity）。这种方式并不是简单的扩展队列中的负样本数，也不是图像级的mixup。

Discussion

作者在实验中比较了几个问题：

• FT和扩展负样本数目：
  之前的工作说明了负样本数目增加是有利于表现的，因为可以提升互信息的下界。实际上文中提出的negative interpolation也可以看作是一种增加负样本的方式。实验比较了\(Z_{neg}(K), Z_{neg}(2K), \widehat{Z}_{neg}, \widetilde{Z}_{neg}(\widehat{Z}_{neg}\bigcup Z_{neg})\)
  
  根据这个实验结果可以看到，\(\widetilde{Z}_{neg}\)比\(\widehat{Z}_{neg}\)要好0.09%，而同样增加相同的负样本数\(Z_{neg}(2K)\)比\(Z_{neg}(K)\)要好0.3%。同时\(\widehat{Z}_{neg}\)比\(Z_{neg}(2K)\)要好3.24%，说明\(\widehat{Z}_{neg}\)中有很强的多样性。

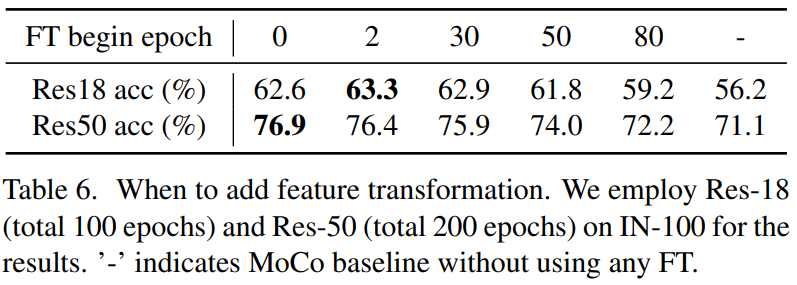
• 加入FT的时机：
  
  可以看到在不同阶段加入FT都是有效的，在比较早的阶段加入效果更好。

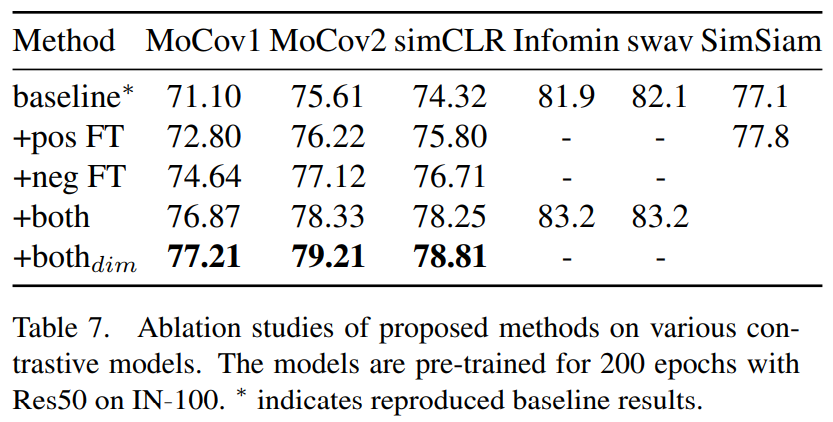
• Dimension-level mixing：
  考虑\(\lambda\)是一个向量而不是一个标量，对不同的维度用不同的参数控制加权的比例。
  
  可以看到不论是pos还是neg，这样的效果都要更好。

• FT带来的增益是否可以被更长的训练时间抵消
  训练时间边长可以缩小FT带来的improvement，因为训练时间变长意味着可以比较更多的正负样本。但是FT可以加速这个过程，给出更丰富的多样性让结果更快收敛。