Attention in Super-Resolution[阅读笔记][RCAN][SAN][HAN]
今天总结一下目前SR的SOTA中利用了Attention的工作,主要有3篇.按时间顺序分别是18年的RCAN,19年的SAN和20年的HAN.利用Attention的SR再PSNR表现上都排名比较靠前,HAN可以算是目前表现排在第一的.
RCAN【ECCV18】

浅层特征提取,用一层卷积$$F_0=H_{SF}(I_{LR})$$
RIR是达到目前最深的深度(超过400层卷积),提供了非常大的感受野。
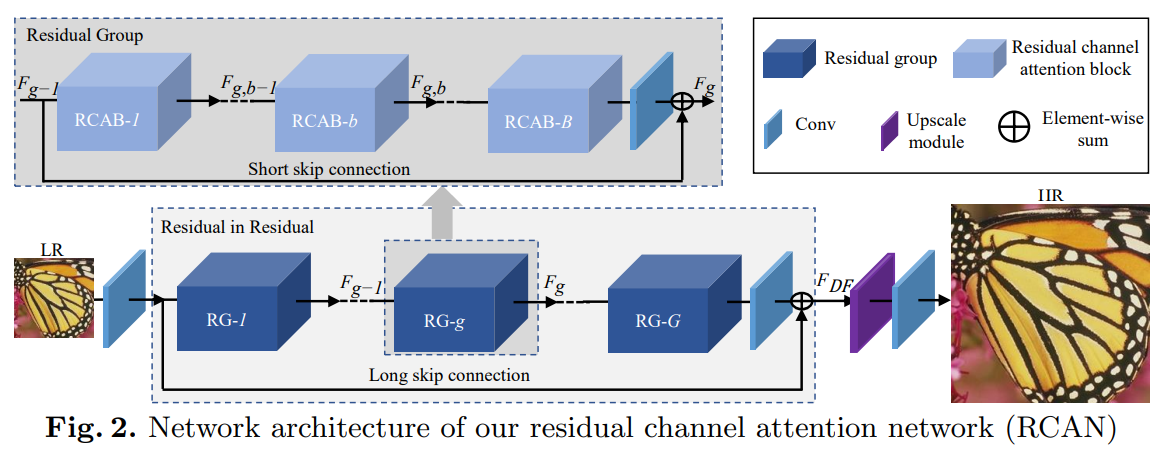
Residual in Residual
包含G个residual group(RG)和长跳连接(LSC)。每一个RG包含B个residual channel attention模块(RCAB)和短跳连接(SSC)。
第g个RG的特征为:$$F_g=H_g(F_{g-1})=H_g(H_{g-1}(...H_1(F_0)...))$$
长跳连接解决的是RIR结构深度过深时训练稳定性的问题,并且通过残差学习提升表现。
其中\(W_{LSC}\)是RIR结构末尾卷积的权重,这里出于简便性不考虑bias term。
第g个RG中第b个RCAB的特征为:
每个模块都包含一个短跳连接
Channel Attention
考虑到每一个filter都只有一个局部的感受野,这里使用global average pooling得到channel-wise global spatial information。
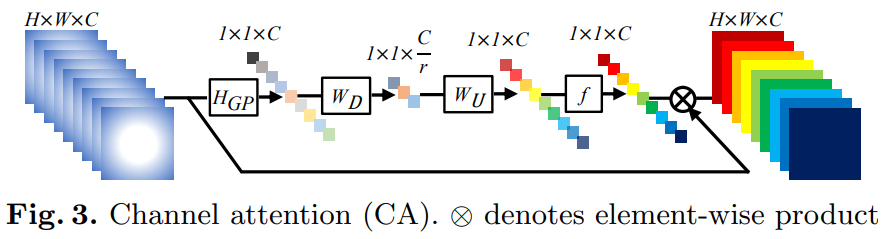
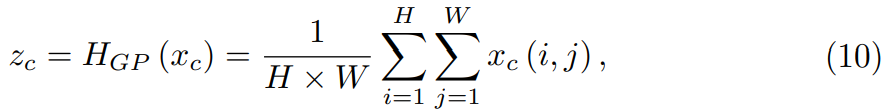
\(f(\cdot),\sigma(\cdot)\)表示sigmoid 和ReLU函数.低维特征先经过reduction ratio为r的channel-downscaling模块,再经过ReLU激活后,通过ratio为r的channel-upscaling模块.最后得到channel统计量s,用来rescale输入x
Residual Channel Attention Block(RCAB)
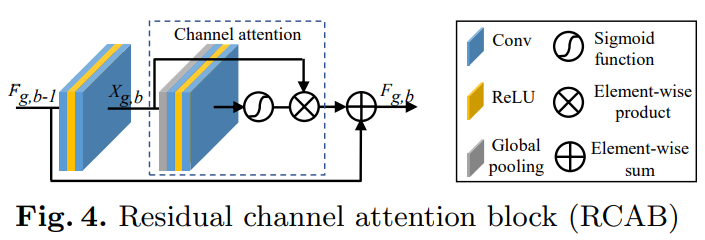
其中\(R_{g,b}\)是channel attention函数,\(W_{g,b}^1, W_{g,b}^2\)是RCAB中两个卷积的权重.
SAN【CVPR19】

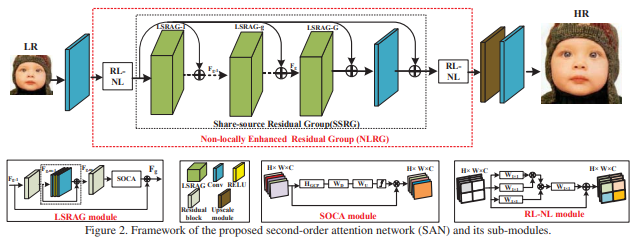
网络总体分为四个部分:浅层特征提取,基于NLRG的深层特征提取,upscale模块,重建
浅层特征由一层卷积提取:\(F_0=H_{SF}(I_{LR})\),其中\(H_{SF}(\cdot)\)是卷积操作。
深层特征\(F_{DF}=H_{NLRG}(F_0)\),包含几个non-local模块和G个local-source residual attention group(LSRAG)模块。
重建特征\(F_{\uparrow}=H_{\uparrow}(F_{DF})\),\(H_{\uparrow}\)可以是transposed conv或ESPCN
最后\(I_{SR}=H_R(F_\uparrow)=H_{SAN}(I_{LR})\)
NLRG
包含几个region-level non-local(RL-NL)模块和一个share-source residual group(SSRG)结构。SSRG由G个LSRAG with SSC组成,LSRAG包含M个residual blocks with local-source skip connection+SOCA。
第g个group的LSRAG: \(F_g=W_{SSC}F_0+H_g(F_{g-1})\),\(W_{SSC}\)是给浅层特征的conv层的权重,初始化为0,再逐步给浅层特征更多权重。
最终得到的\(F_{DF}=W_{SSC}F_0+F_G\)
RL-NL
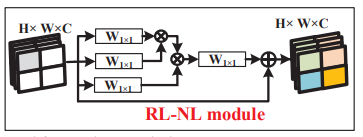
全局non-local模块的缺点是:计算量过大,特别是当特征图尺寸很大的时候;Non-Local Recurrent Network for Image Restoration中说明了,在低层视觉领域选择合适的邻域大小进行non-local效果更好。因此首先将输入划分为\(k\times k\)
LSRAG
类似于RCAN中的residual group,由多个残差模块+SOCA组成
SOCA
均值、最值为一阶统计量,协方差矩阵为二阶统计量。本文的方法基本和下面MPN-COV的方法差不多。
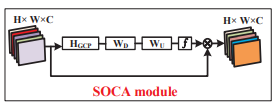
首先进行协方差规范化,将\(W\times H\times C\)的特征图reshape成\(WH\times C\)的特征矩阵\(X\).
协方差矩阵的计算方式为\(\sum = X\bar{I} X^T\), \(\bar{I}=\frac{1}{s}(\mathbf{I}-\frac{1}{s}\mathbf{1})\) ,\(\mathbf{I, 1}\)分别是\(s\times s\)的identity矩阵和全1矩阵。之后进行特征值分解,在进行规范化(和MPN-COV一致,\(\alpha\)也是0.5)
得到的\(\hat{Y}=\sum^\alpha\)表示了通道层面特征的关联性。
\(z_c=H_{GCP}(y_c)=\frac{1}{C}\displaystyle\sum_i^Cy_c(i)\), \(H_{GCP}(\cdot)\)是global variance pooling,之后再利用gating
\(w=f(W_U\sigma(W_Dz))\), \(f(\cdot),\sigma(\cdot)\)分别是sigmoid和ReLU函数。
这个过程依赖于特征值分解,GPU不支持,采用基于Newton-Schulz迭代提出了快速矩阵规范化的方法。
MPN-COV【ICCV17】Is Second-order Information Helpful for Large-scale Visual Recognition?
之所以取幂,是为了解决在协方差估计中小样本高维度的问题,以resnet为例,最后得到的feature为7X7X512,也就是49个512维的feature,这样估计出来的协方差矩阵是不靠谱的,而通过幂这个操作,可以解决这一问题。通过实验可以发现,当幂次为0.5也就是平方根操作时,效果最优。
但是以上方法最大的问题在于计算矩阵的幂需要首先对协方差矩阵求特征值,而特征值操作在GPU上支持的非常不友好,这也就降低了该方法的效率。这也就衍生出下一篇文章,通过迭代的方式求取平方根,进而加速该方法。iSQRT-COV
实验结果
HAN【ECCV20】

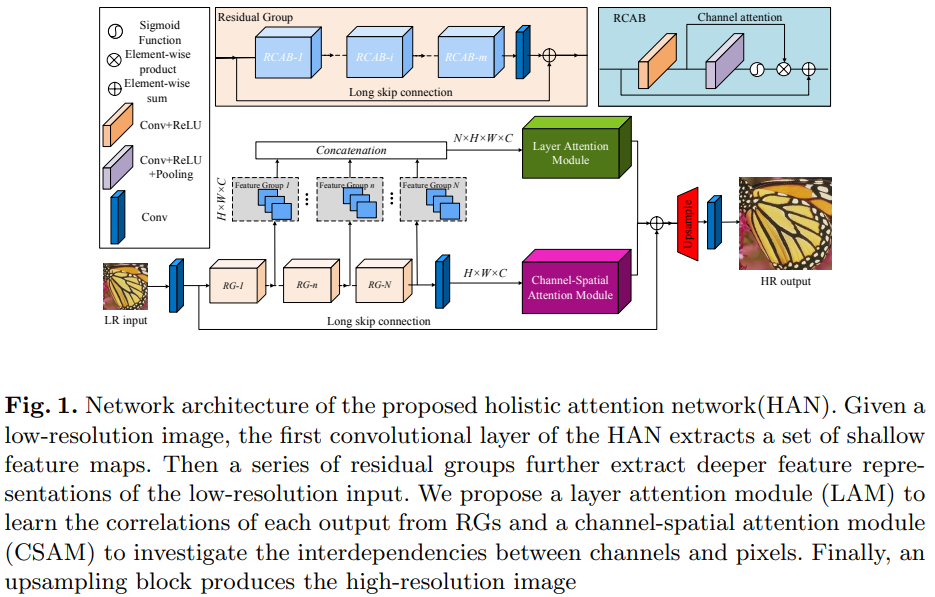
包含特征提取,层注意力,channel-spatial attention模块和重建模块四个部分。
特征提取部分,浅层特征由一层卷积进行提取,中间层特征使用RCAN作为backbone,每一个residual group都产生一个中间结果。
Holistic Attention,得到中间特征后,进行holistic feature weighting。包括对结构化特征进行的层注意力,取每一个residual groups的结果\(F_i\), \(F_L=H_{LA}(concatenate(F_1,F_2, ..., F_N))\)。以及对RCAN最后一层进行的channel-spatial的注意力, \(F_{CS}=H_{CSA}(F_N)\) 。虽然可以对每一个\(F_i\)都进行CSA,但是出于效率考虑指取最后一层。
图像重建,将\(F_L\)和\(F_{CS}\)进行element-wise求和,使用sub-pixel作为最后的upscale模块。引入长跳连接来稳定训练。因此sub-pixel的输入为\(F_0+F_L+F_{CS}\)
Layer Attention Module
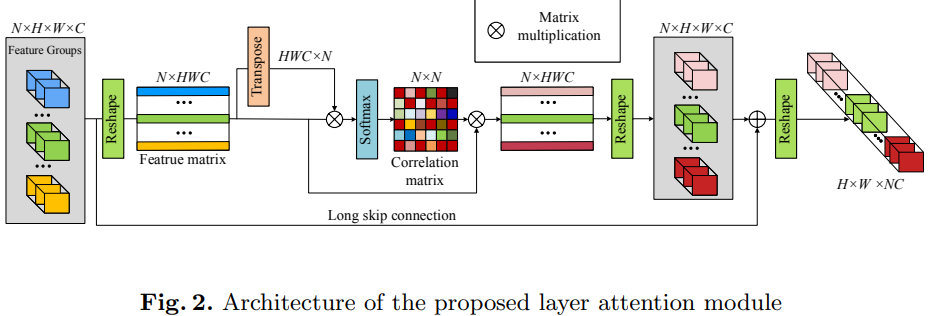
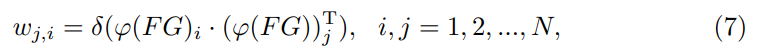
其中\(\sigma(\cdot),\varphi(\cdot)\)分别是softmax和reshape函数。\(F_{L_j}=\alpha\displaystyle\sum_{i=1}^Nw_{i,j}FG_i+FG_j\),\(\alpha\)初始化为0,在训练过程中逐步更新。
Channel-Spatial Attention
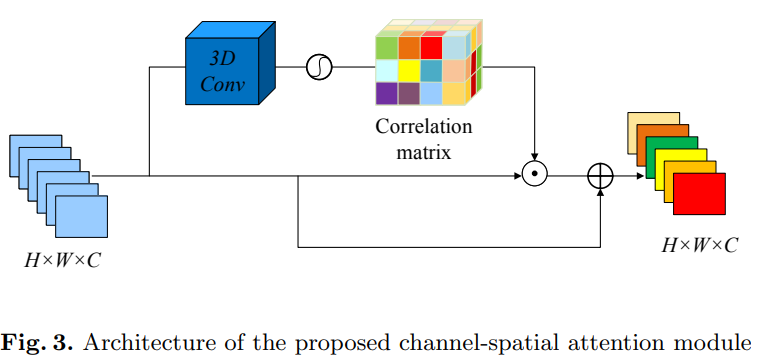
输入RCAN最后一层特征图\(F_N\in R^{H\times W\times C}\),进行3D卷积。文中使用\(3\times3\times3\)卷积,得到3组channel-spatial attention maps,\(W_{csa}\)
其中\(\sigma(\cdot),\bigodot\)分别是sigmoid和element-wist product函数。\(\beta\)也是初始化为0,在训练中逐步更新。
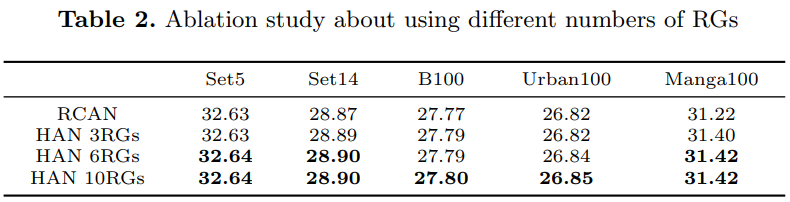
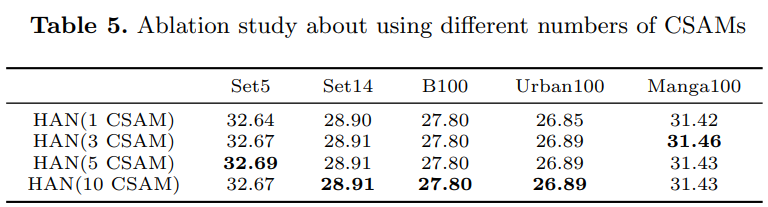
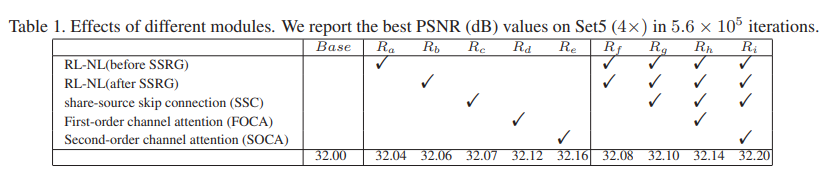
实验结果
各个模块的效果: