Deep Unfolding Network for Image Super-Resolution【USRNet】【阅读笔记】

　　CVPR20的文章，感觉想法挺棒的。

 

　　超分问题可以定义为$y=(x\otimes k)\downarrow_s+n$.他通常有两大类解决方法，早期通常是使用model-based方法。基于一些模型，比如MAP（最大后验概率）进行计算。在MAP的框架下，超分辨率重建是一个基于马尔科夫随机场先验模型的统计推断问题，即在给定低分辨率图像序列的条件下，通过选取与设计合理的马尔科夫随机场先验模型，使得超分辨率重建估计的高分辨率图像的后验概率达到最大。model-based方法不需要训练，可以适应不同的缩放因子s、模糊核k和噪声n，且具有比较好的可解释性。但是他的问题在于计算很复杂，从而限制了model-based方法的发展。在深度学习出现后，自然而然出现了将深度学习应用于超分问题的方法。但这种learning-based的方法灵活性较差，虽然目前已经可以在一个模型中处理不同缩放因子或是可以针对不同模糊核的方法，但是同时针对不同缩放因子、模糊核和噪声的工作较少。

　　本文的工作就是提出了一种方法结合model-based和learning-based，使得USRNet具有在一个模型中处理不同模糊核、缩放比和噪声的灵活性，又可以像learning-based方法一样以一种端到端的方式进行训练从而保证有效性和效率。本文工作的前提是模糊核和噪声是已知的。

 

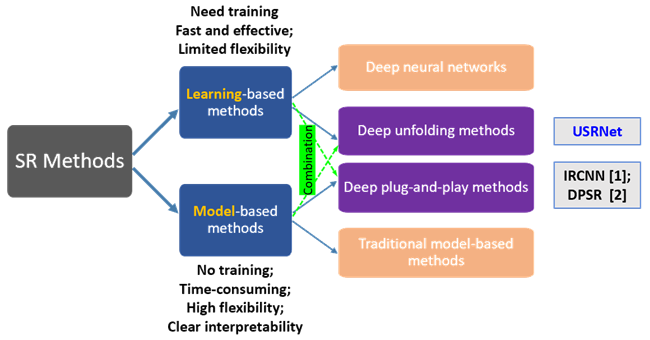
 　　目前实际上也有结合这两种方法的工作，即deep plug-and-play方法。但他是将学到的CNN作为先验plug进MAP框架中，因此他具有model-based方法的缺点。

　　而本文提出的方法作者称为是deep unfolding方法，核心是用半二次分裂法将问题分解为两个子问题。变量分裂法是解决目标函数是两个函数之和的优化问题。其中半二次分裂法一般是将正则项中的原始变量进行变量替换，然后增加拉格朗日乘子项和二次惩罚项，这么做的目的是，去耦合的同时，简化计算。对于超分问题目标就是要最小化$E(x)=\frac{1}{2\sigma^2}||y-(x\otimes k)\downarrow_s||^2+\lambda\Phi(x)$，其中$\lambda\Phi(x)$就是惩罚项或者叫prior term。再将惩罚项中的$x$替换为辅助变量$z$，$E_\mu(x, z)=\frac{1}{2\sigma^2}||y-(x\otimes k)\downarrow_s||^2+\lambda\Phi(x)+\frac{\mu}{2}||z-x||^2$，其中$\mu$为惩罚参数。

　　$z_k=argmin_z||y-(z\otimes k)\downarrow||^2+\mu\sigma^2||z-x_{k-1}||^2, x_k=argmin_x\frac{\mu}{2}||z_k-x||^2+\lambda\Phi(x)$。$z_k$可以用快速傅里叶变换计算得到（具体为什么不太明白...），对于$x_k$从贝叶斯角度来看他实际对应于一个噪声为$\beta_k$的去噪问题。

　　下图是作者提出的网络模型结构，包含三个模块：data module D用于计算$z_k$， prior module P用于计算$x_k$，计算时由于需要用到超参所以还引入了一个hyper-parameter module H用于计算每一次迭代时需要用到的$\alpha_k, \beta_k$，其中$\alpha_k$由$\sigma, \mu_k$决定，$\beta_k$由$\lambda, \mu_k$决定。作者指出，虽然可以去学到固定的$\lambda$和$\mu_k$，但让$\lambda, \mu_k$在迭代过程中随$\sigma, s$变化就足够了。

 

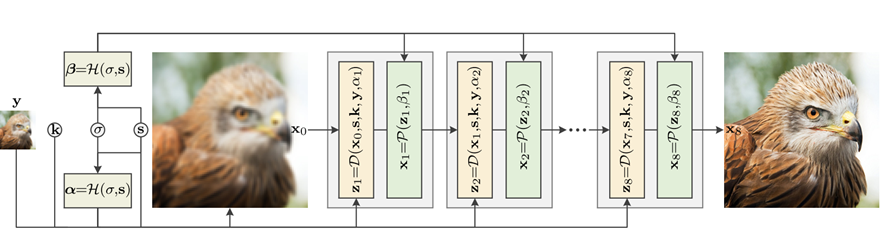
　　data module不包含任何可学习参数，并且将输入$y$与$s$进行最近邻插值得到$x_0$。P模块的结构为一个ResUNet，相当于一个denoiser，对$z_k$进行去噪得到cleaner的HR$x_k$。H的作用类似一个滑动条，$\alpha_k$增大会使$z_k$更接近于$x_{k-1}$，由3层全连接层组成。作者还指出，虽然这是针对SISR问题提出的，但是如果将缩放因子s设置为1，也可以将其应用于deblurring。

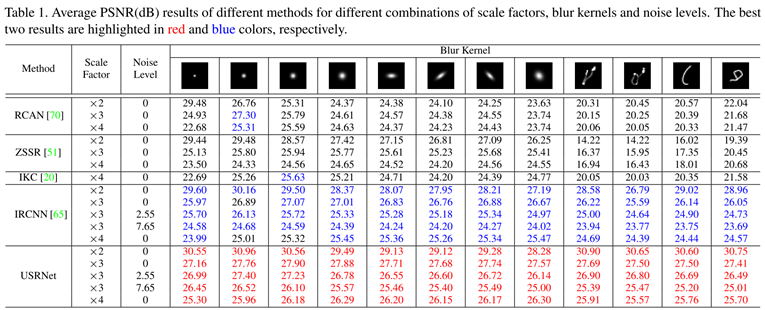
　　一些实验结果，感觉表现还是很好的。