How Does Batch Normalization Help Optimization?【阅读笔记】
NIPS2018的一篇文章，探究Batch Normalization起作用的背后原因。作者的结论是BN对缓解ICS问题作用非常微弱，BN的作用在于使得优化过程的landscape更光滑，其他的一些归一化方法也可以达到这样的效果。
Batch Normalization通过增加额外的层，控制层输入的均值和方差从而稳定了他的分布，使得神经网络的训练过程得到进步。尽管BN层的效果非常好，但是人们对于他有效的原因还不是非常理解。提出BN的原文的motivation是认为BN可以解决Interval Covariate Shift问题，从而帮助训练。但似乎很少有非常直接的证明，并且ICS问题和训练表现之间的关系也并不明确。
这篇文章的作者再CIFAR-10上训练了带BN和不带BN的两个VGG网络，使用BN的VGG在optimization和generalization方面都有很大的提升，但是通过visualize随机输入在训练过程的分布作者发现distributional stability(change in the mean and variance)非常微不足道。进而他提出了两个问题：
- BatchNorm的有效性是与ICS有关的吗？
- BatchNorm对每层输入分布的稳定是否有助于减小ICS问题？
第一个实验，作者在训练时在BatchNorm层之后插入随时间改变随机噪声，这个噪声是从一个non-zero mean，non-unit variance分布中采样得到的。这些噪声会提供非常严重的covariate shift。比较noisyBatchNorm、BatchNorm和standard三个网络的结果，发现noisyBatchNorm的结果和BatchNorm的非常接近，比standard的要好很多。而noisyBatchNorm每层的分布要比Standard的不稳定很多。这个实验解答了第一个问题，BatchNorm的有效性与ICS问题并不相关，至少在认为ICS是输入分布均值和方差的稳定性问题的时候是不相关的。
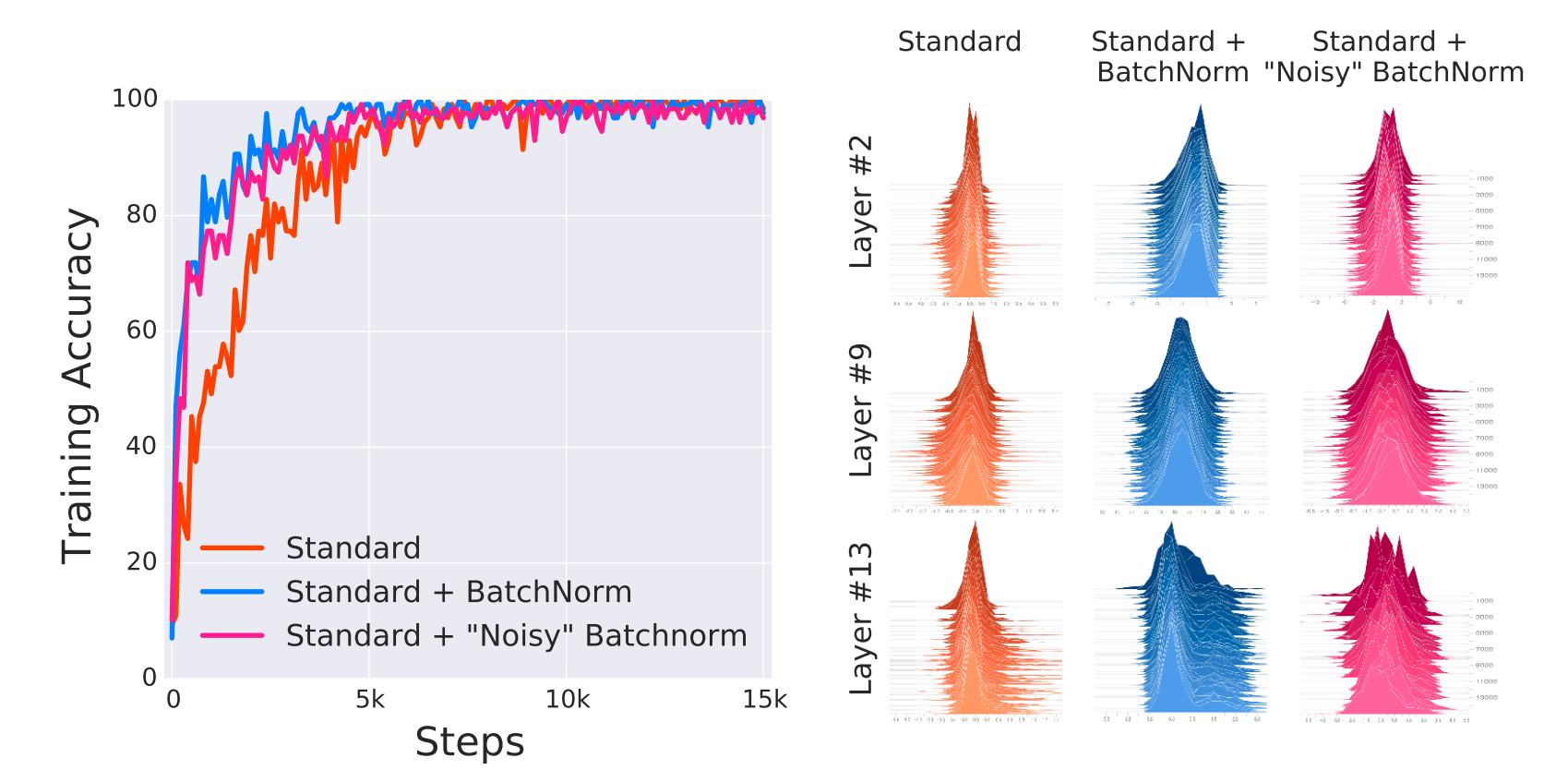
文中用一个更大的概念来考虑ICS问题，把第i个activation在t时间的ICS定义为参数更新前后更新后的梯度的欧式距离$||G_{t, i}-G'_{t,i}||_2$,其中
$G_{t,i}=\nabla_{W_i^{(t)}}\mathcal{L}(W_1^{(t)}, .., W_k^{(t)};x^{(t)}, y^{(t)}),G'_{t,i}=\nabla_{W_i^{(t)}}\mathcal{L}(W_1^{(t+1)}, ...,W_{i-1}^{(t+1)}, W_i^{(t)}, W_{i+1}^{(t)}, ..., W_k^{(t)};x^{(t)}, y^{(t)})$
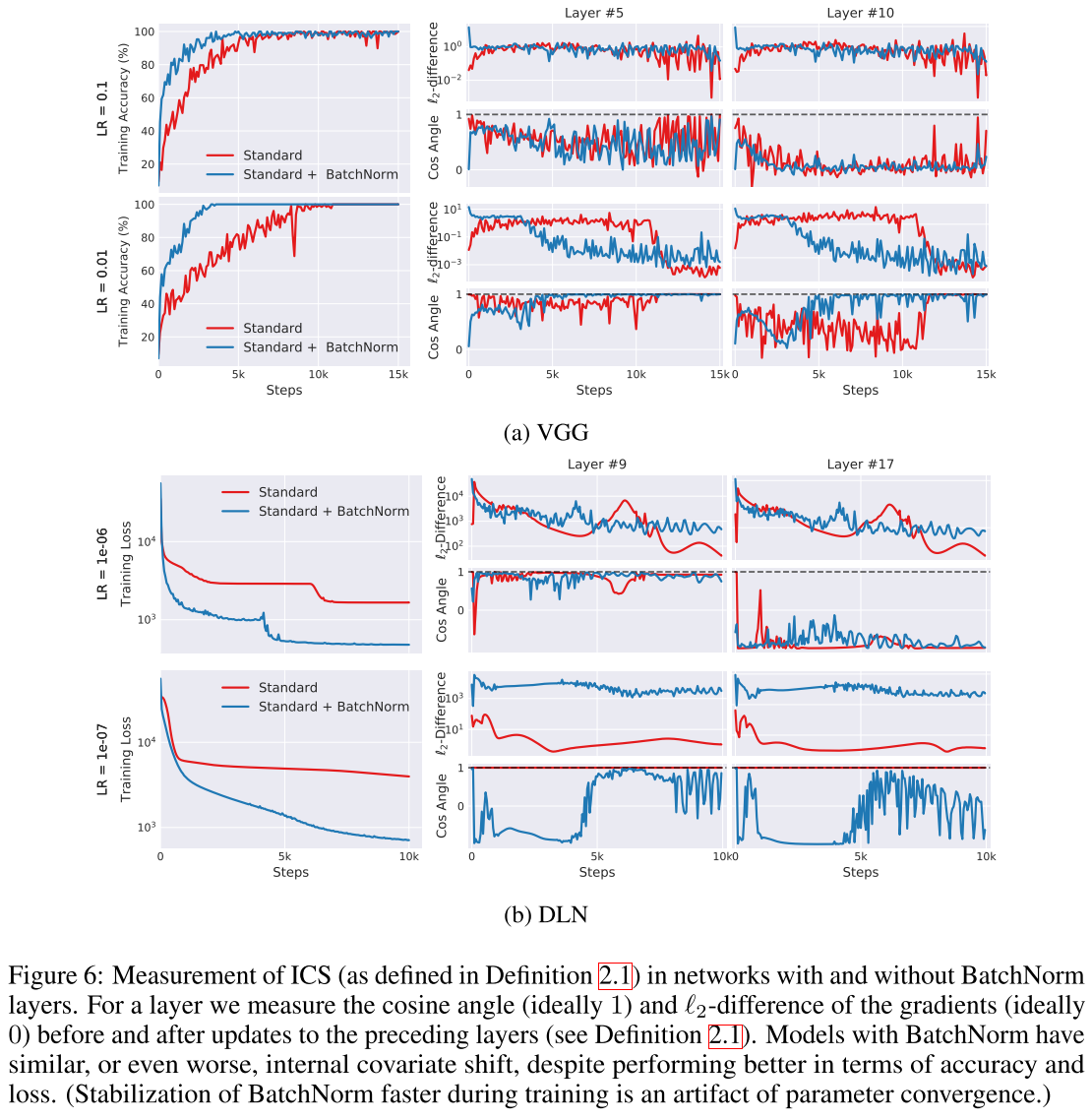
为了避免非线性函数的影响，实验在25层的线性模型上进行。使用full-batch gradient descent，避免随机性的影响。如果BatchNorm可以减小ICS，那么有BatchNorm层的网络$G$和$G‘$的相关性会增加。DLN中应该是几乎没有ICS的，但可以看到有BN层ICS反而增加了，尽管有BN层的准确率和Loss都要更好。这回答了作者的第二个问题，结论是从optimization的角度来看BatchNorm是没有减小ICS的。
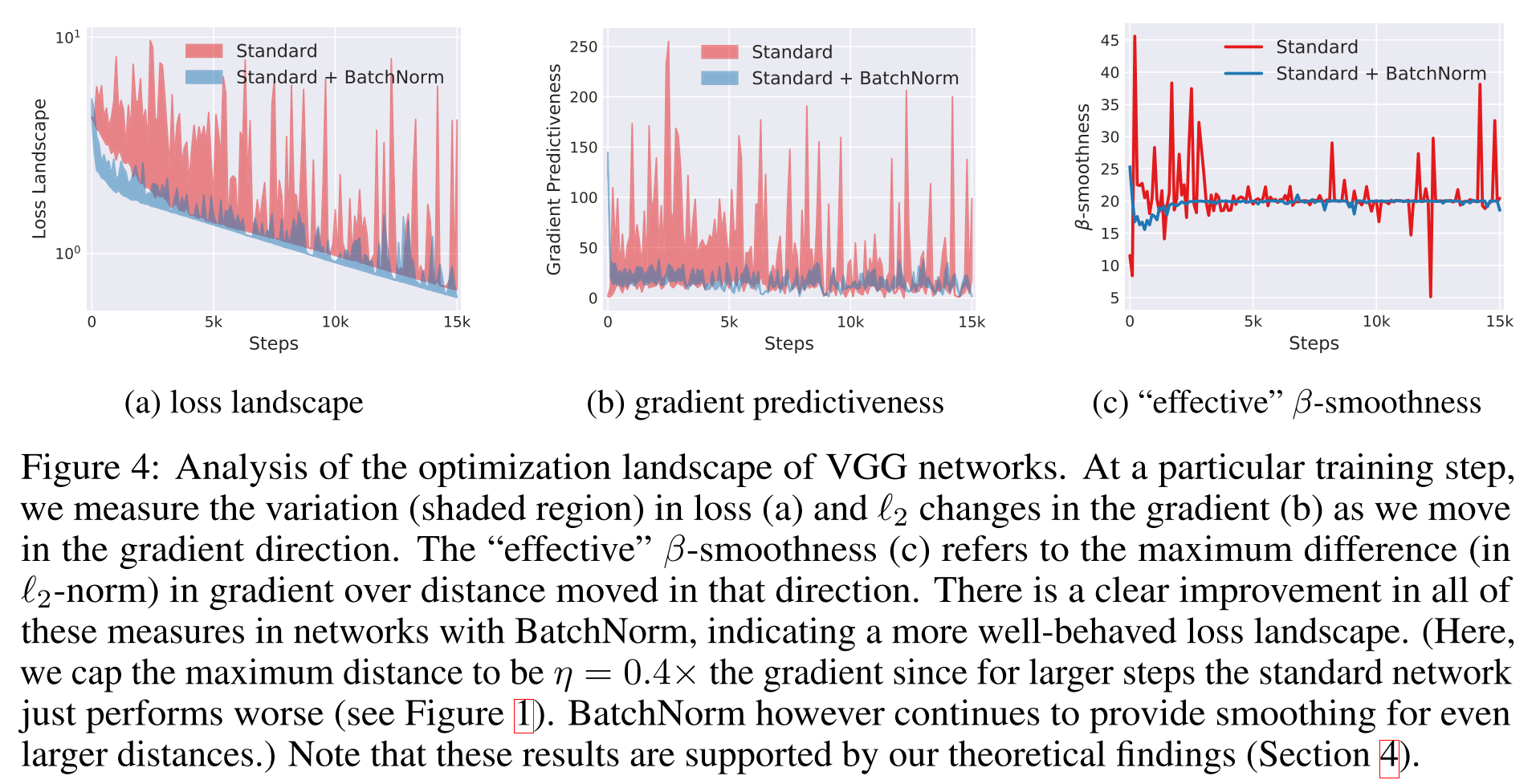
那么BatchNorm有效的原因究竟在哪里呢？作者认为关键在于reparametrizes the underlying optimization problem，使得优化问题的landscape显著地光滑了。原本loss function可能存在非常多的flat region或是sharp minima等。BatchNorm带来的光滑，使得gradients更加可靠且可预测。当我们沿着选定的梯度前进一大步时，更好的Lipschitzness说明这个梯度方向与实际梯度方向接近的概率更高，且不容易进入梯度消失/爆炸的区域。因此就可以选择更大范围的lr，对超参的选择也没有那么敏感。这里提到的Lipschitzness是函数光滑性的一个度量，是比通常连续更强的光滑条件。一个函数满足L-Lipschitz当且仅当对于所有的$x_1, x_2$，有$|f(x_1)-f(x_2)|\leqslant L||x_1-x_2||$。一个loss的Lipschitzness有所提升表明loss改变的速度更慢，gradient也更小。下面这张图是作者探究loss沿梯度方向的变化，但其他随机的方向也存在相似的表现。
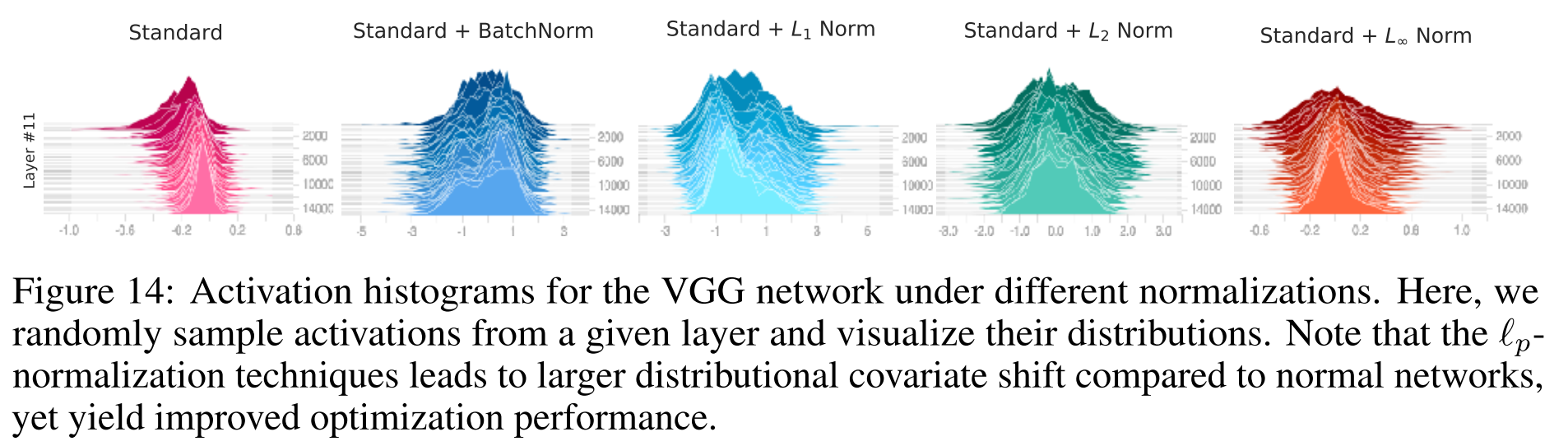
进而作者继续提问，BatchNorm是平滑landscape最好（唯一？）的方法吗？文中作者使用了$L_p norm, p=1, 2, \infty$进行归一化，这样得到的结果不是高斯分布，也不会保证分布的稳定性，ICS问题更加严重，但表现同样很好。作者的结论是BatchNorm对训练的积极作用是somewhat serendipitous（侥幸的，偶然的）。
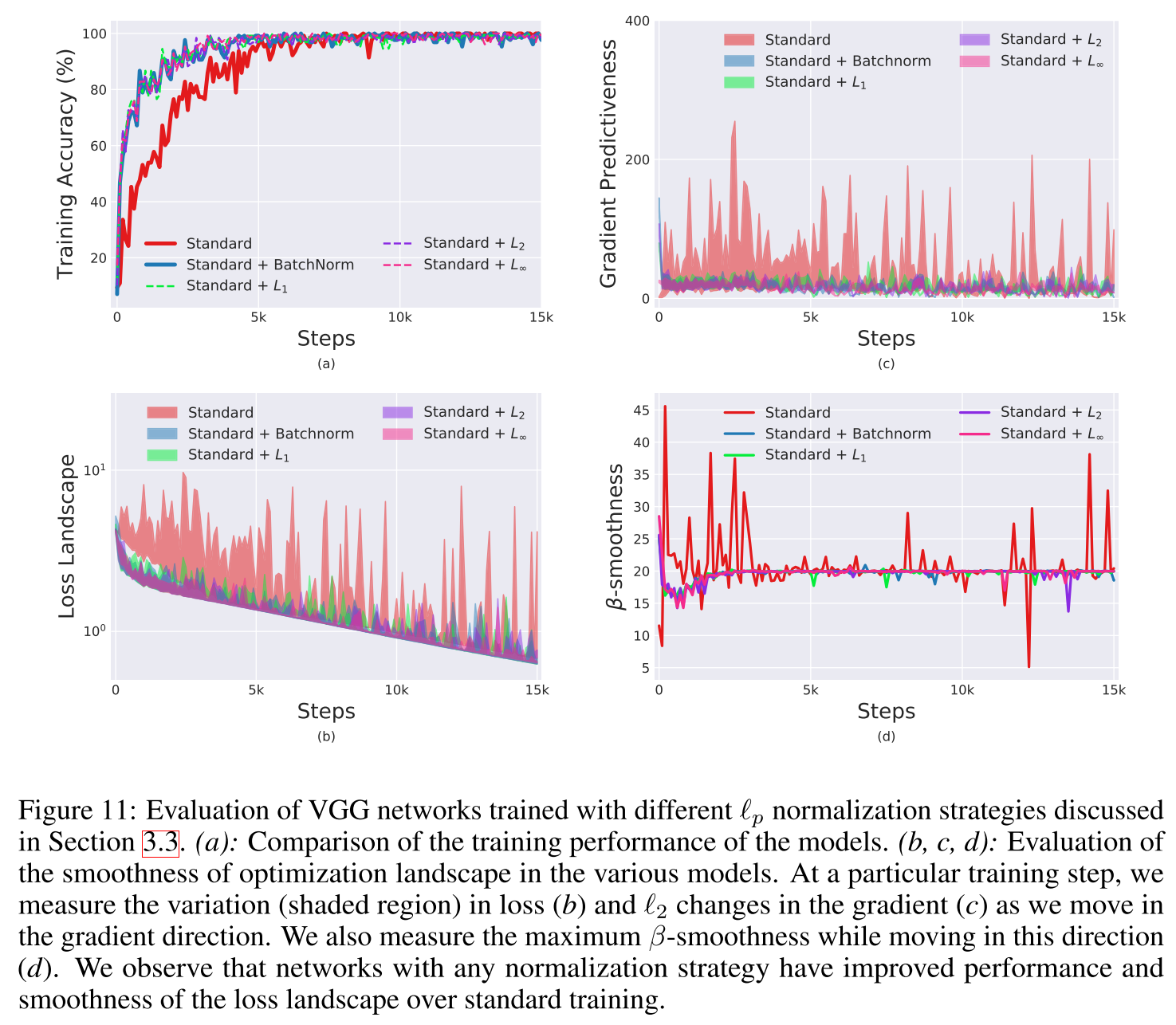
文中还有一大部分用数学公式从理论角度证明了上面的结论，没咋仔细看....
参考：https://zhuanlan.zhihu.com/p/52132614
