Squeeze-and-Excitation Networks【SENet】【阅读笔记】

提出了利用channel信息的SE(squeeze and excitation)模块，可以很大程度地提升表现而增加极少的计算消耗。

 

SE block

 

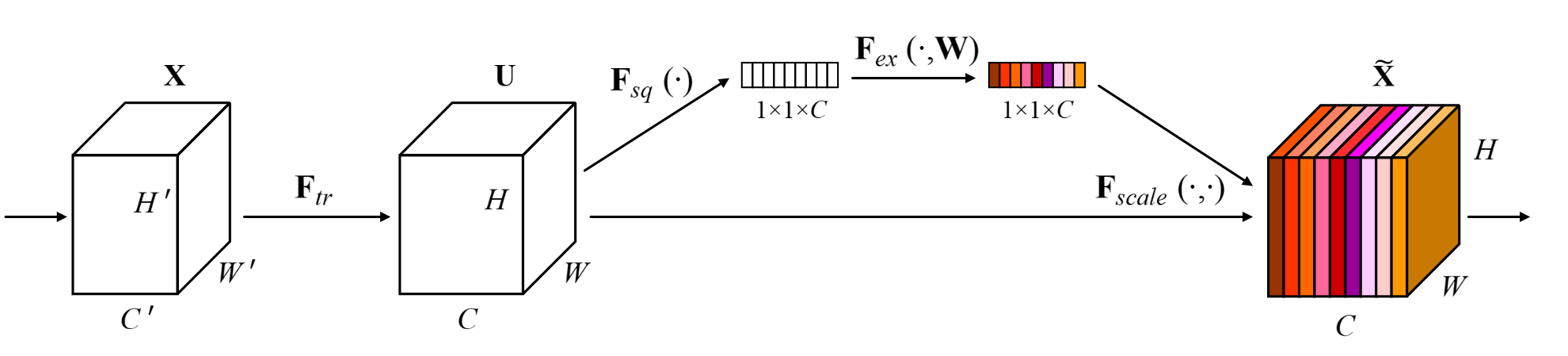
　　输入$X$经过了卷积操作$F_{tr}$后得到了特征图$U$。$u_c=v_c*X=\sum_{s=1}^{C'}v_c^s*x^s$，特征图中的值是所有C'的和。因此原来图像channel之间的依赖关系被隐式的嵌入到了卷积核$v_c$中。但这个信息受到了filter所捕捉的local spatial correlation的干扰。因此卷积操作捕捉到的channel关系是隐式且局部的。

　　SE block的目的是提供全局信息，帮助校准filter response，包含squeeze和excitation两个操作。特征图$U$首先经过squeeze操作，across their spatial dimensions 聚合特征图，产生一个针对channel的描述子。这个描述子的作用是产生一个关于channel级的feature response的全局分布的嵌入，使得网络全局感受野的信息可以被所有层使用。之后进行excitation操作，形式同一个简单的self-gating机制。将之前的嵌入作为输入，产生一个per-channel modulation weights的集合。这些weights会被用于和特征图$U$产生SE块的输出。

　　文中的squeeze操作使用的是global average pooling，$z_c=F_{sq}(u_c)=\frac{1}{H\times W}\sum_{i=1}^{H}\sum_{j=1}^{W}u_c(i,j)$。并且实验比较了averge要好于global max pooling，说明SE的表现对于特定aggregation的选择表现出较好的鲁棒性。由于他已经达到了比较好的效果因此没有考虑更复杂的操作。

　　excitation操作需要满足两个条件：一，灵活，可以学习channel间的非线性关系；二，学习到的是一个非互斥的关系，确保多个channel可以被激活。文中使用的是sigmoid函数。$s=F_ex(u_c)=\sigma(g(z, W))=\sigma(W_2\delta(W_1, z))$， $\delta$为ReLU函数，$W_1\in \mathbb{R}^{\frac{c}{r}\times c}, W_2\in\mathbb{R}^{c\times \frac{c}{r}}$为了限制模型的复杂性，辅助模型更好地generalize，引入了两层bottleneck型的FC层。文中实验比较了sigmoid，tanh，ReLU函数，三种函数的效果sigmoid>tanh>ReLU.并且，ReLU甚至会造成表现比baseline差的现象，说明excitation操作的选择对于SE block非常重要。

　　一个完整的SE模块如下图：

 

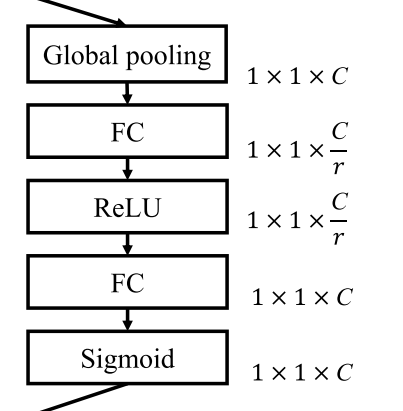
　　excitation中存在一个参数reduction ratio$r$，针对$r$的选择文中进行了实验，$r$增大会导致网络参数量减少，而error会先减小后增大。实验发现$r=16$时准确率和模型复杂性的平衡较好。并且文中指出，在整个网络中使用同一个$r$不一定是最优的，可以针对不同层尝试不同的$r$。

　　作者还探究了SE块在网络不同层的作用，结果表明他在每一层都能起到作用，而且每一层的作用是互补的。此外，对于SE与网络的卷积模块的结构也进行了实验。比较了一下四种结构。实验表明SE-PRE,SE-Identity和Standard的表现比较接近，SE-POST表现不好。还尝试了将SE直接置于残差单元中$3\times3$的卷积之后，其表现也和标准的结构很接近，并且由于$3\times3$卷积设计的channel较少，其参数量也较少。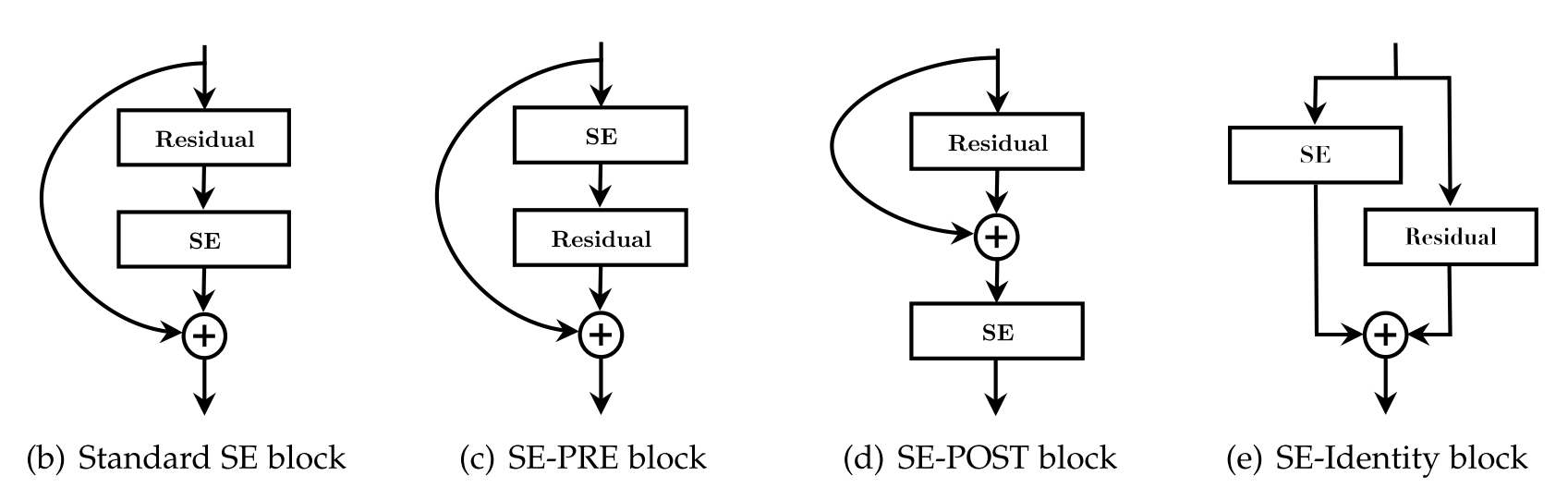

 

　　作者在文中以ResNet50为基础对原始网络和加入SE模块后的网络的计算速度和参数量进行了比较。当$r=16$时，SE-ResNet50的时延增加不大，参数量增加约10%，但效果明显提升。这部分参数量大部分是源于网络最后一个阶段的excitation操作，由于此时channel数较多。通过画出不同类别的activation证明，在网络的最后阶段可以适当去除SE模块，对表现的影响很小但参数量的增加可以减少到4%。

　　作者将SE模块应用于很多主干模型，其表现均有所提升。并且在ImageNet, CIFAR10, CIFAR100验证了分类效果，在Places365-Challenge中验证了场景分类效果，COCO中验证了目标检测效果。