洛谷P1169 棋盘制作【悬线法】【区间dp】

题目：https://www.luogu.org/problemnew/show/P1169

题意：n*m的黑白格子，找到面积最大的黑白相间的正方形和矩形。

思路：传说中的悬线法！用下面这张图说明一下。

悬线法一般是用来求一个没有障碍点的最大子矩阵的。想象从上面垂下来好多的悬线，这些悬线被一个底所限制，并且可以左右移动但是也有范围限制。

现在某条悬线可以移动到的面积就是他能满足的子矩形的面积。比如我们已经处理好了$i-1$行，现在考虑$(i,j)$

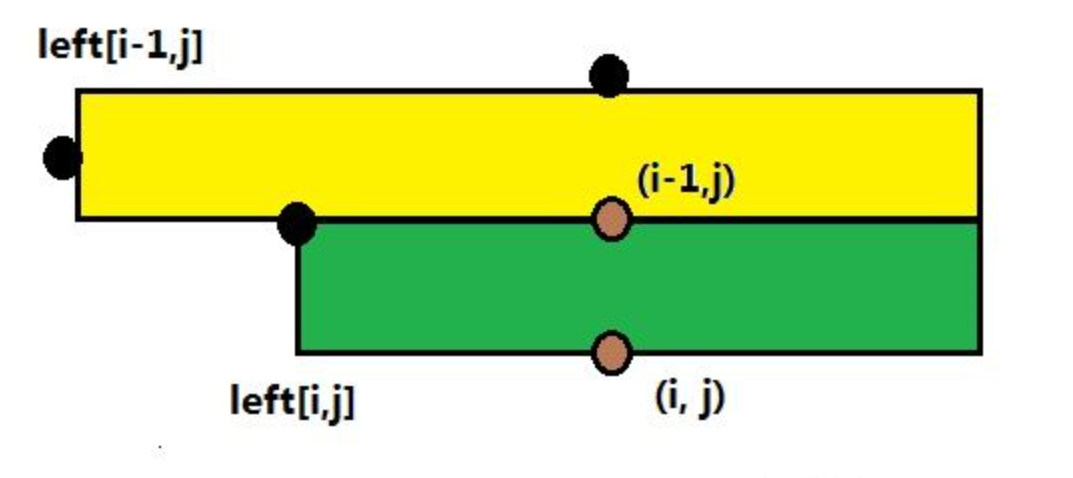
对于这道题来说，如果$grid[i][j]!=grid[i-1][j]$就说明他们黑白颜色不同，那么这个以$i$行为底的悬线的高度就是$height[i-1][j]+1$

接下来我们考虑他的左右范围

首先我们可以需要预处理出每个位置可以到的左右范围，比如说$lft[i][j]$就是从$(i,j)$开始往左满足左右相间可以一直到第几列。

当我们要扩展一行的时候对于左边界只能取最右边的一个，对于右边界只能取最左边的。

#include<cstdio>
#include<cstdlib>
#include<map>
#include<set>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath> 
#include<stack>
#include<queue>
#include<iostream>

#define inf 0x3f3f3f3f
using namespace std;
typedef long long LL;
typedef pair<int, int> pr;

int n, m;
const int maxn = 2005; 
int grid[maxn][maxn];
int lft[maxn][maxn], rgt[maxn][maxn], height[maxn][maxn];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            scanf("%d", &grid[i][j]);
            lft[i][j] = rgt[i][j] = j;
            height[i][j] = 1;
        }
    }
    
    for(int i = 1; i <= n; i++){
        for(int j = 2; j <= m; j++){
            if(grid[i][j] != grid[i][j - 1]){
                lft[i][j] = lft[i][j - 1];
            }
        }
        for(int j = m - 1; j > 0; j--){
            if(grid[i][j] != grid[i][j + 1]){
                rgt[i][j] = rgt[i][j + 1];
            }
        }
    }
    
    int anssqu = 0, ansrec = 0;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            if(i > 1 && grid[i][j] != grid[i - 1][j]){
                lft[i][j] = max(lft[i][j], lft[i - 1][j]);
                rgt[i][j] = min(rgt[i][j], rgt[i - 1][j]);
                height[i][j] = height[i - 1][j] + 1;
            }
            int row = rgt[i][j] - lft[i][j] + 1;
            int col = min(row, height[i][j]);
            anssqu = max(anssqu, col * col);
            ansrec = max(ansrec, row * height[i][j]);
        }
    }
    
    printf("%d\n%d\n", anssqu, ansrec);
}