经典结构 窗口最大值更新结构

内容：

1、窗口内最大值更新结构

2、窗口移动

3、求达标的子数组个数

 

 

 

1、窗口内最大值更新结构

窗口：数组中的一系列数

• L与R之间的数就是窗口内的数 
• L和R的初始位置为数组的左边，可表示为-1
• L和R都只能右移，不可后退；且L不可超过R

窗口内最大值更新结构实质上就是一个双端队列(双向链表实现)，可以从头部放入数据、弹出数据，也可以从尾部放入数据、弹出数据(均是O(1))

双端队列中每个元素由value和index组成，value是值，index是时间戳(数组下标)

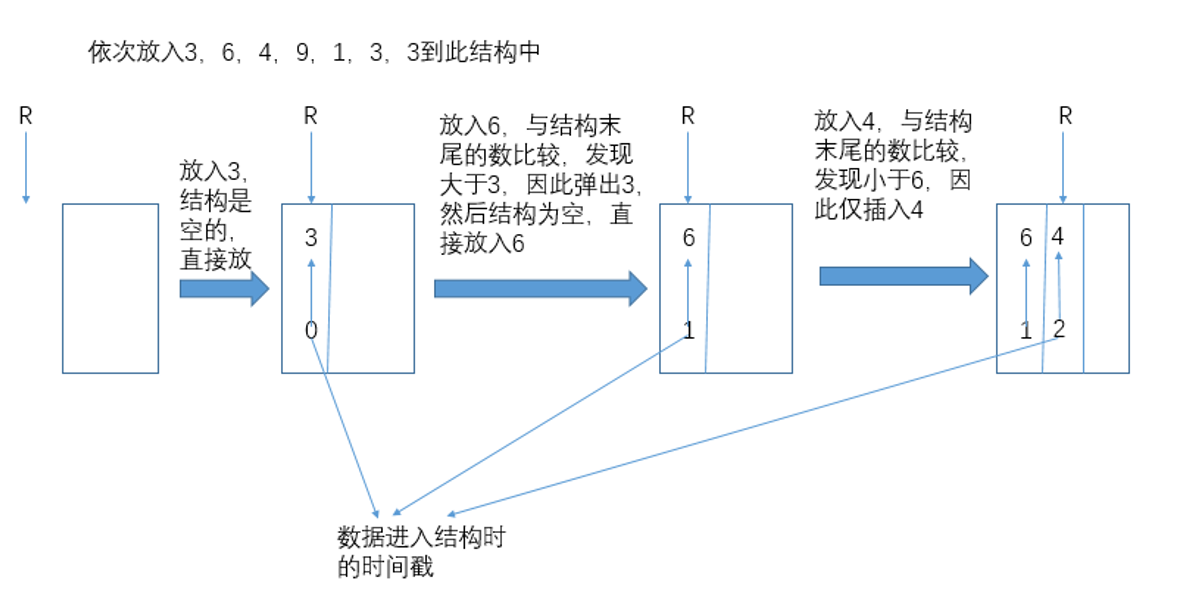
双向队列加数策略：R右移，则向双向队列中加数；如果尾部元素比要加入的数小，则弹出尾部的数，一直弹，

直到尾部的数大于新加入的数，或者队列为空。

解释：如果新加入的数据，比之前的数大，那么之前的数就不可能是窗口内最大值，可以舍弃掉。

双向队列减数策略: L右移，则需要处理，如果刚被移出窗口的数是队列头部的数则把队列头部的数弹出，这就是为什么要保存数组下标的原因

窗口内最小值类似：双向队列从头到尾依次递增，加数如果尾部数比要加的数大则弹出，减数也是过期就弹出；

代码：

// 最大值窗口更新结构
public class MaxValueWindow {
    
    private LinkedList<Integer> queue;
    public MaxValueWindow(){
        this.queue = new LinkedList<Integer>();
    }
    
    // 更新窗口最大值
    public void add(int i){
        while(!queue.isEmpty() && queue.getLast() <= i){
            queue.pollLast();    
        }
        queue.addLast(i);        
    }
    
    // 获取窗口最大值
    public int getMax(){
        if(!queue.isEmpty()){
            return queue.peekFirst();    
        }
        return Integer.MIN_VALUE;
    }
    
    // 使窗口最大值过期
    public void expireMaxValue(){
        if(!queue.isEmpty()){
            queue.pollFirst();
        }
    }
    
    public static void main(String[] args) {
        MaxValueWindow window = new MaxValueWindow();
        window.add(6);
        window.add(4);
        window.add(9);
        window.add(8);
        System.out.println(window.getMax());    // 9
        window.expireMaxValue();
        System.out.println(window.getMax());    // 8
    }
}

 

 

2、窗口移动

题目描述：

有一个整形数组arr和一个大小为w的窗口从数组的最左边滑到最右边，窗口每次向右滑动一个位置

例如：数组为[4，3，5，4，3，3，6，7]，窗口大小为3时：

[4 3 5] 4 3 3 6 7　　窗口中最大值为5

4 [3 5 4] 3 3 6 7　　窗口中最大值为5

4 3 [5 4 3] 3 6 7　　窗口中最大值为5

4 3 5 [4 3 3] 6 7　　窗口中最大值为4

4 3 5 4 [3 3 6] 7　　窗口中最大值为6

4 3 5 4 3 [3 6 7]　　窗口中最大值为7

如果数组长度为n 窗口大小为w 则一共产生n-w+1个窗口的最大值

请实现一个函数：

输入：整形数组arr  窗口大小w

输出：一个长度为n-w+1的数组res  res[i]表示每一种窗口状态下的最大值

以上面的数组为例，结果应该返回[5, 5, 5, 4, 6, 7]

 

思路：

前面介绍的窗口大值更新结构的特性是，先前放入的数如果还存在于结构中，那么该数一定比后放入的数都大。

此题窗口移动的过程就是从窗口中减一个数和增一个数的过程

 

代码：

public class SlidingWindowMaxArray {
    public static int[] getMaxWindow(int[] arr, int w) {
        if (arr == null || w < 1 || arr.length < w) {
            return null;
        }
        LinkedList<Integer> qmax = new LinkedList<Integer>();
        int[] res = new int[arr.length - w + 1];
        int index = 0;
        for (int i = 0; i < arr.length; i++) {
            while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[i]) {
                qmax.pollLast();
            }
            qmax.addLast(i);
            if (qmax.peekFirst() == i - w) {
                qmax.pollFirst();
            }
            if (i >= w - 1) {
                res[index++] = arr[qmax.peekFirst()];
            }
        }
        return res;
    }
    
    public static void main(String[] args) {
        int[] arr = {4, 3, 5, 4, 3, 3, 6, 7};
        System.out.println(Arrays.toString(getMaxWindow(arr, 3)));
    }
}

 

 

3、求达标的子数组个数

题目描述：求最大值减去最小值小于或等于num的子数组数量

给定数组arr和整数num，共返回有多少个子数组满足如下情况：

max(arr[i...j]) - min(arr[i..j])  <=  num

max(arr[i...j])表示子数组arr[i...j]中的最大值，min(arr[i...j])表示子数组arr[i...j]中的最小值

要求：实现时间复杂度O(N)的算法

 

暴力思路：

遍历每个元素，再遍历以当前元素为首的所有子数组，再遍历子数组找到其中的大值和小值以判断其是否达标。

很显然这种方法的时间复杂度为 o(N^3) ，但如果使用窗口最大值更新结构，则能实现 O(N) 级别的解

代码： 

    // 暴力方法(O(N^3))
    public static int getNum1(int[] arr, int num) {
        int res = 0;
        // 遍历所有子数组
        for (int start = 0; start < arr.length; start++) {
            for(int end=start;end<arr.length;end++){
                if(isValid(arr, start, end, num)){
                    res++;
                }
            }
        }
        return res;
    }
    
    public static boolean isValid(int[] arr, int start, int end, int num){
        // 判断子数组最大值和最小值是否小于num
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        for(int i=start; i<=end;i++){
            max = Math.max(max, arr[i]);
            min = Math.min(min, arr[i]);
        }
        return max - min <= num;
    }

 

窗口最大值更新结构思路：

基本思想：

• 前提条件：用 L 和 R 两个指针指向数组的两个下标，且 L 在 R 的左边，下面两条是必然发生的
• 当 L~R 这一子数组达标时，可以推导出以 L 开头的长度不超过 R-L+1 的所有子数组都达标
• 当 L~R 这一子数组不达标时，无论 L 向左扩多少个位置或者 R 向 右扩多少个位置， L~R 还是不达标

O(N) 的解对应的算法是：

L 和 R 都从0开始， R 先向右移动， R 每右移一个位置就使用窗口最大值更新结构和窗口最小值更新结构

记录一下 L~R 之间的大值和小值的下标，当 R 移动到如果再右移一个位置 L~R 就不达标了时停 止，这时以当前 L开头

的长度不超过 R-L+1 的子数组都达标；然后 L 右移一个位置，同时更新一下结构（ L-1 下标过期），

再右移 R 至 R 如果右移一个位置 L~R 就不达标了停止（每右移 R 一次也更新结构）……；直到

L 到达数组尾元素为止。将每次 R 停止时， R-L+1 的数量累加起来就是 O(N) 的解，因为 L 和 R 都只向右移动，

并且每次 R 停止时，以 L 开头的达标子串的数量直接通过 R-L+1 计算，所以 时间复杂度就是将数组遍历了一遍即 O(N)

代码：

    // O(N)的解法
    public static int getNum(int[] arr, int num) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        LinkedList<Integer> qmin = new LinkedList<Integer>();
        LinkedList<Integer> qmax = new LinkedList<Integer>();
        int L = 0;
        int R = 0;
        int res = 0;
        while (L < arr.length) {
            while (R < arr.length) {
                // R往右扩 扩到不能扩停
                while (!qmin.isEmpty() && arr[qmin.peekLast()] >= arr[R]) {
                    qmin.pollLast();
                }
                qmin.addLast(R);
                while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[R]) {
                    qmax.pollLast();
                }
                qmax.addLast(R);
                if (arr[qmax.getFirst()] - arr[qmin.getFirst()] > num) {
                    // 不达标的情况
                    break;
                }
                R++;
            }
            // 更新最大最小值
            if (qmin.peekFirst() == L) {
                qmin.pollFirst();
            }
            if (qmax.peekFirst() == L) {
                qmax.pollFirst();
            }
            // 加上已统计的结果
            res += R - L + 1;
            // L右扩
            L++;
        }
        return res;
    }