2023 7 月总结

经典的，日期在当天的题可能并不是当天做的，这时为了分类的考虑。

总结绝大部分都是在 8 月份写的， 算是把每一个题都做了两遍了。

7.3

太久没碰 OI 了，感觉非常手生。

「CF1394D」Boboniu and Jianghu

solve by myself.

思维含量不大，但是讲究了一个简洁与否的问题，但是我做得很不好，特别反应了树形 DP 练度不够，不熟悉，甚至害怕的老问题的延续。

一眼树形 DP，f[i][0/1] 表示 i 子树处理完了，边 (i,fa_i) 的方向如何。状态转移形如在根节点处的路径拼接，那么考虑经典的树形背包的转移模式，即考虑每次添加一棵子树。

写了一会儿发现这样做有本质上的问题，发现需要记录当前有多少条链没有合并，而不能仅仅记录有没有没有合并的链，那么这样复杂度就爆炸了，是不可以的。

这个时候回头看，发现自己第一眼的想法太 naive 了，做题太急躁了，还有性质没有发掘到。一个很显然的简化是，对于 \(b_u\neq b_v\)，边 \((u,v)\) 已经定向了。

那么只需要考虑 \(b_u == b_v\) 怎么办，容易想到把这种儿子提出来，枚举定向 \(<u,v>\) 的数量，计算花费并取最小值。

思路是正确的，但是问题是计算花费的方式太愚蠢了，设 in 表示入边数量, out 表示出边，我的方法是先假装不存在链的拼接所带来的 a[u] 的减少，最后减去 a[u] * min(in, out)，写得巨丑。

实际上，上述操作已然将 \(\sum 链贡献 = \sum 点贡献\)，但是却还是按照 链和 的思路进行状态转移，u 的实际贡献其实就是 \(a[u] \times \max(in, out)\)，这样实现会简明很多。

「LOJ6669」 Nauuo and Binary Tree

solve by solution.

最开始看错题了，不知道是二叉树，完全不会做。

有趣的交互题，考察对分治和树链剖分的理解。

容易想到先问出深度，这是比较有用且容易得到的信息。考虑暴力怎么做，因为只有深度信息，考虑按照深度从小到大确定每一个点，设已经确定 x 在节点 u 的子树内，那么只需要问一下 x 和 u 的儿子即可。这样总询问次数是 \sum dep，万万不可。

发现现在的问题是“查询操作”太慢，查询方式非常丑陋，那么这变成一个优化结构问题了，需要一种合适的组织信息的方式。这种组织信息的方式要保证原树的形态，所以点分治之类的技巧是行不通的；同时这种组织方式还要求适应题目所给的询问方式，发现树链剖分是一个很好的结构，我们可以只走轻边来保证复杂度。

也就是说，假设已经确定 x 在节点 u 的子树内，已知 u 到叶子的一条重链，现在想要找到 x 是从重链上哪一个点走轻边。问一问 x 和当前重链底部的 lca 就好了。

（这个原理可以联想到树剖求 lca）

每次新确定一个点，可以暴力重做树剖。假如时间复杂度不允许，可以上 LCT。

「UOJ618」聚会2

solve half

容易发现聚会点的定义就是中位数的定义。

显然奇数情况中位数只有一个，偶数的话，可能的聚会点是两个中位数之间的链。

对于有 x 只河狸，x 是偶数，现在的问题等价于问 \(\max_{i, j} dis(i, j)\)，使得 \(siz[i] >= x / 2 \wedge siz[j] >= x / 2\)。当时想到这里就没有想下去了，以为后面的处理是简单的。

其实并不简单。

一个重要的细节是这个 siz[i] 的取法，应该取的是 n - 以 i 为根时最大子树大小。也很容易理解，考虑最后作为答案的 i, j 就知道这样是优的。

知道 siz 后，按照 siz 从大到小加入集合，维护集合直径 即可，这里有一个倒序处理的小亮点。

[UOJ33] 树上GCD

随便推推狮子，知道需要求的是 F[k] 表示 (i, j) 的对数使得 \(k | d(i, a) \wedge k | d(j, a)\)，然后不会了。

solution：

树上路径问题，仍然考虑淀粉质，特殊在于此处是有根树。

考虑对于一个分治中心 G，对于 G 的子树，没啥特殊的，类似树形背包每次合并两个子树统计答案。处理数组 cnt[i] 表示深度为 i 的个数，处理 f[i] 表示深度为 i 的倍数的个数，每次合并子树，cnt 对应位相加，f 对应位相乘。

对于 G 的祖先的部分，对于祖先 y，处理出 y 不包含 G 的儿子的子树的 cnt 和 f，问题在于多了一点距离，做不了对应位相乘。

对 k 执行 根号分治，小于 \sqrt n 的部分，对 G 的子树预处理 \(modf[i][k]\) 表示距离 mod k = i 的点的数量，对于距离为 d 的祖先 y，每次 \(F[k] += f[i] \times modf[i - d][k]\)；大于 \sqrt n，暴力做。

「CF830E」 Perpetual Motion Machine

by solution：

大神笔题

发现贡献涉及到 \(xy\) 和 \(x^2 + y^2\) 的比较，想到假如让 \(\forall x, x^2 > 1/2\sum_e xy\) 就好了！

有这样一个不等式：

\[\begin{align} px^2 + qy^2 >= xy, pq = \frac 14, x >= y, p >= q \end{align} \]

那么，假如当前对于每一条边，都有了一个分配 (p, q) 的方案，每次 \(a[x] += p, a[y] += q\), 使得 \(\forall x, a[x] >= 1\) 就好了！

这是因为对于每一个 p, q，一定可以找出使得等号成立的解集，一步一步推下去，全局就有解。这个条件显然是充要的。

那么这样岂不是不存在无解？不是的，因为题目还要求了整数解，而且有值域范围的限制。

将这个结论运用到分析中：

1. 假如图存在环，那么环上点权值 1，其他点全是 0 即可。
2. 假如存在四度点，那么 1/4, 1/4, 1/4, 1/4, 1，对应解 2，2，2，2，1
3. 假如存在两个三度点且这两个点联通，那么这两个三度点可以“合并”成为一个四度点
4. 假如没有三度点，那么一定是链，那么 GG。
5. 假如存在 1 个三度点，经过 手摸/打表/高超的数学分析，可以知道有解当且仅当延申出去的三条链的长度 >= (2,2,2) 或 (1, 3, 3) 或 (1, 2, 5)

「CF1514E」 Baby Ehab's Hyper Apartment

solution：

竞赛图，考虑先求出一条哈密顿路！

使用经典二分，可以在 nlogn 的操作次数内得到。

剩下的问题在于求强连通块，从路末开始，假如存在向前的边，加边，加边，并查集！

「CF1535F」 String Distance

答案只能是 1/2/1337

1337 是容易的，两个字符串的各自的可重字符集不相同的对数。

对于 2，可以用总数减去 1 的个数，问题在于求 1 的个数。

1 的个数需要两个字符串 s, t 满足：

1. 可重字符集相同
2. s ^ t = [l, r]，即只有一个连续段不同
3. 对于 s， [l, r] 单调递增

还有一个隐约的问题是一个 s, t 可能会对应多个 [l, r]。

solution：

对于每一种字符集：枚举 s，枚举 极长上升连续段 [l, r]，需要计算的是 s ^ t \in [l, r]。

这样不会算重，因为是极长！！！！

字符串匹配问题，对于正反串建立 trie，问题变成二维数点

「CF1508D」Swap Pass

高明的构造！

solution：

对于一个置换环，只需要选取环上最左最下的点，依次交换即可。

存在多个置换环，任意交换两个置换环中的点，使得两个置换环合并即可。

为了使得合并时的交换不影响后续操作，应该极角排序之后顺次检查。

bugs:

1 i 写反，警钟敲烂。

「CF1603D」 Artistic Partition

solution：

容易写出 dp 式子，发现状态数巨多，此时应该怎么办！！

常见的思维可能是重新设计状态，包括交换答案和状态、组合意义等技巧，或者直接另辟蹊径。

这里给出另外一条路：\(\textcolor{red}{\rm{new!!!}}\) 考察有意义状态

我们猜测假如 k 比较大，那么答案显然不会很大。

具体的，发现 \(c(l, r) \geq r - l + 1, c(x, 2x - 1) = x\)，所以说，假如划分为 \([1,1], [2,3], [4,7]...\)，答案是最小值 n。

所以，只需要计算 \(O(log n)\) 级别的 k 就好。

直接转移是 \(O(n^2k)\)，容易猜测决策单调性，使用分治优化决策单调性，采用类似莫队的方式计算 c(l, r)，总复杂度 \(O(knlog n \times 指针移动复杂度)\)。

推一推式子，发现 \(c(l, r) = \sum_{x = l}^r sphi[r / x]\)，l 移动是简单的，对于 \(r - 1\to r\)，推一推式子发现 \(\delta = \sum_{x >= l \wedge x | r} phi[r / x]\)，考虑暴力枚举 r 的因子，由于 r 移动次数是 nlogn，摊下来复杂度就是 nlog^2n。

总复杂度 \(O(knlog^2n)\), \(k = O(\log n)\)

bugs： “莫队” 指针移动，写 while(l < ql) 的时候复制 while(l > ql)，+- 写反。

「ARC153E」 Deque Minimization

分析分析，发现一定是往头部塞了一个数之后，然后一坨数字塞到尾部，称这坨数字属于头部的那个。

考虑区间 DP，设 \(f_{l,r}\)，那么 \(l - 1\) 会拥有 \([r + 1, k]\)，但是没有必要枚举 k，转移可以写得优雅一点：

\(Y_{l−1} ≤ Y_l, f_{l,r}\to f_{l−1,r}\)

\(Y_l<Y_r, f_{l,r}\to f_{l,r+1}\)
​
这样是 \(O(n^2)\) 的。

观察到很多状态是多余的，设 \(a_{1\dots p}\) 是极长不增段，那么 \(l\le p\)

观察到对于 \(a_l\) 相同的段，第二种转移的形式一致，且实际上就是做 \(k\) 次前缀和之类的事情。

考虑倒序枚举 \(l\)，动态维护 $f_{l,r}。对于一个同色连续段的 \(l\) 合并考虑。设连续段长度为 \(k\)，你每次要做这样的事情：

• 在 \(f_l\) 前添加 \(k\) 个 1
• 做 \(k\) 遍从连续段右端点到 \(R\) 的前缀和（实际上需要插板法），其中 \(R\) 为 \(f_{l,r}\) 有效的最大的 \(r\)

第二个可以用 NTT 优化。

复杂度 \(O(|\sum| n\log n)\)

7.4 模拟赛1

7：50 T1 想法

8：15 T1 bug

9：20 放弃 T1

10：00 T2 60

11：00 T3 暴力

11：30 回到 T1

(t1 = div2t1, t2 = div1t1)

60 + 60 + 15 + 25 。除了 T1，其他题目和考时预估一致。

---

T1 失败在第一步，认为所有的区间都会移动某一段距离并跨过一个固定点 x。

容易想到从小到大排序按顺序处理放左/右，但是发现转移的贡献和 最终放左边的总个数-放的时候左边的个数 有关，这意味着需要枚举左边放了几个。

顺势写出 n^3，瓶颈在于枚举左边放了几个，可以发现单峰，那么 n^2log。

1. 可以有区间不动 \(\to\) 贡献计算方法错误
2. 为了处理枚举左边放置个数的问题，可以 （思维盲区）从小到大 \(\to\) 从大到小处理！

所以实际上给出的是一个假算法，只是数据良心给了 60pts

---

T2 没啥好说的，失败在不会杜教筛，现在会了/hanx

---

T3 好题，首先误认为 字典序 等价于 26进制数。

正是因为这个误导，导致我认为不可以倒着从 T 开始 DP，然后发现正着也不可以，然后不会了。

正解：

枚举 T，预处理 T 的所有答案。记 f_i 表示 i 是起点的答案。

f_i 如果记录整个字符串的话，首先空间肯定是不可以的，所以改为记录 \(next_i\) 表示 \(f_i\) 是通过 \(f_{next[i]}\) 转移而来。

可以发现 next 最终形成一个以 T 为根的内向树。

考虑往树上新增加一个点 i，需要做 出边次 字符串比较，字符串比较应当使用 hash + 二分求 lcp 的方法，为了获得 hash 值，采用的方法是 树上倍增代替二分，即算出 \(hsh[j][k]\) 表示从 j 开始，长度为 2^k 的字符串的 hash 值。

对于一个 T，这样的比较做 \(m\) 次，总复杂度 \(O(nm\log n)\)

只能在稀疏图上通过，稠密图有点难。

暴力维护 fi(也就是next) 数组的 rk 数组，有 O(n^3) 的算法。

感觉这个思路比较类似 dijkstra 加不加堆优化的问题，加了堆优化，那么稠密图会 G，一个道理。

---

T4：明天再补。

7.5

[Ynoi2007] tmpq

昨天 T4 原题。

根号分治+根号平衡

发现题目给的 b[a[i]] 和 c[a[i]] 并没有什么性质，所以可以直接将题目看成是给定 a,b,c，每次执行 3 个单点修改，题目变成了数有多少个出现顺序是 b a c 的相同颜色对。

暴力 \(O(n^2)\) 做：

答案可以表示为 \(\sum_{col} \sum_i pre[col][i - 1] suf[col][i + 1]\)，每次询问的时候，暴力把每种颜色提出来，扫一遍。

注意到修改只有 \(O(q)\) 个，颜色有 \(O(n)\) 种且贡献独立，应当想到根号分治。

• 出现次数 \(\le B\) 的颜色

考虑执行上方的暴力，但是问题是，上方的暴力实际上是对于单个颜色，每次需要花费 \(O(B)\) 的时间可以问出在 r 的答案，现在需要对多个颜色做，那么这样的复杂度显然是错误的，比如 r = n。

仔细思考，发现对于一个颜色而言，相邻两个出现位置之间的答案是一样的，是一个区间修改的形式；而每次求在 r 的答案就是执行一次单点查询。

那么，需要快速的维护某一个颜色以每一个出现位置为 r 的时候的答案，由于需要处理 suf，所以上面的暴力自然是落伍的。

自然考虑一个前缀 DP，维护 b, ba, bac 的数量。维护所有出现次数满足条件的颜色的出现位置，每次对某一个颜色进行修改的时候，暴力重新跑这个前缀 DP，然后做区间加。

分析一下，区间加执行 \(6qB\) 次，而单点询问只有 q 次，那么容易执行一个 \(O(1)\) 修改，\(O(\sqrt n)\) 询问的根号平衡。

综上，这一部分的复杂度是 \(O(qB + q\sqrt n)\)，其中 \(qB\) 大概带了 12 的常熟。

• 出现次数 \(\ge B\) 的颜色

由于这样的颜色数量不太多，那么赋予了我们每次询问都遍历这些颜色的权利。

方便空间，先把这部分的东西离线下来，遍历每一个颜色处理，每次的事件形如 在某一个位置出现/消失某一个类型(abc)，或者说询问 r 的答案；前者出现 \(O(q)\) 次，后者 \(O(\frac nB q)\) 次。

一个自然的想法是用线段树维护一个动态 DP，这样愚蠢的地方在于忽略了询问次数更多，这样的修改询问的复杂度是一致的。

那么，现在需要使用的是一个 \(O(\sqrt C)\) 修改，\(O(1)\) 查询的根号平衡。需要维护前缀块的 b, ba, bac 之类之类（需要维护一点更多的信息以快速合并两个部分）。

这一部分的复杂度是 \(O(q\sqrt C + \frac nBq)\)

总复杂度是 \(O(q\sqrt C + \frac nBq + qB + q\sqrt n)\)，当然有一点 set 之类的 log，用力调块长可以通过。

「AGC048D」 Pocky Game

题目很区间 DP ，那么设 \(f[i, j, k]\) 表示区间 \([i, j], a[i] = k\) 是否先手必胜。

状态数显然爆炸，感性理解如果 \(f[i, j, x] = 1\)，那么 \(f[i, j, x + 1] = 1\)，所以改为设 \(f[i, j]\) 表示使得 \([i, j]\) 是先手必胜， \(a[i - 1]\) 至少是多少；对称地设 \(g[i, j]\) 表示后手必胜。

探究一下游戏过程，对于局面 \([l, r]\)，考虑左边需要增加至少多少个石头才能使得先手必胜。

• 后手希望的是达到 \(g[i, r - 1] <= a[r]\)，也就是希望尽量消耗 a[l - 1]，于是先手会一个一个取 a[l - 1]，后手也会一个一个取。

• 希求先手必胜，那么后手当后手发现下一步 a[r] < g[l, r - 1] 的时候，他会直接将 a[r] 取空，因为下一步先手必然会直接取空 a[l - 1]，从而让后手导向了 [l, r] 的必败态，所以后手一定要提前取空 a[r]，以争求进一步消耗 a[l - 1]。

• 这样的消耗过程会一直执行，直到某一个 a[i] 初始的时候就已经 < g[l, i - 1]，那么后手求大了。

综上，可以发现

\[f[l, r] = \sum max(g[l, i - 1] - a[i] + 1, 0) = f[l, r - 1] + max(g[l, r - 1] - a[r] + 1, 0) \]

g 的转移是类似的。

「AGC043C」Giant Graph

发现点权是很特殊的形式，于是可以考虑贪心。

首先取 \((n, n, n)\)，然后执行类似 BFS 的过程，能取则取。

也就是说对于一个点，如果相邻的点都没选，那么就选；否则不能选。

等价于 \((n, n, n)\) 是必败态，求必败态的权值和。

由于每次只能移动一个维度，所以可以看成是独立的三个棋子，那么需要求出三个图 SG 值，问题是求 \(\sum _{x\oplus y\oplus z = 0} f(x)g(y)h(z)\)，f,g,h 表示 \(SG = x\) 的数量。

由于 SG 值最多达到 \(\sqrt m\)，所以可以暴力求解 f, g, h。

「CF1091H」New Year and the Tricolore Recreation

有趣的题目。

第一眼看发现并不是公平组合游戏，无法使用 SG，那 G 了。

但是仔细思考一下，每次都想成中间的棋子不动，那么操作转化成要么把左边动 d，要么把右边动 d，这就是一个公平游戏了！

剩下的事情是计算 SG 值，SG 值不会太大且每次转移是固定的，使用 bitset 优化。

开 SG 值个长度为 n 的 bitset，$B[val][i] = 1 $ 表示 \(SG[i]\neq val\)

[CF850C]Arpa and a game with Mojtaba

对于每一个 p 暴力计算 sg 值，用一个 bitmask 记录是否存在 \(p^k\) 。下面证明状态数较少

考虑对于一个最高二进制位为 \(k (0<k<32)\) 的 bitmask

计算由他延申出来的最高二进制位为 m 的状态数量

• 当 \(m<k/2\) 时，就是 \(2^m\)
• 当 \(m>k/2\) 时，考虑怎么操作可以使得 \(m^{\prime}\) 依然大于 \(k/2\) ，发现只能是砍去 \(>k/2\) ，或砍去 \(< m-k/2\) ，只有 \(2*m-k\) 个 bit 位可以砍，所以子状态数为 \(2^(k-m)\)

这样算的话大概在 \(2^17\) 级别，非常可以接受

「CF494E」Sharti

经典颜色反转博弈 Trick。SG 值等于所有白格的 SG 值异或和。

打表？？发现 \(SG(x,y) = \min\{lowbit(x), lowbit(y), highbit(k)\}\) ，枚举二进制第 i 位，剩下一个矩形并的问题，扫描线即可。

重温扫描线，注意离散化的问题，线段树节点代表的是数轴 (l - 1, r]，所以离散化的时候，对于修改 [l, r, y]，需要把 l - 1 和 r push_back 进入 vec，然后 lower_bound 找到正确的值

「HNOI2010」取石头游戏

发现如果 a < b > c，那么这三个可以缩成同一个数，因为先手取 a，那么由于后手知道先手不是 sb，也就是说外面没有更好的选择了，所以取 b 肯定不劣，另起炉灶是危险的；那么先手就已经亏了，所以取 a 的目的就是取 c，所以必然拿 c。

对于开头的第一个段，可能剩下一个单调递减的段，谁取谁 sb；对于最后一个段同理；其他的部分，都应该形如一个单谷，双方都会贪心取这些单谷的两头。

发现开头/末尾的贡献是固定的，那么提前算出来，加入堆中即可。

自己尝试的丑陋的代码实现 WA 在于存在 abcde-> abe -> e (abc 不可以缩)

7.6 模拟赛 2

7：50 纵览

8：10 T0 想法

9：30 心态爆炸

10：20 T1 结束

11：00 T2 bug

11：40 T2 结束

这把纯纯 joker 场，除了 T3 非常神笔有点不可做，其他的题感觉都没有什么思维难度。

考场预估：0 + 100 + 100 实际：0 + 100 + 30

感觉今天代码实现犯了很多错误，大部分时间都是在调 bug，体验非常差。

这场充分暴露自己对于算法不熟悉（忘记）的问题

---

T0：看到保证 \(w(i, j) \neq 1\) 的部分分，发现只需要维护 0 边的图，然后想到如果只有增加 0 就好了，顺其自然的有了线段树分治。

加上 1 怎么办，一个简单的想法是知道路径一定是 一段0 + 一个1 + 一段0，那么只需要维护反图，找到 u 可到的集合 S， v 可以到的集合 T，遍历 S，判定是否存在一个 1 边即可。

上述的操作都可以用 bitset 优化，算下来复杂度是 \(O(\frac{n^2mlog q + n^2q}w)\)

以为能过，9：30 发现一直过不了大样例，心态爆炸。

实际上：

1. n^2q/w 是过不了的。
   2。 过不了大样例的问题在于线段树分治写错了，由于是对初始图预先跑了传递闭包，所以初始图里面不能包含可能会消失的边；其次，不需要预先跑传递闭包。

因为 n^2q/w 过不了，所以需要也需要维护 1 的图，有两种思路：

1. 搞一个分层图，层与层之间靠 1 边链接，如果 (u, v) 联通，dis = 0；如果 \((u, v^{\prime})\) 联通，dis = 1。
2. 设 \(f[d][i]\) 表示点 i 花费 d 可以到的点的集合。

其实可以发现两种思路本质相同。

整个过程中出现的 joker 现象：

1. 认为判断距离 1 的方法是 f[0][u] & rev[v]，即 u 走一段 0，最后一步是 1，但是实际上 1 可以是中间某一步
2. 负下标
3. 处理 1 的方案是维护反图，但是复杂度是 n^2q/w，纯纯 T 飞
4. dijkstra 堆优化的 cmin 没有 return
5. 普通 dijkstra 每次找一个 dis[x] = min dis[i] 更新其他 dis 后，没有让 vis[x] = 1
6. 认为那些从始至终都出现的边应该在最开始的时候跑传递闭包以保证复杂度的问题
7. 正反图下标写反
8. 传递闭包初始值没有设

---

T1：简单构造，由于知道网格图和组合数的关系，容易往组合数方向思考。

bug: rx 和 x 写反。

---

T2：考场上搞了一个 n\sqrt n，交上去没有关调试行，只有暴力 30，实际上有 60。

bug：仿照 SG 函数开 vis 的时候，每次没有 ++ tim。

nlog^2n 的做法是优雅的，经过 张佳艺同学提出的问题 重温了动态开点线段树的知识

7.7 whq 杂题

感觉今天的题都很怪，上午磕磕绊绊地听懂一部分，下午开始写。

前面三道比较顺利，反思一下做 T4 [ICPC2017 WF] Replicate Replicate Rfplicbte。

从 6:00 开始想，7：30 心态开始爆炸，8：10 心态平稳 ，8：40 给 zqm 讲，发现 zqm 一直领会不了我的意思，开始急急急，9:00 给它贺了，9：50 依旧没有找到问题到底在哪里。

心态波动的原因在于太过于在于做题速度了，总想着快点吧题目列表尽量多弄一点是一点，导致可能很多细节都没有想清楚就开始写，写完发现出了问题，没有仔细地探求思考问题的原因，而是在漫无目的地乱找 bug，虽然这个 bug 所表现出来的调试信息的确有一定的误导性。

背后折射出来的是最近可能有一些压力，反映出思想境界不够的问题。

---

[BalticOI 2011 Day2] Tree Mirroring

考虑如果找到了两个对应点，那么从这两个对应点跑两个 bfs，可以根据距离关系判断 叶子/左右侧

划分出两个集合之后，剩下的事情大概是判断树的结构对不对，可以按照 top 序对两个集合重标号，要求对应点的 fath 相同。

问题是如何找到一对对应点。

考察随便一个环，发现如果把这个环上的边断掉，那么剩下的每一个连通块只会同时包含环上至多两个点，且这两个点就是所求。

注意特判一下度数之类的问题。

CF360E Levko and Game

一条边，只有选 l 和选 r 两种可能，因为只会有利于某一方。

首先可以跑一个最短路，假如点到 S1 更近，那么采用 l，否则采用 r。

问题是存在到两点距离相同的情况，这个时候存在的情况是假如选择 r 的话，那么可能会便宜了对方，因为可能自己并没有其他的好路可走，但是也可能便宜自己；假如选择 l 的话，那么对双方而言，答案都会趋近于一致，即都会倾向于走同一条路。

也就是说，选择 r 代表着尽可能求变，且可以知道如果全部都选 r 的时候无法获胜，那么某一部分改选 l 肯定也赢不了。所以可以先把所有边都设置 r，然后试一下可不可以赢。

如果不可以，那么就要求平，全部选 l 试一下即可。

Gym100531K Kebab House

题意：

数 01 序列，长度为 \(\sum q_i\)

• 要求 \([1, q_1]\) 中至少有 \(x_1\) 个 0，\([q_1 + 1, q_1 + q_2]\) 中至少有 \(x_2\) 个 0。

• 相邻两个 1 之间至少有 \(t\) 个 0

设 \(f_{i, j}\) 表示填完了前 \(i\) 段，下一段开头至少需要 \(j\) 个 \(0\) 的方案数（实际上确定了第 \(i\) 段最后一个 1 的位置）

状态数是 \(nt\) 的，如果转移是 \(O(t)\) 就好了。

考虑计算 \(a_{i, j}\) 表示 \(f_{p, i} \to f_{p + 1, j}\) 的转移系数。对于 \(j > 0\)

\[a_{i, j} = [i = q + j] + \sum_{k = 0}^{q - x - 1} \binom{q_{p + 1} - i - (t - j) - 1 - t \times k}{k} \]

枚举除了处于 \(q - (t - j) - 1\) 位置的 \(1\) 之外，还有 \(k\) 个 \(1\)，那么先填上 \(kt\) 个 \(0\)，剩下 \(q - i - (t - j) - (k + 1) - t\times k\) 个 \(0\)，需要放到 \(k + 1\) 个可空盒子中。

注意到上式只和 \(i - j\) 有关，且组合数上标带了一个 \(-tk\)，所以可以做到 \(O(\frac qt)\) 的时间求出一条斜线的转移系数，总体就是 \(O(q)\)，做 \(n\) 次就是 \(O(nq)\)

剩下一个 \(j = 0\) 的情况不成问题。

[ICPC2017 WF] Replicate Replicate Rfplicbte

假如没有出现 bug，那么可以借助当前 \(n\) 行 \(m\) 列的 \(S\) 的 \((n - 2) \times (m - 2)\) 的部分还原出上一步 大小 \((n - 2) \times (m - 2)\) 的 \(T\)。

出现了 bug，现在的担心是会不会多个 T ，经过 bug，可以到达同一个 S，导致我还原得并不对。

但是这种情况是不会出现的，因为假如 S 出现一个 bug，考虑在边角的情况，至少会使得 T 变成：

XXOXXO...
XX
O

和 ans 的位置差 \(\ge 4\)，但是我只有一个 bug 的机会，所以改不动，与假设矛盾。

现在的问题是如何找到 bug，假如没有 bug，则矩阵的最右两列和最下两行应该全为 0。但是因为 bug，最右两列和最下两行中可能会出现 \(1\)

由于我们知道一个 bug 的影响是形如上方的形状，即两行/列之中必有一个 X，所以根据最右两列和最下两行中的 1，我们可以唯一确定该位置，或者判定其不合法。确定出锅的位置后，只需撤回其影响即可。

CF1616G Just Add an Edge

注意题目给出的性质，自然想到先提出一条 1 到 n 的链出来。

假如本来就存在哈密顿路，那别玩了。

对于一个合法的情况，可以是 \(1\stackrel{add\ one}{\longrightarrow} y - 1 \leadsto x \to y \leadsto x + 1 \stackrel{add\ one}{\longrightarrow} n\)，其中，要求 \(y - 1 \leadsto x\) 和 \(y\leadsto x + 1\) 两条路径不交，且并集是 \([y - 1, x + 1]\)。

称上面这个状态叫做 \((y - 1, y)\) 可达 \((x, x + 1)\)；还有一种合法的可能是 \((y - 1, y)\) 可达 \((x + 1, x)\)，此时需要加边 \((x + 1, y)\)

考察一下这个并集到底是咋并出来的，可以看成是两种颜色交替出现，画一画，发现：

\((y - 1, y) \to (p_1 + 1, p_1) \to (p_2, p_2 + 1) \to (x + 1, x)\)

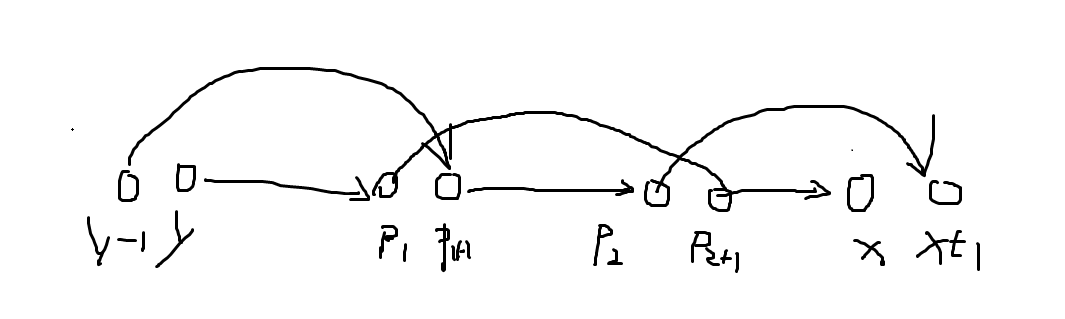
这个格式，一看就很 DP，因为状态可继承。而且每次必定切换顺序。

所以枚举起点 \(y\)，设 \(f[i][0/1] = 0/1\) 表示 \((y - 1, y)\) 到 \((i, i + 1)/(i + 1, i)\) 的可达性，转移形如：

\[f[i][c] \to f[j][c \oplus 1] \quad when\ exist\ i\to j + 1 \ \&\&\ i + 1\stackrel{add\ one}{\longrightarrow} j \]

这样子搞下来，复杂度最优是 \(O(\dfrac{n^2}w)\) ，难以通过。

复杂度瓶颈在于枚举 \(y\)，联想到 Graph Problem with small n 中曼哈顿路径拆成 \(x \leadsto 1\leadsto y\) ，拆成 \(1\leadsto x,1\leadsto y\)，考虑找到这样一个合适的 1

发现如果某一个 \(p\) 使得 \(p \to p + 1\) 是断开的，我们发现这个 p 就很适合作为 1，因为不存在一个 DP 转移，使得 \(i < p, j > p\)，所以 p 的两侧是独立的。

不妨设 \(p\) 是所有这样的断点当中最小的一个。

考虑怎么计算答案，设 \(lst\) 是最靠前的位置使得 \(lst \stackrel{add one}{\longrightarrow} n\)，那么只需要考虑 \(y \le p + 1, x\ge lst - 1\) 的对。这样的对合法当且仅当 \(f_{x, 0} \cap f_{y - 1, 0}\) 或者 \(f_{x,1}\cap f_{y - 1, 1}\)，注意这里 \(0/1\) 一定要对应，不然无法保证中间走的路径是合法的。

由于一对 x, y 只会算一次，所以这里存在一点算重的问题，稍微处理一下就好了。

有一点细节。

[CF1361E]James and the Chase

\(20\%\) 意味着出现频率比较高，意味着可以加一点随机化之类。

不知道怎么想到的，类似 [BalticOI 2011 Day2] Tree Mirroring 一样，假装自己知道一点东西，然后怎么做。

在这里，假装自己已经知道了某一个点是好的，自然，提出一颗以它为根的 dfs 树，由于当前点是好点，性质是没有前向边。

考虑另外一个点是好的，那么要求子树内最多有一条跨越当前点返祖边，且如果有一条，那么当前点是否是好点取决于那个祖先是否是好点。

这个玩意还算是比较好做的，搞一个树上差分啥啥的就可以了。

唯一的问题是如何找到第一个点，随机化之后暴力 check 是否有前向边即可。

「WC2019」数树-> strange trees

CF1672G Cross Xor -> https://www.fzoi.top/problem/7075

7.8 whq 组合计数

前面听组合意义听得非常振奋，后面可能是听麻木了，导致对于一些厉害的步骤有点迟钝无感。

同时充分印证了昨天晚上所反思的问题，太着急了，整个人处于焦虑的状态，导致今天上午虽然听的很爽，但是还是觉得自己做得不够，导致心烦意乱。但是实际上，这种解决问题的过程就已经是幸福本身，焦虑是附加的。

焦虑是不对的，焦虑的原因是对现状不满意，而焦虑，作为对于这一情形的反应，表现出退缩与懦弱。

[ARC110D] Binomial Coefficient is Fun

简单组合数，题目式子是：\(\sum_{\sum b <= m}\prod \binom {b}{a}\)

组合数，考虑转成二维平面走路径问题，

\[\sum_{\sum b <= m - \sum a}\prod \binom {a + b}{a} \]

那么，设 \(\sum b = x\)，这下子就等价于走到 \((\sum a, x)\) 的方案数（一条路径唯一拆成若干个矩形），组合数随便算算。

[ABC221H]Count Multiset

比较巧妙的题目，看到递增序列，考虑差分数组

首先可以有一个 naive 的 dp：\(f_{i, j, k}\) 表示考虑到 \(v = i\)，一共选了 \(j\) 个数，值和为 \(k\) 的方案数。转移 \(f_{i, j, k} \to f_{i + 1, j + t, k + (i + 1)t}, t\le M\)

这玩意一看就不好优化，仔细算算复杂度发现是 \(O(n^3\log n)\) ，多少需要砍掉一个 \(O(n)\),那怎么办！

上述实际上刻画了一个单调的序列，考虑转而对他的差分数组进行 DP，现在的要求是不能有连续的 M 个 0。

第一反应设 \(f_{i, j}\) 表示填了 \(i\) 个数，和为 \(j\) 的方案数，转移是多开一维 \(0/1\) 标识上一次转移的是/否是 \(0\) 段：

\[f_{i, j, 0} \to f_{i + 1, j + v, 1}\\ f_{i, j, 1} \to f_{i + 1, j + v, 1}\\ f_{i, j, 1} \to f_{i + t, j + t(cnt - i + 1)} ??? \]

发现第三个转移很假，你 cnt 是啥啊。

对于这个差分数组 \(b_i\)，要求是 \(\sum b_i(cnt - i + 1) = n\)，反转一下，\(\sum b_ii = n\)，这个技巧上一次见到是在 7.4模拟赛 T1。

那么可以写出更为干净的转移：

\[f_{i, j} = \sum_{k \ge i - m, t} f_{k,j - it} \]

即是说枚举 \(b_i = t\)，上一个 \(b_i \neq 0\) 的位置是 \(k\)，可以将第一维前缀和优化，复杂度砍下 \(O(n)\)

现在，回溯性建构一下，发现之所以维护差分数组可以优化这个 DP，是因为去除了选择的数单调递增以避免算错这样的一个限制，从而导致不需要记录当前考虑到的值的大小。

CF1204E Natasha, Sasha and the Prefix Sums

最大前缀和求和。

看到是最大值求和，觉得很烦，改成求 \(\sum f_i\) ，表示 \(\ge i\) 的方案数。

这样就好办多了，容易转化成二维平面上的路径问题，然后翻折一下就好。

[NOI Online #2 提高组] 游戏

简单二项式反演 + 树形 DP 随便做

AGC058D Yet Another ABC String

nb 容斥。

即我们钦定有 \(i\) 个极长不合法子串的起点。

极长不合法子串的长度还不确定，但是我们发现只要钦定它们的长度 \(\ge3\)，即每个字母至少出现一次即可。

于是我们现在相当于有 \(a−i\) 个 \(A\), \(b−i\) 个 \(B\)，\(c − i\) 个 \(C\) 是自由的。我们需要把它排成一个初始串 。这部分的方案数是多重集排列。

然后，我们需要把 $ i$ 个串，每个都是 \(ABC,BCA,CAB\) 中之一 的串插入一开始排成的那个初始串。如果插入的位置在开头，那么 3 个串都可以被选择插入；如果在中间，因为我们 容斥的是极长不合法子串的起点，也就是说它们必须是起点，其他的可以是也可以不是，所以我们不能接在字母序上一个字母后面，导致这个字母成为了起点。

具体一点，ABC 不能接在 C 后面，BCA 不能接在 A 后面，CAB 不能接在 B 后面。我们发现无论插入位置前一个字母是什么，插入的串都有 2 种选择。

分讨一下计算贡献就好。

[JLOI2015] 骗我呢

翻折引理

发现对于每一行来说，一定只有一个位置 \(\Delta = 2\)， 其他位置 \(\Delta = 1\)。

设这个位置叫做 \(p_i\)， 题目要求等价于 \(p_i >= p_{i + 1} - 1, p_i\in[1, n]\)，计数 \(p_i\)

这个 \(-1\) 看着很丑陋，考虑平移一下，变成计数 \(p_i \ge p_{i + 1}, p_i\in[(n - i) + 1, (n - i) + n]\)

考虑组合意义，这下子就可以清明地看出来，问题等价于从 \((n, 2n - 1)\) 向下向左走到 \((1, 1)\)，不能跨过直线 \(y = n + 2 - x\) 和 \(y = 2n - x + 1\)，翻折引理即可。

CF961G Partitions

\[\begin{align*} ans&=\sum_R \sum_{S\in R} |S| \sum_{x\in S} w_x \\ &= \sum_x w_x \sum_{S} |S| {{n - |S|}\brace{k - 1}} \binom{n - 1}{|S| - 1}\\ \end{align*} \]

只考虑后面的 \(sum\)，思路是把 \(|S|\) 看作是 1 联通块内每一个点才会有的贡献，那么 \(binom\) 就是在枚举这个联通块。

\[\begin{align*} &=\sum_{S} |S| {{n - |S|}\brace{k - 1}} \binom{n - 1}{|S| - 1}\\ &= \sum_s {{n - s}\brace{k - 1}} \sum_{|T| = s, 1\in T}s \\ &= \sum_s \sum_{|T|=s, 1\in T}\sum_{i = 1}^n [i\in T]{{n - s}\brace{k - 1}}\\ &= \sum_{1\in T}\sum_i {{n - |T|}\brace{k - 1}}[i\in T]\\ &= \sum_{i = 1}^n \sum_{\{1, i\}\subset T} {n - |T|\brace k -1}\\ &= {n\brace k} + (n - 1){n - 1\brace k} \end{align*} \]

「BZOJ 2159」Crash 的文明世界

k 很小，考虑使用斯特林数把复杂度搞到 k 上。

\[\begin{align*} S(x) &= \sum_{i = 1}^n f_x(i)^k\\ &= \sum_{i = 1}^n \sum_{j = 0}^k \binom{f(i)}j j! {k\brace j}\\ &= \sum_{j = 0}^k {k\brace j}j! \sum_{i = 1}\binom{f(i)}j \end{align*} \]

设 \(g_{x, j} = \sum_{i = 1}\binom{f_x(i)}j\)，只需要求出 \(g\) 就好。

\(\binom{f(i)}j\) 的意义是在 \(f_x(i)\) 条边中选出 \(j\) 条的方案数，考虑 DP 求 \(g\)

先考虑计算 \(g_1\)。

设 \(dp_{u, j}\) 表示 \(\sum_{v\in subtree(u)} C(f_u(v), j)\)，考虑 \((u, son)\) 这条边，选和不选都对应了一种贡献方式，实际上把组合数的系数拆到了状态数上（拆到每一个 \(u\) 进行决策），所以 \(dp_{u, j} = \sum_{v\in son} dp_{v, j} + dp_{v, j - 1}\)

那么 \(g_{1, j} = dp_{1, j}\)，剩下的显然是一个换根 DP。

CF997C Sky Full of Stars

相对简单的容斥题，暂略。

[MtOI2018] 情侣？给我烧了！

理解了很久生成函数做法，勉强看懂，但是存在更为优雅的组合意义做法。

illusory_dimes

7.9 晚自习

回来准备补总结，但是发现欠的总结有点多，补了一会儿不想弄了，随便做做题，看了看 ARC。

ARC164D

分析可以发现一个电荷的移动方向在起始的时候就确定了

具体的，\(F(i) = c_i \times (sum[i - 1] + sum[i])\)，这是因为总和为 0。

一个考虑是枚举二元组并计算贡献，但是发现这样不好算。

solution：

直接一起计算，稍微画一画可以发现实际上是一个括号序列的变体，本来是钦定左右括号是啥，现在是 stack 里面谁更多，谁就是左括号。

由题目性质，知道这样肯定存在合法匹配。

假如当前有 j 个左括号，加入一个左括号会使得总距离 + j；加入一个右括号会使得总距离 + j。

所以可以设 g[i][j] 表示处理了前 i 个，sum[i] = j 的答案，f[i][j] 表示方案数，有：

if(s[i] != '-') f[i + 1][j + 1] += f[i][j], g[i + 1][j + 1] += g[i][j] + abs(j - n) * f[i][j];
if(s[i] != '+') f[i + 1][j - 1] += f[i][j], g[i + 1][j - 1] += g[i][j] + abs(j - n) * f[i][j];

7.10 gyr 杂题

[ABC306Ex] Balance Scale

主旋律的儿子题的儿子题 孙子题

假装我们已经枚举那些为 = 的边了，剩下等价于对图定向使得为 \(DAG\)，这个方案数计算是经典的，思路是考虑每次剥去度数 \(= 0\) 的点。

设 \(f(S)\) 表示 \(S\) 是 \(DAG\) 的方案数，枚举砍掉 \(T\) 集合，\(T\) 是独立集，出现的算重的情况是 \(f(S\backslash T)\) 中还有残余的同级 \(0\) 度节点。

也就是说，这样计算，实际上是每次钦定了一个集合 \(T\) 是 0 度集合，那么套一层二项式反演，钦定 \(T_1\) 是 0 度，枚举恰好 \(T_1\subseteq T\) 是 0 度。

\[f(S) = \sum_{T_1\in S, \varnothing \neq T_1} \sum_{T_1\subseteq T} (-1)^{|T| - |T_1|} ok[T]f(S\backslash T)\\ = \sum_{T\in S, \varnothing \neq T} ok[T]f(S\backslash T)\sum_{T_1\subseteq T} (-1)^{|T_1| - |T|}\\ = \sum_{T\in S, \varnothing \neq T} (-1)^{|T| + 1}ok[T]f(S\backslash T) \]

其中 \(ok[T]\) 表示 \(T\) 是独立集。

加入 \(=\) 的考虑，考察每次枚举的 \(T\)，上述计算需要这 \(T\) 个点之间构成独立集，即这 T 个点之间不能有 \(>/<\) 的边，但是可以有等于的边。

那么，也就是说，可以不必要 \(ok[T]\) 这个条件，而直接将所有边都搞成 \(=\)。

简单的删掉 \(ok[T]\) 会导致新的算重的问题，对于一个独立集，如果增加一个与这个独立集独立的联通块，此时并不会新增加一种定向/定等于的方案，这里算重了，按理说应该是交给容斥系数来解决的问题，但是这里的容斥系数是 \((-1)^{|T|-1}\) 就一眼假。

记 \(c(T)\) 表示 \(T\) 的生成子图的联通块个数，发现如果 \(c(T)\) 是容斥系数就很真，可以理解，相当于以联通块作为元素单位。

计算的是生成子图而不是导出子图之类，所以实际上保证枚举的 = 的方案是全的之类之类。

CF1081G Mergesort Strikes Back

神必期望题，考察对概率的理解。

深度为 \(k\) 时，段长度只有两种，设为 \(a,b\)，分别有 \(ca, cb\) 个。

问题就是 对这 \(ca + cb\) 个段进行合并，求期望逆序对个数。

考察一个段，发现如果这个段内的某一个前缀最大值进入最终的序列，那么段内直到下一个前缀最大值之间的数字也会入队。

计算逆序对数量，由期望线性性，计算 \((i, j)\) 成为逆序对的概率。

如果 \(i, j\) 在同一个段，这部分是容易的。

如果 \(i, j\) 分属长度为 \(a, b\) 的段， 设 \(i > j\)，记 \(a_i, a_j\) 分别表示 \(i, j\) 各自所属的前缀最大值的值，\((i, j)\) 成为逆序对当且仅当 \(a_j > a_i\)

记 \(p_i, p_j\) 为 \(i, j\) 在其所在段中的下标。

考虑这 \(p_i+p_j\) 个数中的最大值 \(w\)，它只能落在严格位于 \(j\) 之前的 \(p_j−1\) 个数中，且要求 \(a_j > a_i\)，概率是 \(\dfrac{p_j - 1}{2(p_i + p_j)}\)

剩下的事情，可以通过推柿子然后预处理一些东西使得复杂度满足需求。

Gym104197N No Zero-Sum Subsegment

挺有意思的题

题目条件等价与同一个前缀和不能出现两次，自然转化到二维平面上走折线。

发现如果 \(x - 1, x, x + 1\) 都出现过，那么如果当前 \(sum > x\)，\(sum\) 不可能 \(< x\) 了，因为恶跨不过去; \(sum < x\) 的时候同理。

那么一定是先降到某一个负数，然后跳上来，然后跳到某一个点，降到 sum。

• 先降再升：-2-2-2-1+2+2+2+2 / -2-2+1+2+2
• 先升再降：+2+2+2-1-2-2-2-2 / +2+2-1-2-2
• 升：+1-2+1/+1/+2

需要枚举的东西其实不是很多，推推柿子。

[CF1712F]Triameter CodeForces

使用了去二分化的思想，每次咕咕咕咕。

7.10 wzy 构造

抽屉原理

[CF1450C2]Errich-Tac-Toe (Hard Version) 如下三种构造都是合法的且操作总数为 k：将 \((i + j) \bmod 3 = 0/1/2\) 的涂黑

[Gym102900B]Mine Sweeper II 雷和空地交换之后，答案不变，用好做的做。

[CF1364D]Ehab's Last Corollary 题目给出的两个问题显然是互斥的，随便做

提出无向图的 dfs 树

dfs 树上的非树边只会是反祖边，这会提供很多有用的性质。

「IOI2019」景点划分 提出 dfs 树，考虑重心，先给 A 分配，再给 B 分配，啊啊啊啊啊

[CF1470D]Strange Housing 提出 dfs，然后乱染。

CF1391E Pairs of Pairs 发现如果选择两个深度相同的点作为 pair，那么这样是非常安全的。对最大深度进行讨论，考虑最大深度 \(<\lceil\frac n2\rceil\)，那么每层最多留下一个点没有配对，最多有 \(\lfloor \frac n2\rfloor\) 个点没有配对，符合需求。

CF1270G Subset with Zero Sum

非常厉害的题目，赛时卡了 tourist

由于 \(i−n≤a_i≤i−1\)，所以 \(1≤i−a_i ≤n\)。

建立一张 \(n\) 个点的有向图，对于每个点 \(i\)，连边 \(i→i−a_i\)

这张图中每个点的出度都为 \(1\)，因此这张图是一个基环内向森林。

可以发现对于任意一个环，环上的点对应的下标就是我们要找的答案。

7.13 wlx 字符串

没看懂 AGC060D Same Descent Set

看了一下今天 Div1 考试的 T12，T1 是一个挺有意思的 DP，T2 没看懂

div1 T1 数(count)

给定 \(n, m\)，求满足以下限制的长度为的序列数目:

1. 每个元素在 \([1, m]\) 之间；
2. 一次操作定义为删除一个长度至少为 2 且区间两端相等的区间；

该序列需要在若干次操作内被删空。答案对 \(10^9 + 7\) 取模。

很有意思的题，第一眼看过去可能就喜欢开始区间 DP，但是通过经验，这种看起来可以区间 DP 的题目，区间 DP 大概都是很难做的，要么复杂度太高，毕竟状态数放在那里；要么很容易算重。

发现一旦前面放了一个数字，使得当前的序列不合法，那么在当前序列后面如果不放 使得当前序列不合法的第一个数字之前的数字，那么还会是不合法。

这可能就启发了这样一个 DP，考虑做前缀 DP，即考虑顺次放数。

设 \(f_{i, j}\) 表示填了前 \(i\) 个数，当前序列不合法，填 \(j\) 种数可以使得序列合法的方案数。

自然的，设 \(g_{i, j}\) 表示填了前 \(i\) 个数，当前序列合法，填 \(j\) 种数可以使得序列仍然合法的方案数。

自己推一推转移：

\[\begin{align} f_{i, j} \times j &\to g_{i + 1, j}\\ f_{i, j} \times (m - j) &\to f_{i + 1, j}\\ g_{i, j} \times j &\to g_{i + 1, j}\\ g_{i, j} \times (m - j) &\to f_{i + 1, j + 1} \end{align} \]

啦啦啦～

7.14 模拟赛3

9：30 放弃 T1 三分

10：00 写出 T1 几何做法，从未有如此美妙的开局！

11：20 放弃 T2，大样例跑了 6s！

今天纯纯被 T1 毒死。

T2 < T1 < T3 < T4。

---

T2

单调栈计数的一个关键注意点：

上来管都没管就先写了一个单调栈摆上去，但是发现自己在有多个相同值的时候似乎不会算，会计算重复，直接把单调栈删了。

但是实际上是可以算的，比如，对于序列 111 需要使得处理出来的使得它是区间最小值的“控制区间” 是：

L[1], R[1] = [1, 3];
L[2], R[2] = [2, 3];
L[3], R[3] = [3, 3];

也就是左边的相同点视作小于，右侧的相同点视作大于。

---

T3：套路题，\(andsum, orsum, gcd\) 的变化量是 \(O(log)\)

T4: 简单分讨之后线段树随便维护。

回顾 按位或，随机游走，有意思。

7.15

UNRD1 + 口胡 luogu 月赛label

不知道如何做：

有一个排列和先后手，每个人每次可以把 [1,p1] 区间里面的数随意重排，但是不能使得新的 p1 是之前出现过的数字。计数后手必胜。

7.17 模拟赛4

9:00 T1 想法
10:00 放弃 T1 卡常工作
10:30 T2 读错题目
11:00 离开 T2
11:30 胡完 T3
T4 暴力并卡常 T1

期望：80+100+100+30，实际 80 + 100 + 25 + 30

---

T1 打表可以发现结论：

\(a_0 = c, a_1 = c^3, a_i = c^2a_{i - 1} - a_{i - 2}\)

这样，所有的 \(a_i, a_{i - 1}\) 构成一组解，并且可以构造出所有的解。

证明不会！

然后就好做了，比较愚蠢的做法是对于每一个询问单独做，枚举 c，在外面写一个矩阵快速幂“快速”地推 ai，这样就可以二分了。

当然，c 的枚举量不可以是 1e6，容易发现对于一个 c，a 的长度 >= 3 的不会太多，那么....

但是这样还是不可以的，还是很慢。

比较聪明的做法是把所有询问合起来做，暴力枚举 c 到 1e6，将 \([a_i, a_{i+1})\) 的询问答案 + i，这个可以用差分。

---

T2

sb 题，但是注意不要算重。

---

T3 巨大坑，但是确实也需要这样才能够对得住 T3 的位置。

很容易写出一个 DP，很容易猜测决策单调性，很容易写一个分治优化决策单调性，那么复杂度 \(O(nklog n)\)

看起来就过了！！

但是这样是假的，还需要考虑大区间的问题，定义大区间是至少包含了一个其他的区间的区间，小区间是没有包含任何其他区间的区间。

那么可以发现，对于一个大区间，要么和其对应的某一个小区间合并，此时视作不存在；要么单独分组。

证明：假如两个大区间合并，由于 \(|a\cap b| <= min(a, b)\)，所以肯定不如单个大区间一组，另外一个大区间并到其小区间里面。

那么，只需要把所有小区间单独提出来做前面的 DP，然后在最后讨论一下大区间占用的组数即可。

7.18

讲 昨天的 T4 给div3。

CF1610H Squid Game

首先可以讨论一条链/序列上的情况，发现 max dp[v] + 1 实际上等价于执行判断当前点是否需要新加点。

对于多个子树，讨论 max dp[v] + 1 成立的情况，注意所有依靠 w 的直链在其他子树里面已经选了点的时候已然被干掉了，发现依然正确。

这样的一个 DP 方程，不是依靠 DP 的定义直观地推导出来的，而更像是初始有一个讨论极其复杂的转移式，然后一步步简化得到，体现了 OI 的优美。

[USACO08OCT] Bovine Bones G：

虽然是普及题，但是有另外的理解方式。

设三个色子的概率生成函数分别是 \(F(x) = \sum p(i) x^{i}, G(x), H(x)\)

那么题目等价于求这三个生成函数的卷积所得到的系数的最大值的位置。

以这样的方式进行卷积：

计算 A * B，先将 B reverse，然后模仿滑动窗口，将先将 \(B^{\prime}\) 的最后一位（B 的第 1 位）和 A 的第一位对齐，将 \(B^{\prime}\) 和 A 重合的位置对应位相乘在相加，计算出 \([x^2](A * B)\)；然后将 \(B^{\prime}\) 平移一位，对应计算 \([x^3](A * B)\)

首先可以先让 F 和 G 卷起来，利用上面的对于卷积的理解方式，很容易知道结果形如一个 (k > 0)一次函数 + (y = c)一条线段 + (k < 0) 一次函数。

还需要再卷一个，讨论上述 线段 的长度和 H 长度的关系，利用对于卷积的理解方式，可以直接计算出在什么位置可以得到系数的最大值。

7.20 模拟赛5

8：10 快读读不了负号？？？

8：20 T2 结束，从未有如此美妙的开局

8：40 ？？？

9：10 尝试 T4

9：50 心态小裂

10：00 撤退 T3

感觉这把纯纯的罚坐。

T1 没开 long long，感觉已经好久没有犯这样的错误了，警钟敲烂。

---

T4：有趣的题目！！可以理解为一种 集合 HASH

只要找到某种二元操作，使得其不满足交换律，满足结合律，有逆元（有单位元），那么只需要给 0，1，2 分别赋值为三个随机值，只需要检查最后的答案的是否是单位元即可。

---

cin 跑的飞快的秘密。

讲 T3，意识到自己做题质量的问题，有点想当然了

二次剩余，勒让德

T4:https://www.fzoi.top/problem/7061

7.22 晚自习

ABC311

7.23 pb

QOJ 5571 Five letter warning 自己的做法，MLE，巧妙的熔池。取模！！！！！！！！！！！！！！！！！！！！！！！

CF1776C Library game： multiset vs set, 重载运算符，判定相同的方法是 < 不满足且 > 不满足，所以区间长度相同的会被认为一样，所以需要使用 multiset

n 组物品 (ai0, ai1, bi0, bi1) ，想要选 ai0 必须先选 ai1; bi0, bi1。Alice 和 Bob 轮流操作，目标都是差值最大。

我的贪心：

如果 ai0 > bi1，那么 B 不会主动拿 i；如果 bi0 >

n, m，给定 a1..n, b1...m，每次从原序列中抽出（删除）一个 a 的长度 m 的子序列，将这个子序列任意排列后，得到序列 p，将 max(p1 + b1, ..., pm + bm) 插回序列 a，保证最后剩下一个数，问剩下数的最小值。

7.24

探究 x -= ((mod - 1 - x) >> 31) & mod

n 个路灯，第 i 个可以选择照亮 [i - pi, i - 1] 或 [i + 1, i + pi] 之一，给出一个全覆盖的方案。

给定 li, ri 表示限制 ai\in[li, ri]，给定 c。求 \sum_i \sum_j cj [((a_i^a_{i - 1}) >> j) & 1] 最小值

[ARC119F]AtCoder Express 3

考虑对于一个没有问号的情况，如何求解最短路。显然不考虑最短路算法。

在逐渐往后走的过程中，可以发现我关心的字符数量是很少的，当碰到 BAAAAAB，那么一定会跳 B，之后，只会关心 AB....

那么，考虑将所有我关心的状态提出来，暴力建立状态之间的转移关系，也就是自动机。

• (B)A, (B)AA, (B)AAA, (B)AAA..A，指针在第一个 A。以及对应的相反的 4 个状态

如果在 (B)A 之后加一个 A，那么是容易的，如果加了一个 B，那么我肯定不会选择后退到 (B)，所以可以将 (B) 删掉，需要的新状态是 AB。

• AB，BA

(B)AA 之后 + B 是一样的，但是 (B)AAA 之后 + B 是不知所措的。

此时，要么花费 2 的代价，走到状态 AB；要么花费 2 的代价，走到状态 B。

注意到一个特殊点，状态 B 和状态 (A)B 是不同的，当前情况下，我走到 B 之后肯定不会使用 B 之前的 A。

对于 AB 而言，我可以钦定不使用 B。

新建立一个状态 O1，表示 A(B) / B。

(A)BBB 需要一个状态 O2 表示 B(A) / A，这两个状态看起来很可爱，看起来有合并的可能性。

我们需要考察这两个状态对于后续情况的判断是否一致：发现不管是 O1/O2，单独的 + A/B，他们都会暂时的按兵不动。

1. 增加 AA：对于 O1，ABAA/BAA，发现 BAA 肯定比 ABAA 厉害，新状态等价于 BAA...A，指针在 B；对于 O2，BAAA/AAA，BAAA 比 AAA 厉害，也会转移到 BAA...A
2. 增加 AB：对于 O1，ABAB/BAB，发现一定会使用 1 的代价，回到 O1；对于 O2，BAAB / AAB，使用 1 的代价走到 O1。

类似的分析，可以发现可以合并 O1, O2，叫做 O，表示 A/B，其实也就是最开始的状态

从上述的分析，发现看起来需要一个新状态叫做 BAA...A 指针在 B，和已有的状态 (B)AAA...A 很像。

warning：bug 点，这两个不是同一个状态/ll

简单思考，发现可以用 BAA...A 代替 (B)AAA...，然后将 (B)AAA 连到 (B)AAA... 的边改为连到 BAA...A，并增加 1 的代价。这样肯定是合法的，因为 (B)AAA... 一定是要先退到 B 的。

• OA, OB

还有一个思路是就硬用 (B)AAA，然后让 OA 连 边权 -1 的边

最后一个难点是 AB 状态 + A，分析发现连 O 就好了。

7.26

[NEERC2016] Mole Tunnels：设了一个 fij 表示 i 子树有 j 只没有解决，然后 j 可以为负。那么转移似乎就是 fij = \sum fls i + f rs j-i + w(i) + w(j - i)，然后 u 点的意义似乎就是给一个 dlt。

注意到每次新增一个鼹鼠，只会改变 dlt，而且树高 log，所以可以维护 dlt 随便做一做。

但是这样显然是错误的，因为贡献计算是失败的，比如，对于点 u 上的鼹鼠进入他的子树的情况，代价计算成了 1。为了避免这个情况，可以想到让洞移动的时候也会有代价，但是问题是最后的答案不方便计算。

所以还是应该老老实实模拟费用流。

HDU4718 The LCIS on the Tree：败走 reverse

[ABC311Ex]Many Illumination Plans：woc，我没有 DFS

7.27

线段树合并复杂度

zkw 线段树初探。

Call me Call me：本质是把一个矩形打成 log 个矩形。神仙分块做法

Splay 双旋原理

7.28

帮 zqm 调 LCT, rotate 的时候由于需要判断 isroot(f)，所以 fa[f] = x 一定要放到后面做。