Cayley-Hamilton 定理学习笔记
CH 定理主要用于优化线性递推。
下面很多东西都是自己瞎琢磨的,大概错漏挺多。
线代的一些基本知识
感觉学习 CH 困难的很大一部分原因就是缺少一些线代的基础。
- 矩阵的秩 ,说明向量组线性相关,说明行列式 。反之,如果 ,那么矩阵满秩。即二者充要。
证明:考虑行列式的性质即可,由于把第 行的线性组合加到第 行不影响行列式的计算结果,所以如果线性相关,那么说明可以把某一行全部消掉,那么自然不满秩。
- 对于一个 元齐次线性方程组 ,其中 是一个 的矩阵, 是一个由未知量构成的长度为 的列向量。其存在非全零解的条件是系数行列式
证明:当 时,矩阵满秩,感性理解一下,x 就只能是全零了。理性证明的话,考虑把 消成上三角矩阵之后,可以解出 ,进一步 也会解出是
- 特征值和特征向量
定义:
对于一个 阶方阵 ,若非 列向量 和 满足
那么称 为特征值 的特征向量
理解:
展开式子,有
若把矩阵的每一行理解为一个基向量 ,则是表示基向量与该向量的内积 等于
所以我们可以把矩阵 视作在 维空间中,对 在 个方向上进行不同程度的拉伸,这个拉伸的过程还可能伴随着旋转,因为如若把 视作基,即可以认为是掺杂了其他的基
而这个特征向量特殊的地方就在于,他真的就可以当做是基(即它是空间中的一些特殊的向量,使得 对这些向量施加变化的时候只有拉伸作用)
也就是说,矩阵 对应的 维空间的 个方向就是 个不同的特征向量所指的方向
此时,这个基构成 维空间 ,设 在空间 中的表示为 (投影??)
此时, 和 表示的完完全全的一个向量。只是说采用的基底不同
此时,我们计算 ,相当于对 在 的各个方向上进行了不同程度的拉伸变换(没有旋转了!)。程度的不同体现在 特征值 的不同,特征向量 对应的特征值 越大,那么 矩阵 在 所表示的方向上对 的拉伸作用越明显。
具体的,, 拉伸;, 不变;, 压缩
我们知道,向量是不能做除法的,但在特征方向上,就能除了,因为在两个向量共线时,它们所有的对应分量的比值都相同,而不共线时,比值就不同,就没法除了。
或参见:所有方阵都有特征值吗?如何证明? - 天下无难课的回答 - 知乎
- 矩阵 在复数集内有 个特征值。
证明:考虑特征值的定义,对于 ,它是通过一个特征向量来定义的,即二者大概是 1-1 对应,所以只需要证明有 个特征向量。
考虑 ,等价于 ,(这是我们熟知的特征多项式的形式)即证明它有 个解。
所以 ,这是上方已经证明的结论。
考虑这个行列式,它可以写成 为未知数的一元n次方程组,而 n次方程组在复数集内一共有n个解,(如果我们观察上式,可以发现 只出现在正对角线上,显然A的特征值就是方程组的解)同时,在对应 的条件下,可以解出 ,即特征向量。
这个结论说明了,上方所提到了 “这个基构成 维空间 ”,确实是一个 维度的空间。
同时这个其实可以看做是 CH 定理应用逻辑的一部分。
- 特征多项式
设 是一个 阶矩阵,则其特征多项式为 ,其中 是单位矩阵, 是一系列系数, 可以取很多种值,如其可以取为一个矩阵或一个数,注意当它取成一个矩阵的时候 也是一个矩阵
特征行列式和特征多项式其实指的是一个东西。
- 两个 阶多项式,如果有共同的 个零点,那么他们对应项的系数一定相同。
其重点在于,可能两个多项式的主元并不相同,但是系数可以一致。( 和 之类)
证明考虑回忆一下拉格朗日插值的原理之类之类。
- 特征根方程
在高中阶段,我们学习到这样一种求解线性递推数列的方法:
对于 阶线性递推数列 ,其特征根方程是
有这样一个结论,假如对于这个特征根方程有 个不同的解,即特征根 无重根。
首先 肯定是上述递推式的解。
其次,由于是线性递推,所以在不考虑初值的情况下,它的几个解的线性组合仍然是它的解。即通解是
然后,只需要带入 的初值,就可以得到 个方程,并解出 ,于是就能得到数列 的通项公式。
扩展:注意到这里是一定可以解出这 个方程的,因为这个关于 的方程的系数矩阵的行列式写出来是范德蒙德矩阵
这个技巧常常用于秒杀一类高中数列题
再扩展:假如有重根怎么办?留作思考/hsh
- 线性递推的转移矩阵的特征多项式就是特征根方程
(贺的官老师的)
假设一数列 满足 ,,转移矩阵 的特征多项式为 。
对于
设 表示取其最后 行 列的主子式的特征多项式
考虑计算行列式 ,如若第一行选择 ,那么有贡献
如若第一行选择 ,容易发现前 行选择的都是 ,最后一行会选择 ,此时逆序数 个
所以贡献为 ,即
考虑第一种贡献方式,有
所以, ,我们知道
而这个时候,如果我们对比一下 和我们的特征根方程,很容易发现他们是一样的!!!
那么进一步的,实际上,如果我们求出了特征多项式,那么我们实际上就获得了线性递推式。(这可能听起来有点鸡肋,我既然已经知道特征多项式,怎么会不知道原递推式呢?但是在下方的例题中展现出了威力)
Cayley-Hamilton定理
下面的等式在方阵 满秩时恒成立:
其中 是 的第 个特征值。
魔法地,注意到 和 的零点相同(),项数也相同,虽然说主元不一样,但是对应的多项式系数就是一样的。(上方基础知识里面讲过)
所以我们可以把上面的定理等价成为
加速矩阵快速幂
比如,我们要求 , 是一个 的矩阵,平凡的,我们的复杂度是 ,但是当 比较大的时候会被卡掉。这里有一种优化到 的方法
具体地,我们可以采用 这篇博客 中的方法先 求出 的特征多项式
由于 ,所以
设 , ,由于 ,所以
此时,我们完成了这样的一件事情:将矩阵的幂化成多项式的取模幂
即,设 ,将 带入,需要计算
所以,我们考虑平时做模意义下整数快速幂的方法,将整数乘法换成多项式乘法,整数取模换成多项式取模,就可以得到 ,这部分的复杂度是 暴力乘模 / NTT
最后需要带入 ,可以考虑直接 爆算,在齐次线性递推的背景下,就是初值的意思
加速线性递推
我们想要求出 ,
设这个转移矩阵 的特征多项式为 ,
设初值为列向量 ,第 行为 ,即求
根据上方讲过的知识,我们可以知道
求解出 之后,我们只需要求解 ,得到
回到原问题,我们求解的是 ,又有
好活,这样的话,我们一旦知道 那么就可以知道 ,若想要知道 这个列向量的所有值,我们也只需要知道
若只求单个元素,总时间复杂度是求 时的 。
若要求整个列向量,要么直接用 这个式子暴力矩阵乘法,时间复杂度 ,比直接矩阵快速幂少个 或者 ,且这样我们就只需要知道 ;
要么挨个元素去算,时间复杂度 。可以发现不用 和 取模的时间和普通矩快一样,用了的则是把 变成了
——gtr
多项式取模——听起来一个很奇怪的操作,凭啥会突然想到干这样一件事情呢?
考察我们如何求 ,
OI 的方法是,把转移矩阵搞出来,然后搞矩阵 次幂啥的。
小学的方法是暴力拆,例如对于 :
考察这个过程,其实就是每次找到等式中最大的一项,然后根据递推式把它变成更小的项。
上述过程,就是通过每次消去最高次项,求 对斐波那契数列的特征多项式 取模的结果的过程
特征多项式,也就是特征根方程,每次我们其实是将一个 代换为 ,其实也就是 减去 的若干倍,那么为了代换到底,这个若干倍要尽可能抵到顶,那么实际上做的就是取模。
即,「多项式取模」的过程恰好与「每次按递推式展开下标最大的那项」的过程一致,都可以用「替换」来解读。所以我们直接对 做多项式取模,就可以得到 这类形式。
例 1 「BZOJ4161」Shlw loves matrixI
模版题
#include <bits/stdc++.h>
using namespace std;
const int N = 4444;
const int mod = 1e9 + 7;
char buf[1 << 23], *p1 = buf, *p2 = buf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : * p1 ++)
int read() {
int s = 0, w = 1; char ch = getchar();
while(!isdigit(ch)) {
if(ch == '-') w = -1;
ch = getchar();
}
while(isdigit(ch)) {
s = s * 10 + (ch ^ 48),
ch = getchar();
}
return s * w;
}
void inc(int& a, int b) { a = a >= mod - b ? a - mod + b : a + b; }
void dec(int& a, int b) { a = a >= b ? a - b : a + mod - b; }
int add(int a, int b) { return a >= mod - b ? a - mod + b : a + b; }
int del(int a, int b) { return a >= b ? a - b : a + mod - b; }
int mul(int a, int b) { return 1ll * a * b % mod; }
struct vec {
int a[N];
void clear() {
memset(a, 0, sizeof(a));
}
}a, b, P, e;
int n, k, ans;
vec mul(vec a, vec b, vec P) {
vec ans; ans.clear();
for(int i = 0; i <= k; ++ i)
for(int j = 0; j <= k; ++ j)
inc(ans.a[i + j], mul(a.a[i], b.a[j]));
for(int i = k << 1; i >= k; -- i) if(ans.a[i])
for(int j = 0, tmp = ans.a[i]; j <= k; ++ j)
dec(ans.a[i - j], mul(tmp, P.a[k - j]));
return ans;
}
vec exp(vec a, int b, vec P) {
vec ans = e;
while(b) {
if(b & 1) ans = mul(ans, a, P);
a = mul(a, a, P), b >>= 1;
}
return ans;
}
signed main() {
e.a[0] = 1;
n = read(), k = read();
for(int i = 1; i <= k; ++ i)
a.a[i] = read(), P.a[k - i] = del(0, a.a[i]);
for(int i = 1; i <= k; ++ i)
b.a[i - 1] = (read() + mod) % mod;
P.a[k] = 1, a.clear(), a.a[1] = 1;
a = exp(a, n, P);
for(int i = 0; i < k; ++ i)
inc(ans, mul(b.a[i], a.a[i]));
printf("%d\n", ans);
return 0;
}
例 2 20240122 序列(sequence)
首先经过一通分析,可以得到这样的 DP 柿子:
初值 ,求
考虑这个咋做。
solution1(std):
如果将 这个向量看做一个整体,那么可以写出一个 的转移矩阵 (这也许可以叫做一阶线性递推把)
仔细观察转移式子,可以感性理解到对于每一个 而言, 是一个最高 阶线性递推序列(因为状态之间转移的时候没有对状态本身的平方,即类似 的项,所以都是线性关系)
考虑抽出 来看,而把其他都看成是辅助数组,即把 的位置都看成是由 中的某些项线性组合得到的东西。
那么,这个时候,我们的转移矩阵 也可以理解是, 本身的线性递推转移矩阵 经过非常复杂的线性变化得到的。注意到一个重要性质:特征多项式在基变更下不变。
那么,根据之前的结论,只需要求 的特征多项式(根据 Cayley-Hamilton 定理, 的特征多项式 ),就可以得到 的递推公式了。
非常厉害吧!
考察特征多项式:
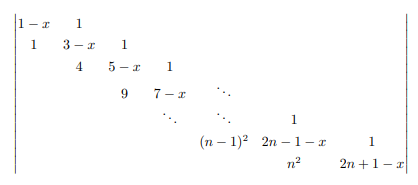
设 阶上述多项式是
若最后一行取右下角,那么
若最后一行取 ,那么倒数第二行只能取 ,有
所以有递推关系
其对应的递推矩阵:
设 ,那么
现在需要干的事情就是把 处理出来,其得到的结果矩阵 的第一行第一列就是我们要的特征多项式
为了避免多项式次数不平衡,这个的方法是考虑分治处理,复杂度
获得多项式 之后,可以直接套 取模的方法解决。但是为了复杂度,需要写一长串的多项式除法之类,非常麻烦,有一种小清新的算法是 波斯坦-茉莉算法。
solution2(jsy):
非常 powerful,注意到既然 是线性递推数列,且 其实都是 的一种线性组合。那么不妨尝试直接通过递推关系把 解出来。
知 ,由 DP 式子可以得到:
可以表达为 的样子。具体的,
那么进一步,将 带入 的式子里面,可以得到 和
代入的过程中肯定没有 和 相互的乘除,分子分母在代入下一个方程后会变成原来的分子分母的(类似)线性组合,肯定能拿矩阵来转移.(类似于树上主元法的时候的操作过程)
具体的:
把中间的矩阵和 solution1 一样分治乘起来,就可以通过 得到 。
那么这样就可以直接解 了,带进去会是一个求 的形式,其中 ,完美符合 波斯坦-茉莉 算法的要求,那么其实也可以通过 波-茉 的思路,把实际的递推式搞出来。
波斯坦-茉莉算法
正经的讲解 波斯坦-茉莉算法
时间关系,这里只记录一个关键的关系。
注意到对于给定一个线性递推 之后,对于 的构造是
和特征多项式/特征根方程进行对比,发现多项式 就是特征多项式。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具
2022-01-25 CF156D Clues 题解