2022 海亮集训总结

海亮集训总结

虽然这里标明了日期，但是很多消化的工作并不是在当天就完成的。可观的一部分内容在 8 月份完成。

写的比较详细，起因是有段时间做题太快了，有点根基不稳的感觉

内容大致包括比较详细的知识点梳理理解 和 简要/部分详细 的题解

题解以对如何想到解法的分析为主旨

7.07 树上问题

没听/qd，直接补，列表中有些题做过了

CF715C Digit Tree

naive：

一眼点分治然后考虑统计答案，考虑类似背包的方式跑两遍即可

容易想到可以把 \(10^{x}\) 除开，那么就是简单问题

但是被卡了 4h

主要 bug :
拿数字存在反着拿，然后不会了，给他上了个 map 回溯做，调了半天 T 飞了
点分治板子写错了/shuai

感觉是比较套路的点分治题目，评黑大概是因为是 CF 场上写出来需要一点码力

loj121 动态图连通性

naive：线段树分治 + 可撤销并查集板子

LCT：LCT 维护删除时间最大生成树

[SPOJ-QTREE6]Query on a tree VI

（以前做过）
开黑白两颗 LCT， LCT 维护子树信息

由乃的 OJ

容易想到线段树维护 l0, l1, r0, r1 表示从左/右边放一个 0/1， 出来是什么东西

然后得到了 \(O(nklog^2n), k = 64\) 的做法

上述四个变量都是 bool，发现实际没有必要开 \(k\) 棵线段树，\(k\) 位合在一起转移即可

[BZOJ4182]Shopping

看到树上问题应该有转化成序列问题的意识，通过 dfs 等树的遍历方式，树可以理解为序列问题的变式

—— wyb

可以想到固定一个必选点，暴力地，有 \(O(nm)\) 的树形依赖 DP

对于在树上做多重背包的题目，普通算法时间复杂度是O(nm2)。
此时我们可以考虑点分治。
一般的树上多重背包是从下往上更新，需要枚举转移量，因此效率低下。
经过点分治，转化为所有选择的点必须和重心连通，转化为从上往下更新。
每次向下递归时强制选择儿子，向上回溯时检查是否可以更新状态。
此时我们可以使用二进制拆分或单调队列对多重背包进行优化，将时间复杂度降为：O(nmlognlogd)或O(nmlog)

https://blog.bill.moe/DP-backpack-notes/

感觉点分治优化复杂度的原理在于分治，对于规模为 n 的问题，抽出一个关键点，处理必选关键点的情况，分治递归不选关键点。而这个关键点的选择显然与复杂度直接相关，结合算法可以看出每次应当选择重心。

具体有两种写法，一者对每一个分治中心求出 dfn, \(f_{i,j}\) 表示 dfn 后 i 个点，代价 \(j\)，好处是非常方便跳过子树

另一种设 \(f_{i, j}\) 表示点 \(i\) 的子树中，使用代价 \(j + before\) ，\(before\) 是到根的代价和，即强制选，实现非常精妙，大体秉承背包的思路，详见上面链接

bug: 在做单调队列优化多重背包的时候一定要小心后效性，即队列中的点的 \(f\) 应该保持是上层的值，不能说这次得到了新的 f 然后继续更新其他（否则导致选择了超过限制的物品数量）

[BZOJ4919]大根堆

2022.8.4 \([8：10,12：00] \cup [14:40, 15:20] \cup [15:40, 16:40]\)

虽然但是，下午很困，所以效率非常低下

非常有趣的思考过程！以下除特殊说明，都是自己的思考

最开始以为是通过树上主席树之类方式把能匹配的优化建图然后跑 DP 之类

思考了一下发现这个 DP 跑不动，因为匹配关系不能传递，而且子树之间是没有限制的，很难做

稍微转化一下题意发现是最大团的意思，但是边数还是太大了

那么换一个方向，发现链上的特殊情况就是 LIS，所以我们考虑把 LIS 扩展一下

设 \(f_{i, j}\) 表示 \(i\) 子树中，LIS 最后一位为 \(j\) 的答案

然后以为每次就是子树对应位相加 以及 \(f_{i, v_i} = \max\{f_{s, j < v_i}\} + 1\)

子树对应位相加是简单线段树合并，后面那个线段树上维护一下最大值随便搞搞即可

写出来发现不对。这样忽略了一个重要问题就是子树和子树直接是没有干扰的，也就是说有 \(f_{s1, j} += f_{s2, k < j}\)

然后不会了，跑去看 PPT，但实际上多想想应该是有希望的，就是改设 \(f_{i, j}\) 表示最后一位 \(\le j\)

重写

同样子树对应位相加，修改变成了让 \([v_i, m]\) 对 \(f_{i, v_i -1} + 1\) 取 \(\max\)

区间 \(\max\) 可以使用吉司机线段树，但是我就不。

PPT 给出的解法是注意到这个状态的单调性，然后 log^2 在线段树外面二分出 \(\max\) 最大影响范围。神似 两道料理 的处理方法

但是我觉得两个 log 有点不尽人意，询问了重复的区间 max,我要在线段树上二分

关于在线段树上二分的时间复杂度：

一般的，需要在每一个被询问区间包含的节点上再次往下走，所以是 log^2

如若在当前点就可以判断区间内是否有答案，那么只会在有答案的区间往下面走，且找到第一个答案就跑掉，log

线段树区间取 max 的方法：

一般的，我们使用吉司机线段树，维护最小和次小值，在不会有区间减之类的操作的时候均摊 log，证明类似颜色段均摊。在有区间减的情况下，吉司机线段树退化成为线段树上二分，log^2;

既然吉司机会退化成二分，我们考虑优化线段树上二分的做法，维护区间 min 和 max 和 tg，大于 max 直接 tg = 1 表示全部修改。

这样的好处是满足 “当前点就可以判断区间内是否有答案” 的条件，单 log

缺点是此时线段树不支持查询区间和，因为不知道一次的修改量到底是多少，这个只能交给两个 log 的吉司机了

所以这种与区间和有关的只能交给吉司机来做，比如 SNOI2020 区间和

本题中的线段树上二分：

同时注意到一个线段树合并的背景，考虑 merge 时，若 pushdown 发现左/右儿子不存在，那么此时实际上是不能够新开点的，不然 merge 复杂度就裂开了。但是实际上又是需要新开的，不然就会丢信息（tg 重置为 0）。

同时我们也有单点修改的操作需要 pushdown 下去。

所以，这里应当采用标记永久化的手法，tg 表示把区间对 tg 取 max

又要重写/ll/ll/ll

写的时候没有想清楚，最开始不知道在乱搞什么东西。。。

这样伴随的问题就是 mx,mn 的意义是区间实际最大/小值，所以 pushup 需要这样写:

void pushup(int rt) {
    t[rt].mx = max(t[rt].tg, max(t[ls(rt)].mx, t[rs(rt)].mx));
    t[rt].mn = max(t[rt].tg, min(t[ls(rt)].mn, t[rs(rt)].mn));
}

这样伴随的问题是由于线段树合并底层是加法而不是取 max，而 tg 永久化了又不能下传，所以需要在 merge 过程中把父亲的 tg 的影响计算出来得到真实值，大致意思是

pt = max(pt, t[p].tg), qt = max(qt, t[q].tg);
t[p].tg = t[q].tg = 0;

这样伴随的问题是不能 !p || !q 时立即 return ，因为这样没有把 pt 和 qt 的影响辐射到 p + q 里面

所以这个做法 G 了，维护区间max的标记的做法在这道题线段树合并的要求之下并不适用，GG

又要重写

另外一个视角看待，此处由于单调性，所以每次实际上是仅仅是区间加 1 ，发现维护区间加法标记非常好写，一发就过/hanx

解法2 ：

为了规避上述中存在的种种问题，可以直接维护 \(f[i][j]\) 表示长度为 j 需要的最小值。这样进行 DP ，就不存在什么区间 max，区间增加之类的问题了

这种解法也可以使用 multiset 做启发式合并

[HDU5290] Bombing plan

一眼树形 DP，想到设 \(f_{i, j, k}\) 表示向上可以冲 \(j\)，向下最深差 \(k\)

看了题解的状态，发现只有两维，思考了一下，发现如果这个点子树内差东西补不上，那么显然只能靠其他点来救。其他点能救那个叶子，自然可以救 \(i\)，所以此时 \(i\) 子树内没有选择点的必要性

所以可以直接设 \(f_{i, j}\) 表示向上冲 \(j\)，\(j = -1\) 表示 \(i\) 需要被救，\(j = -2\) 表示自己和儿子都需要救

如果我要选当前点，那么儿子肯定是尽量作死， \(\sum f_{v, -w[i]} \to f_{i, w_i}\)

如果我不选当前点，
\(j\ge 0\) 儿子很强，只要一个儿子强大就足够了， \(f_{v, j + 1} + \sum_{w ^ v} f_{w,-j} \to f_{i, j}\)
\(j < 0\) 儿子不能救，那就摆烂，\(f_{u, j} = \sum f_{v, j - 1}\)

最后一定记得对 \(f\) 做一遍后缀和

bug: 不能采用类似背包的转移方式，唯一矛盾在于 \(j\ge 0\) 不选当前点的时候需要知道其他所有儿子的和

Blue and Red Tree

番外：看到 Blue and Red Tree 应该想到向北方的 Red and Blue Tree

naive：简单手造小样例后发现是线段覆盖，可以使用二分图匹配，但是边数太多。

正解：观察连边特点，发现每次一定可以删掉的是只被覆盖过一次的边，而且如果不存在这样的边就 G 了

那么可以直接上一个树剖+线段树。一个问题在于需要取出覆盖某一个点的原线段，不优雅的方法是用 set 标记永久化，优雅的方法是维护线段编号的异或和，因为只被覆盖一次。

正解2：\bx ysy，思维独到，题目转化更进一步

可以发现每次选择一条边删除之后，分出了两个互不相关的连通块（ wyb 想到了这里但是没有继续了）

所以，条件可以转化为每次可以在红蓝两颗树上分别断掉一条边，使得分割开的两个连通块点集相同
（因为在红树上断开一条边之后两边也无关了，我居然想了好久）

那么，经典删边转加边，考虑最后一条被删除/第一条加入的边。

这条边必然既是红树上的边又是蓝树上的边，然后再递归地处理两边连通块即可。即如果发现有一条边既是红边又是蓝边，我们就将这条边连接的两个点进合并成一个点。如果最后能合并成 1 个点说明可行。

合并两个点的时候我们采用启发式合并来保证复杂度。具体来说维护每个点对应出去的边集的 multiset，然后逐个加入新边即可

实现的时候需要注意，由于合并了两个点 \((u,v)\)，那么清空了 \(v\) 的边集，可能 \((v, w)\) 本来是满足条件的，但是实际上合并的是 \((u, w)\)。

一种方式是并查集，另外一种是把 \((u, w)\) 加入队列然后取队首的时候判断一下

两种解法都是 \(\mathcal{O}(n\log^2 n)\)

7.10-7.11 容斥原理

Cyx 讲得非常精辟，可惜下午听课的时候由于中午没有睡觉导致头晕，掉麻了，是个损失

后续又没有机会能够再听一遍，列入 to-do list

学到了很多

Min_max 容斥

min_max 容斥的本质是容斥/jk

当然也可以通过二项式定理证明

高维前缀和

我们的高维前缀和实际上解决的是这样的问题：对于两个不同的组合对象，从对象 1 中选出 \(S\)

的方案数为 \(f(S)\) ，从对象 2 中选出 \(S\) 的方案书是 \(g(S)\) ，我们想要计算的是 \((f*g)(S)=\sum _{T_1\cup T_2 = S}f(T_1)g(T_2)\) 的值

发现实际上能产生贡献的 \((T_1,T_2)\) 需要满足如下条件：

• \(T_1\subseteq S,T_2 \subseteq S\)
• \(\forall x\in S , s.t. x\in T_1 \or x\in T_2\)

发现第一个条件是比较喜欢的，因为实际上它意味着所有在 \(T\) 中的元素都在 \(S\) 中，限制比较强烈

而第二个条件涉及到一个 \(or\) 的问题，比较麻烦，我们考虑把这个条件容斥掉

条件的否定是： \(\exist x\in S ,s.t. x\notin T_1 \and x\notin T_2\)

考虑枚举 \(S^{\prime }\) 使得 \(\exist x\in S^{\prime}\) 满足上述条件，考虑此时 \(T_1,T_2\) 满足的条件，有

\[\begin{align*} (f*g)(S)&=\sum_{S^{\prime}\in S} (-1)^{|S|-|S^{\prime}|}\sum f(\subseteq S^{\prime}) \sum g(\subseteq S^{\prime})\\ &= \sum_{T\in S} (-1)^{|S|-|T|}F(T)· G(T) \end{align*} \]

\(F(T),G(T)\) 就是高维前缀和

所以：并卷积 \((f*g)(S)=∑_{T_1∪T_2=S}f(T_1 )g(T_2 )\) 的高维前缀和为 \(F?G\)

即 \(f*g\) 为 \(F·G\) 的高维差分

怎么解释这个所谓“前缀和”的称谓？普通的，例如二维前缀和，实际上是二维偏序

在使用以素数为基的表示方法后，假设用 \(k\) 个素数表示出需要的数，那么此时就是一个 k 维偏序

考虑这样的高维前缀和的求法，大概有这样的代码：

for p\in prime
 for p|i
  f[i] += f[i/p]

复杂度变成埃筛的复杂度 \(O(n\log\log n)\)，也就是 P5495 Dirichlet 前缀和 的解法

抽象化一下：

已知 \(a_{p_1,p_2...p_k}\)，求所有 \(s_{p_1,p_2...p_k}=\sum a_{q_1,q_2...q_k}[q_i\leq p_i]\) ，也就是 \(k\) 维前缀和

最暴力的做法是直接枚举子集

对于 \(p_i\in {0,1}\) ，发现其实就是二进制的形式，妥妥的 FWT

仿照上面提到的做法：

初始化 \(s_{p_1,p_2...p_k}=a_{p_1,p_2...p_k}\) ，枚举 \(i\) ，考虑第 i 维的贡献

从小到大枚举 \(p_i\)，然后 \(s_{p_1,p_2,...p_i...p_k} += s_{p_1,p_2,...p_{i-1}...p_k}\)

时间复杂度为维数乘元素个数，和特殊情况的 FWT 相同

将每个数视为高维空间中的一个点，每个质数为一维，坐标为这个质因子的次数，这种时候一般称为 Dirichlet 前缀和

同理也可以求高维后缀和，高维前缀积等

二项式反演

\(g_n = \sum_{i =0}^ n \binom ni f_i \Leftrightarrow f_n = \sum_{i =0}^n (-1)^{n - i }\binom ni g_i\) 至多 n 个

\(g_n = \sum_{i = n}^ N \binom in f_i \Leftrightarrow f_n = \sum_{i = n}^N (-1)^{i -n}\binom in g_i\) 钦定 n 个

莫比乌斯变换与反演

mu 的构造思路：

莫比乌斯反演：

若 $g=1*f $ ，构造函数 \(\mu\) ，使得 \(1*\mu = \in\) ，有 \(f=\mu *g\)

写开：\(g(n)=\sum _{d|n} f(d)\)

考虑使用多元组来表示一个数，对于一个 \(n=\prod p_i^{a_i}\) ，我们使用 \((a_1,a_2,\dots ,a_r)\) 来表达

重定义 \(\subseteq\) 符号表示对于两个二元组 \((a_i) ,(b_i)\) ，若 \(\forall i, a_i\le b_i\) ，那么 \((a_i)\subseteq (b_i)\)

那么，可以表示成： \(g(S)=\sum _{T\in S} f(T)\) ，其实就是高维前缀和

所以对应的反演形式，也就是 \(f(n)=\sum_{d|n} \mu (\frac nd)g(d)\) ，可以看做是高维差分 \(f(S)=\sum_{T\subseteq S} (-1)^{|S|-|T|}g(T)\) ，而对应的 \(\mu(n/d)=(-1)^{|S|-|T|}\)

所以我们得以了解 \(\mu\) 的构造思路！

想象现在我们在做二维差分 ,\(a(i,j)=s(i,j)-s(i-1,j)-s(i,j-1)+s(i-1,j-1)\) ，系数都长成这样：

同理，考虑在刚刚所提到的表示法之下的系数，以 \(x=2^i 3^j\) 为例子

\(a(x)=s(x)-s(x/2)-s(x/3)+s(x/6)\) ，对应的 \(\mu(1)=1,\mu (2)=-1,\mu(6)=1,\mu(合数)=0\)

由此：

\[\begin{equation} \mu(N)= \left\{ \begin{array}{lr} 0,&\exist i\in[1,m],c_i>1\\ 1,&m\equiv 0(\bmod 2),\forall i\in[1,m],c_i=1\\ -1,&m\equiv 1(\bmod 2),\forall i\in[1,m],c_i=1\\ \end{array} \right. \end{equation} \]

当然，细心的同学们可以注意到一个问题，就是说实际上 \(\mu(n/d)\neq (-1)^{|S|-|T|}\) ，两者解决的问题有根本性的不同

后者为了解决并卷积的问题，使用了叫做高维前缀和的操作，而高维前缀和还需要配个系数以复原，把这个配的系数叫做与前缀和相对的高维差分，是凑出来的

而 \(\mu\) 更多的则是从差分的本身的意义出发，这里是从 2 维的计算方式扩展到这里在 \(\prod p_i^{c_i}\) 表示法之下的高维的计算方式

所以二者并不是相同的，一个显著的点就在于 \((-1)^x\) 取不到 0 ，也可以通过带入计算的方式，同样会发现两者的区别

（并不能仿照 \(\mu\) 在组合意义下的证明方式，利用 \(F\) 之间存在的关系，使得系数正负抵消为 0 的思路）
（只能说明是对这个玩意的理解太浅薄了）

求逆

平凡的，我们采用 NTT nlog n 求逆

在时间允许的情况下，我们可以把多项式卷积的形式看做一种特殊的莫比乌斯反演

如果 f=g?A ，求 A?B=1，则 g=f?B， 其中，B 可由 A ，n^2 推出

大概就是说 A*B = [i == 0] ，所以可以得到 B 的 x^{0} 的系数，继续带入即可

[CTS2019] 随机立方体 [solved]

二项式反演之后，从限制少的位置（较大值）开始考虑，发现是树的拓扑序模型

求n个点的树的拓扑序列的个数：

随机序列有 n! 种，我们考虑计算这么多方案书中成功的概率

对于以 i 为根的子树，要想让 i 排在所有子树中的点的前面，只有 \(\frac 1{siz_i}\) 的概率先抽到 i

所以答案就是 \(n! \prod \frac 1{siz_i}\)

[CF990G] GCD Counting [solved]

二项式反演后，只连结两端均为 k 的倍数的边，求得联通块大小即可

[FJOI2019] 新家具设计方案 [understanded]

没有提交地址

容易知道满足 \(y\in B \to y\le x\) 的最小 x ，可以使用插板法计算出 x 的方案数 \(f(x)\)

考虑 \(y\le x \to y\in B\) 的限制，设此限制下答案为 g(B) , 那么 f(x) 就是 g(B) 的带容斥系数的高维前缀和

所以做一个高维差分即可

[集训队作业 2018] 小Z的礼物 [solved]

覆盖所有 = E(max(S)) ，考虑 min-max 容斥 \(= \sum (-1)^{|t|+1} \frac{the\ count\ of\ black\ block}{f(T)}\) f(T) 表示能够覆盖任意一个 T 集合中的黑格子的不同骨牌数量

2^600 不可接受， 考虑计算相同 f(T) 的容斥系数和，即将 f(T) 相同的统一计算，由于同时选择相邻两个黑格子会影响方案数，考虑状压 DP

可以设轮廓线 dp(i,j,S,f) 表示轮廓线上的黑格子是否在 T 集合中， f(T)=f 的方案数

例题 [solved]

升级版：[UER #6] 逃跑

考虑期望线性性质，计算每一个点 (x,y) 在时间 t 第一次经过的概率 \(g[x][y][t]\)

容易 O(n^3) 递推出 $f[x][y][t] $ 表示（不管经过多少次）在时刻 t 刚刚好在 (x,y) 的概率

法1：发现我最后答案是 \sum\sum\sum g[i][x][y] ，所以考虑统一计算 \(G[i]=\sum\sum g[x][y][i]\)

容斥一下：\(G[i]=1-\sum G[j<i]f[0][0][i-j]\) 即到达一次后乱走回来

法2：\(f[x][y][i]=\sum g[x][y][j]f[0][0][i-j]\) 对多项式 \(f[0][0]\) 求逆 = h，那么 \(g[x][y]= f[x][y]*h\)

强调此处期望线性性的运用过程：本来是每一条路径的长度乘上出现概率，然后考虑枚举路径上每一个点出现的概率

对于升级版，方差的期望可以拆成 \(E(x^2)-E(x)\)

而 \(E(x^2)\) 可以理解为 \(2E(\binom x 2) + E(x)\) ，\(E(\binom x 2)\) 的意义就是在路径上选择有序点对的方案数的期望

暴力计算 \(E(\binom x2)\) 需要 \(n^4\) 枚举点对，不可接受，发现可以把相对位置相同的点对视作一个等价类一起计算，即设 \(h(i,x,y)\) 表示时刻 \(i\) ，经过了 \((a,b),(a+x,b+y)\) 的方案数（路径条数）的期望

计算出 h 即可

[AGC028D] Chords [Solved]

容易发现可以随便断掉环上一条边拉成链

发现连边条件是交叉，一个区间 [l,r] 会形成一个联通快

顺理成章，调换枚举顺序，计算一个区间 [l,r] 的出现次数，即 [l,r] 保证只向内部连边，保证 l,r 联通的方案数

这里不计算向外部连边的点且没有保证只有一个联通块，因为可以在其他的 [l^{\prime},r] 计算到，巧妙设计状态以避免算重

所以可以直接乘上 [1,l-1] 和 [r+1,n] 乱连的方案数，设 g[i] 表示 i 个点随意链接的方案数，当 i 为偶数时，\(g[i]=i!!\) ，否则 0

考虑计算 f[l,r] ，此处难以使用区间 DP 的转移方式，因为需要满足 l,r 的连通性，但是容易计算出不连通的方案数

即 “一个连通图不容易进行划分，而一个不连通的无向图则更容易划分成节点更少的部分”（蓝书 p337），

考虑枚举断点 k ，一种 naive 的想法是说 \(f[l,r] -= g[k-l+1] * g[r-k]\) ，即认为只要保证 l,r 不连通即可

仔细思考，发现这样实际上会算重，所以需要 “抓住一个点作为基本点”，我们考虑枚举 l 最远的联通的点 k ,贡献 -f[l,k]*g[r-k]

[AGC036F] Square Constriants [solved]

容易发现 p_i 的范围是两条以原点为中心的弧线，可以求出 \(p_i \in [l_i,r_i]\) ，注意到 \(\forall i\in [n+1,2n],l_i=0\) 考虑如果没有 l_i 的限制，那么按照 r 从小到大处理，答案就是 \(\prod r[i]+1-i\)

加入 l 的限制, 考虑容斥，naive 地，有 O（2^n 2nlog(2n) ），枚举哪些位置降阶 (r\to l)

观察答案的计算式，发现最重要的是 \(-i\) 的部分，即减去被选择的数量

发现计算被选择的数量 有可以整合的部分，考虑 DP

将 [1,2n] 升序排序， [1,n] 使用 l ，[n+1,2n] 使用 r

假设当前希求总共有 k 个数降阶，外层有容斥系数 (-1)^k

设 \(f[i][j]\) 表示当前前 i 个数，j 个数降阶的方案数，分类讨论即可

注意 j + (前i个数中只有r的数量) != i, 注意如若当前选择不降阶，那么所有降阶者都会影响

注意 p \in [0,2n-1] 大范围限制

[CF917D] Stranger Trees (hard version) [solved]

首先二项式反演 “恰好” \to “选取”/“至少，设为 g[k]

暴力枚举具体相同的 k 条边，形成 n – k 个联通块，将联通块缩点，计算生成树个数

知道两个点之间连边的方案数为 siz[u]siz[v]

考虑一个 Prufer 序列唯一对应一棵树，而点 i 在序列中出现 deg[i]-1 次

那么生成树个数为 \(\sum_{\sum deg=2n-2}\binom{n-2}{deg[1]-1,deg[2]-1,\dots,deg[n]-1} \prod siz^{deg-1}\) 注意这里的 n 其实指的是 n – k 个联通块

使用多元二项式定理，知道这个式子最终等于 \(n^{n-k-2}\sum\prod siz\)

问题变成计算$ \sum\prod siz$

Naive 地，设 \(f[u,i,j]\) 表示以 u 为根的子树有 i 个联通块，包含 u 的联通块大小为 j , O（n^3)

Trick ：各部分数量之积等于在每一部分选一个元素的方案数，即考虑组合意义

改设 f[u,I,0/1] 表示以 u 为根的子树中，I 个联通块，u 所在联通块是否选点的方案数，O（n^2)

[ZJOI2016] 小星星 [understanded]

原题，挺妙的，注意到之所以要记录 S 是因为考虑到是一个排列需要去重

所以直接容斥 S

[清华集训2014] 主旋律

神仙容斥题 Guess YCB 讲得很好

首先需要知道一个无环生成子图计数的套路

给出 \(n\) 个点的有向图，求有多少个无环生成子图
希求时间复杂度 \(O(3^n)\), 空间复杂度 \(O(2^n)\)

计数题考虑 DP，DP 状态设计的关键的在于对于阶段的划分，观察本题题目性质

无环生成子图的意思就是 DAG，DAG 显然是可以分层的，类比博弈论

所以，我们可以考虑每次提出出度为 \(0\) 的点进行计数。可以联想到 [AGC016F] Games on DAG

设 \(f_S\) 表示 \(S\) 集合的答案，容易想到暴力枚举集合 \(T\) 是当前所有 0 出度点， \(\sum_{T\subseteq S, T \not = null} 2^{e(T, S\backslash T)}f(S\backslash T)\)

但是问题是由于 \(T\) 到 \(S\backslash T\) 是随意连边，所以可能当前没有枚举到所有 0 出度点或者算重之类，需要容斥。

这里给出一种推容斥系数的方法，考虑对于一个大小为 \(k\) 的 \(S\)，在枚举 \(|T| = k - 1\) 的时候会被算 2 次， 在 \(|T| = x\) 时会被算 \(\binom kx\) 次

只希望算一次，所以 \(\sum_{j = 1}^k \binom k{j} coef_{j} = r_k = 1\)

二项式反演，\(coef_{k} = \sum_{j = 1}^k (-1)^{k - j}\binom kj r_j = (-1+1)^k - (-1)^k\binom k0 = (-1)^{k + 1}\)

所以：/tiao

\[f_S = \sum_{T\subseteq S, T \not = null} (-1)^{|T| + 1}2^{e(T, S\backslash T)}f_{S\backslash T} \]

回到本题，发现 scc 缩点之后就是 DAG

考虑设 \(f_S\) 表示 \(S\) 成为一整个 SCC 的方案，\(g_S\) 表示 \(S\) 成为若干个不连通的 \(SCC\) 的方案

类似的有 \(2^{e(S,S)} = \sum_{\varnothing\not = T \subseteq S} (-1)^{|T| + 1} g_T 2^{e(S\backslash T,T) + e(S\backslash T,S\backslash T)}\)

注意这里 \(f_S\) 当然不是 \(2^{e(S,S)}\)，为了方便，下面把所有 \(g_S\) 都乘上 \((-1)^{|S| + 1}\)，\(g_{null}=-1\)

稍微变化一下上面那个式子

\[g_S = 2^{e(S,S)} - \sum_{T\subsetneq S, T \not = null} g_T 2^{e(S\backslash T,T) + e(S\backslash T,S\backslash T)} \]

可以求出 \(g\)，考虑 f 和 g 的关系

\[g_S = \sum_{k}(-1)^{k + 1}\prod f_{s_1,s_2,\dots,s_k} \]

注意到，每加入一个 scc，容斥系数会乘上一个 −1。
由于是无序关系，所以我们可以枚举最小编号所在的强联通分量 T，然后就可以得到

\[g_S = - \sum_{T\subsetneq S, T\not =null} g_{S\backslash T}f_T \]

移项可以得到

\[f_S = g_S + \sum_{T\subsetneq S, T\not = nul} g_{S\backslash T} f_T \]

后续没有时间消化了

7.12-7.13 线性代数

上午听的时候非常想睡觉，想来是今天早上起得太晚了导致睡眠过量之类，所以上午的内容（行列式之前）G 了大半，但是依旧在努力听，努力思考，是值得肯定的，但是比较亏

下午听课状态不错，本以为上午听不懂是状态不好，下午发现原因其实是 太弱了+讲得真的是太好了

下午做题的时候有点走神，一段时间坐在那里大脑一片空白

感觉还是很有收获

将视频放入 to-do list

矩阵乘法

Cij 由 a 的第 I 行和 b 的第 j 列组成

for(int i = 1; i <= n; ++ i)
for(int k = 1; k <= n; ++ k)
for(int j = 1; j <= n; ++ j)
inc(res.a[i][j], a[i][k] * rhs.a[k][j] % mod);
//这样写常数更优秀，因为内存访问更友好

例题 [understanded]

给出一个随机数生成器（如右图所示）

T 组询问，每组询问给定种子和 n，询问第 n 次生成的值

T≤2×〖10〗^5, n≤〖10〗^18, 2s, 256MB

没有提交地址

将 seed 视作 64 维向量，在 F_2 域中，异或就是加法，位移可以通过乘上转移矩阵实现

设一次生成的转移矩阵 T ，T 是一个 64 \times 64 的矩阵，值只有 0/1

暴力复杂度 Q(64)^3\logn，采用前文中提到的常数更好的方法，发现可以压位，优化到一次询问 (64)^2\log n

不够，考虑预处理 \(T^{\lambda base^x}\) 其中 \(\lambda\in[1,base)\) ，预处理复杂度 base(64)^2\log n，此时一次询问复杂度 (64)^2\log_{base}n

由于向量乘矩阵的复杂度是 64，所以可以从向量开始乘起，那么一次询问的复杂度就是 (64)\log_{base}n

取 base = 256 即可

[NOI2020] 美食家 [solved]

经典拆点，经典 max+ 代替 +*，经典特殊贡献分段处理，经典预处理 T 的 2 的幂次方（

详见 wyb 的题解

[BZOJ3583] 城市路径问题 [solved]

容易发现可以 u\to v 的方案数就是 a_u * (b_v)^{T} ，所以容易将转移矩阵写成 (AB) 的形式

(T 表示转置)

套用 Matrix Power 的做法，可以处理 1+T+T^2+T3… 的问题

注意到 k 远远小于 n ，所以可以考虑 (BA) 成为一个整体，得到 k\times k 的转移矩阵，结束

[CF506E] Mr. Kitayuta's Gift [solved]

下面先处理 n+m 为偶

计数，考虑 DP

一般的字符串dp的套路：一位一位的放字符来进行决策

即枚举下一位放什么,这样dp有一个相当棒的好处就是我们永远不会重复数同一个串

考虑设 \(f(I,l,r)\) 表示在能够匹配原串的时候不会放着比配的前提下，处理了最终形成的串的前 I 个和后 I 个，原串剩下 [l,r] 没有处理的方案数

前提的意思是说，比如有一个 aab ，不能说加上一个 baabb ，因为这样会与 aabb 加上 b 算重

而这样的 DP 状态可以保证所有可以形成的串都可以被识别且不会算重，感性理解就是每次贴着边边走

这样，通过恰当的状态设计避免了算重的风险

转移：

\(S[l]==s[r] and r-l <= 1 ，25 * f[i][l][r] \to f[i+1][l][r]\)

\(S[l]==s[r] and r-1 > 1 , f[i][l][r] \to f[i+1][l+1][r-1]\)

? $ 25 * f[i][l][r] \to f[i+1][l][r]$

\(S[l]!=s[r] f[i][l][r] * 24 \to f[i+1][l][r]\)

? $ f[i][l][r] \to f[i+1][l+1][r]/f[i+1][l][r-1]$

将 (l,r) 视作一个点， \(\to\) 视作连系数（1,24,25）条边，发现形成一个 DAG，问题变成求有多少种方式可以走 \(ceil((n+m)/2)\) 步到达最终状态 $(l>r) $

这里连边实际上是方案数的意思，最终状态连 \(26\) 个自环

这里所谓的 DAG 实际上就是把本来不是非常清晰的 DP 转移过程刻画出来，使得我们可以更好地观察来优化

发现转移方式只和 s[l],s[r] 有关，可以对这个 \(m=strlen(s+1)\) ,m^4 大小的邻接矩阵强行快速幂，复杂度 $ m^6log$

观察信息冗余/寻找性质合并状态，发现我们并不关心具体是由那些状态到达，我们只关系路径上点的种类（24点，25点，26 点）的数量，顺序之类其都无关紧要

那么如果我们将经过点的点集相同的路径成为"一类路径"的话我们会发现两类路径的所包含的路径条数相等当且仅当这两条路径上自环数目为24,25,2624,25,26的点的个数分别相等(经过点集相同之后两个路径不同的唯一可能就是走自环方式不同了)

——Shadowice1984

发现想要走出一个 24 点需要匹配掉一个原字符，走出一个 25 点需要匹配掉两个

所以如若途径 x 个 24 点，那么就有 ceil((m-x)/2) 个 25 点

所以我们可以把经过 24 点的个数相同的状态数算出来一起处理，可以设 h[I,l,r] 表示从 [1,m] 走到 [l,r] 经过 I 个 24 点的方案数，m^3

此时，我们可以考虑把每一种链单独提出来做一遍矩阵快速幂，一共 o(m) 次，每次 m^3\logn

矩阵乘法兹瓷计算多个源点和汇点的路径方案数的，且此时顺序已经不重要了，我们考虑优化建图，把原本需要算 m 次的合起来算

我们发现刚才的算法之所以慢是因为你做了 \(O(|S|)\) 次矩阵乘法,问题来了你为什么要做矩乘呢？肯定是为了算从起点到终点的路径条数对不对啊,那么问题来了你刷出了一个 \(O(|S|^2)\) 的矩阵你却就提取这个矩阵的一位，剩下的中间变量又双叒叕被你扔了……算法当然会慢了

[1,m-1] 为 24 点，[m,m+ceil(m/2)) 为 25 点， m+ceil(m/2) 为终点

对于每一个 24 点，连边 m+ceil(x/2) ，边权 \(= \sum h(x,j,j)+\sum[s[j]==s[j+1]]h(x,j,j+1)\) ，连边 x,x+1 ,边权 1

对于每一个 25 点，连边 x, x+1 ，边权 1 ，让最后一个 25 点链接终点

最后处理奇数的问题，正难则反，发现奇数在上述算法中唯一不合法的贡献就是：

整条长为n+m的路径，恰好第n+m步是从[i,i+1]走到终点，所以只需要将终点的自环数量置为 0，且 24 点连边时，边权仅计算 \(\sum[s[j]==s[j+1]]h(x,j,j+1)\) 即可

O(m^3\log(n+m))

例题[understanded]

给定线性方程组 {█(w_11 x_1+w_12 x_2+?+w_1n x_n=a_1@w_21 x_1+w_22 x_2+?+w_2n x_n=a_2@?@w_n1 x_1+w_n2 x_2+?+w_nn x_n=a_n )┤

预先给定 (w_ij )

d 组询问，每组询问给出 (a_i )，求 (x_i )，答案对 p 取模，保证有唯一解

d≤1000, n≤100, p≤998244353

1s, 128MB

法1：如若允许离线，那么直接增广矩阵的右边增至 d 列

法2：LU 分解法，在对 w 做初等行变换的过程中记录一下行变换的逆 L ，直接对每一个 a 乘上 L 即可，或理解为计算一下初等行变换过程中 a 的系数变化

[LOJ6357] game [solved]

Play code myself

容易想到设 f[I,j,x] 表示当前有 I 个人活着，j 报数 x ，使得最终 1 号位存活的概率

转移的时候发现很不优雅，可以让编号统一 -1 ，并且直接去掉 x 那一维，直接改设 f[I,j] 表示 I 个人活着，当前报数 k 的人的 j

有转移：\(f[i][j] = 1/2 f[i][(j+k)\% i] + 1/2[j!=0]f[i-1][(j+k-1)\%(i-1)]\)

容易发现这样不断跳会形成环，需要高斯消元，一个长为 n 的环有 n 个式子，直接高消复杂度一次 n^3，GG，

观察系数矩阵，发现每一行都只有两个位置有值，即都可以写成 f_i[j] = k f[nex] + b 的形式，那主元法即可

注意细节

[CF963E]Circles of Waiting [solved]

听说是主元法，然后独立切出来了/hanx 总用时 3h 左右

暴力地想，可以把边界上所有点设为主元，但是发现这样没有必要，我只需要设最下面的点作为主元就可以了，然后可以根据对称性，在推到另外一边的时候得到等式，然后求解

所谓最下面的点就是 !check(I,j) and check(I – 1, j) 的点，check(x, y) 表示 (x,y) 出界

最开始没有考虑到还需要一个常数项，因为方程列错了，以为 f[I,j] =\sum f，但实际是 \sum f + 1，还需要走一步

写完之后，发现不对，检查出来犯了 个错误：

1.误以为有对称性，就是说 (r,0) 和 (-r，0）的期望应该是一样的，想的是根据这样的性质来列方程

\2. 没有把 (0,r) 和 (0,-r) 设成主元，因为延续 1 的想法考虑到列不出式子，误以为可以在不知道 (0,r)(0,-r) 的情况下推出 (1,r+1) 之类的点的式子，以为只需要特殊处理就好

\3. 输入的是 a_i ，不是 p_i ，p_i = a_i/{\sum a}

\4. 边界之外的点的 f = 0 ，而不是 1

\5. 判主元的条件写漏了 !check(I,j)

\6. 高消乱写/jk

把 r = 0 的时候特判掉了

改完之后还是不对，但是和我手模出来的过程都是符合的，GG

上个厕所冷静了一下，发现 (0,r）(0,-r) 必须设出来，发现有 2r 个未知数但只有 2r-2 个方程

吃个饭冷静了一下，发现没有对称性，思考出了列方程的正确方式，好耶

最后一个 bug：等式移项请变号

nice

线性空间

从 n 维行/列向量抽象而来，在集合 V 上定义加法和数乘运算

满足以下定律的称为线性空间：

• 加法有交换律、结合律，存在零元素 0、负元素 -α
• 数乘有结合律，1?α=α
• 加法与数乘有分配律

V 的每个元素仍称为向量

线性相关

一个向量能被集合中其他向量表示出来

基、坐标、维数

把基看做是坐标轴，那么坐标就是坐标（/qd

线性映射的矩阵

在基 \beta 之下， v_i 的坐标为 \(a_{ij}\)；在基 \(\gamma\) 之下，v_i 的坐标为 a^{\prime}_{ij}

那么 a * A = a^{\prime}，即， \([A]_{\beta}^{\gamma}\) 就是把 \beta 意义下的坐标转化为 \gama 意义下的坐标

所以线性映射就是矩阵乘列向量: \([A(v)]_{\gamma} = [A]^{\gamma}_{\beta} [v]_{\beta}\)

基的变换 & 秩

掉线

[Yahoo Programming Contest 2019 E +] Odd Subrectangles +[solved]

并没有按照 ppt 上面的解释且没有懂 ppt 上的解释

假装现在我们已经固定了行的选法，设有 a 个列和为奇数， b 个和为偶

这样类似的思路（先确定行）的题有：CF662C Binary Table

那么从 a 中挑一个控制奇偶性，偶列可以随便选，方案数 2^{a+b-1} = 2^{m-1}

考虑计算 a > 0 的方案数，发现直接计算非常困难，不能对每一列单独考虑

正难则反，考虑计算全是偶数的方案数，有这样的思考：先随便选一些行，然后找到另外的一些行使得行的异或和（将一行视作一个 bitset）为 0

之所以是异或，是因为我们此处是在 F_2 域下考虑这个问题

知道这样的方案数是 2^{n - rank} ，因为线性基外的数都可以通过线性基内的数拼凑出来

答案就是 (2^n – 2^{n – rank}) * 2^{m – 1}

后续没有时间消化了

7.14 线性递推和多项式

事实说明听不懂确实不主要是状态的问题，本身讲解的难度占了大部分原因

上午听到后面直接大脑放空了，感觉完全超出了接受的范围，经过长时间的强行接受（这里听不懂，先假设这个就是正确的，接着听）和自主拼凑细节推导，人麻了

下午努力地在理解什么叫做特征值以及他的意义，花了很多时间，理解之后感觉不理解为什么之前会不理解

czl 问了我关于 \(\mu\) 和高维前缀和关系的问题，没有回答得上来，花了 1h 左右，理解之后感觉不理解为什么之前会不理解（只能说是对于高维前缀和到底是干什么的差点理解/qd

具体的补充到 7.10-7.12 的总结中了

感觉很有必要在把所有东西都消化完之后重看一遍所有视频，应该会有更深入理解

特征值和特征向量

定义：

对于一个 \(n\) 阶方阵 \(A\) ，若非 \(0\) 列向量 \(\vec{v}\) 和 \(\lambda \in \C\) 满足 \(A\vec{v} = \lambda\vec{v}\)

那么称 \(\vec{v}\) 为特征值 \(\lambda\) 的特征向量

理解：

展开式子，有

若把矩阵的每一行理解为一个基向量 \(\varepsilon_i\)，则是表示基向量与该向量的内积 \((\varepsilon_i \cdot \vec{v})\)等于 \(\lambda \vec{v}\)

所以我们可以把矩阵 \(A\) 视作在 \(n\) 维空间中，对 \(\vec{v}\) 在 \(n\) 个方向上进行不同程度的拉伸，这个拉伸的过程还可能伴随着旋转，因为如若把 \(\vec{v}\) 视作基，即可以认为是掺杂了其他的基

而这个特征向量特殊的地方就在于，他真的就可以当做是基

也就是说，矩阵 \(A\) 对应的 \(n\) 维空间的 \(n\) 个方向就是 \(n\) 个不同的特征向量所指的方向

此时，这个基构成 \(n\) 维空间 \(S\) ，设 \(\vec{v}\) 在空间 \(S\) 中的表示为 \(\vec{a}\) （投影？？）

此时，\(\vec v\) 和 \(\vec a\) 表示的完完全全的一个向量。只是说采用的基底不同

此时，我们计算 \(A \vec a\) ，相当于对 \(\vec a\) 在 \(S\) 的各个方向上进行了不同程度的拉伸变换（没有旋转了！）。程度的不同体现在 特征值 的不同，特征向量 \(\vec v\) 对应的特征值 \(λ\) 越大，那么 矩阵 \(A\) 在 \(\vec v\) 所表示的方向上对 \(\vec a\) 的拉伸作用越明显。

具体的，\(λ > 1\), 拉伸；\(λ = 1\), 不变；\(λ < 1\), 压缩

注意到这个特征值是固定的

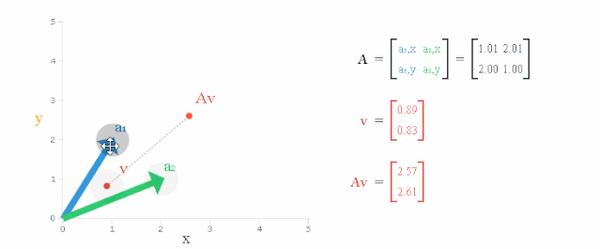
（图源：如何理解矩阵特征值的意义? - 知乎 (zhihu.com)）

特征值的作用：

找到一组基，使得线性变换在这组基下的矩阵为对角矩阵。

也就是所谓的对角化 （这部分内容有助于哈密顿-凯莱定理的证明）

对角矩阵：只有主对角线上有值的矩阵

对角化：对于一个 \(n\) 阶矩阵 \(M\) ，找到一个矩阵 \(A\) ，使得 \(A^{-1}MA\) 为对角矩阵

定理：任意一个 \(n\) 阶矩阵如果存在 \(n\) 个线性不相关的特征向量，则该矩阵可被对角化

证明：设 \(M\) 的 \(n\) 个特征值为 \(\lambda_i\) ，\(\vec{v}_i\) ，我们说 \(A = [\vec v_i]\)

注意此处 \(A\) 是 \(n\) 阶矩阵，每一列都是一个 \(n\times 1\) 的特征向量

那么 \(MA = M[\vec v_i] = \lambda {\vec v_i}\)，展开式子：

\[\left[ \begin{array}{ccc} \vec v_1 & \vec v_2 & \cdots & v_n \end{array} \right] \left[\begin{array}{ccc} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots &\lambda_n \end{array} \right] \\ = A\left[\begin{array}{ccc} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots &\lambda_n \end{array} \right] \]

左边再乘上一个 \(A^{-1}\) ，所以

\[A^{-1}MA =\left[\begin{array}{ccc} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots &\lambda_n \end{array} \right] \]

也就是说，一个 \(n\) 阶矩阵，对角化之后就得到了一个主对角线上全是 \(\lambda\) 的对角矩阵

这样的对角矩阵可以记作 \(diag(\lambda_1,\lambda_2,\cdots , \lambda_n)\)

当然也可以证明 \(A\) 是为唯一的，所以这个定理是充要的

那对角化又有啥用呢？

例子（来源)若一个可对角化的矩阵 \(M\)，求 \(M^{1e9}\)

先对角化一下，设 \(S = A^{-1}M A\) ，\(A\) 是由 \(M\) 的特征向量组成的矩阵

那么 \(M=ASA^{-1}\) ，\(M^2 = ASA^{-1}ASA^{-1}=AS^2A^{-1}\)

所以 \(M^{1e9} = AS^{1e9}A^{-1}\)，对角矩阵的次幂自然是容易计算的

（呼，终于走出了第一页 ppt ，而 cyx 只用了 1 分钟/jk）

特征多项式

\(Ax ?=λx ?\) 可以写成 \((λI_n-A) x ?=0 ?\) 这是一个关于 $x ? $ 的齐次线性方程组

它有非零解的充要条件是 \(|λI_n-A|=0\)，称为特征方程

关于 \(λ\) 的函数 \(|λI_n-A|\) 是一个 \(n\) 次多项式，称为 \(A\) 的特征多项式

特征值就是特征多项式的根，在复数域上一定有 \(n\) 个根（重根计算在内）

相似矩阵的特征多项式相同

（上面五行直接贺的 ppt ）

相似矩阵（文章重点大致在文末） ，相似矩阵的作用和特征值的作用比较相似

$n $ 阶矩阵 \(A\) 相似于对角矩阵的充要条件是 \(A\) 有 \(n\) 个线性无关的特征向量

同时，特征多项式相等，特征值就一定相等，因为特征值是特征多项式的根 [具体解释](为什么特征多项式相等，特征值就一定相等？_百度知道 (baidu.com))

矩阵特征多项式的求法

多项式可以差值，特征多项式是一个 \(n\) 次多项式，所以我们需要 \(n + 1\) 个点值，对每一个点值求值的过程中，考虑到特征多项式本来是个行列式，所以我们只需要采用行列式的高斯消元的方法，总共是\(O(n^4)\)

有通过构造相似上海森堡矩阵使这一步加速到 O(k3) 的方法，但是我不会。这篇博客里面有讲

哈密尔顿-凯莱定理

设 A 的特征多项式为 \(f(λ)=|\lambda I_n-A|\)，则 \(f(A)=O\)

哈密顿-凯莱定理为什么不用矩阵或线性变换直接代入？ 大意是说带入 \(\lambda E\) 之后，仍然是数乘，也就是 \(A \cdot E\) 而不是矩阵乘法，所以实际上是一个分块矩阵，即 \(diag(A,A,\dots ,A)\)

哈密尔顿-凯莱定理的证明 大意是说要利用对角化之后的性质，将计算 \(\lambda I_n -A\) 的行列式转换为计算 \(C=[\vec {v_i}]\) 的行列式（\(\vec{v}\) 是特征向量），\(|C|\) 的计算是可以直接展开的（对角矩阵），这样就把 \(\lambda E\) 消成 \(\lambda\) ，在把 \(A\) 当做 \(\lambda\) 带入，然后就可以证了。

加速矩阵快速幂

在网上转了一圈发现还是 cxy 的 ppt 做得最清晰（但是好像讲得。。。

比如，我们要求 \(M ^n\) ，\(M\) 是一个 \(k\times k\) 的矩阵，平凡的，我们的复杂度是 \(k^3\log n\) ，但是当 \(k\) 比较大的时候会被卡掉。这里有一种优化到 \(O(k^3)-O(k\log k\log n)\) 的方法

具体地，我们可以采用 这篇博客 中的方法先 \(O(k^3)\) 求出 \(M\) 的特征多项式 \(f(\lambda) =|\lambda E-M|\)

由于 \(f(M) = 0\) ，所以 \(M^n = M^n \bmod {f(M)}\)

设 \(g(x) = x^n\) ， \(g(x) = h(x)f(x)+r(x)\) ，由于 \(f(x)=0\)，所以 \(g(x) = r(x)\)

此时，我们完成了这样的一件事情：将矩阵的幂化成多项式的取模幂

即，设 \(\lambda ^n \bmod f(\lambda) = \sum _{i = 0}^{k - 1} a_i \lambda^{i}\) ，将 \(\lambda = M\) 带入，需要计算 \(\sum_{i = 0}^{k - 1}a_i M^{i}\)

所以，我们考虑平时做模意义下整数快速幂的方法，将整数乘法换成多项式乘法，整数取模换成多项式取模，就可以得到 \(a_i\) ，这部分的复杂度是 暴力乘模 \(O(k^2 log n)\) / NTT \(O(k\log k\log n)\)

最后需要带入 \(M^{i = 0\dots k -1}\) ，可以考虑直接 \(O(k^4)\) 爆算，在齐次线性递推的背景下，就是初值的意思

线性递推

贺一个定义：

\(k\) 阶线性递推数列 \({f_n}\) 指的是：

\[f_i=\begin{cases} r_i,&i<k\\ ∑_{i=1}^kf_{n-i}q_i ,&i≥k \end{cases} \]

其中 \(r_0, r_1,…, r_{k - 1};q_1, q_2, …, q_{k - 1 }\) 是常数

线性递推数列可以写成矩阵形式

\[\begin{bmatrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ q_k & q_{k - 1} & q_{k - 2} & \dots & q_1 \end{bmatrix} \begin{bmatrix} f_{n - k}\\f_{n - k + 1}\\\vdots\\f_{n - 2}\\f_{n - 1} \end{bmatrix} = \]

\begin{bmatrix}
f_{n - k + 1}\f_{n - k + 2}\\vdots\f_{n - 1}\f_{n}
\end{bmatrix}

\[ \]

注意 \(q\) 在矩阵中的下标是反正来的，因为这里是一个类似卷积的定义方式

例题有：排队 - 题目 - FZUOJ (fzoi.top) 预处理 \(r\) ，矩阵乘法每次只新增 \(f_n\) ，其他部分直接平移

（以下大部分参照 orzgtr)

类似地，仿照前面特征多项式加速矩阵快速幂的方式，我们可以加速齐次线性递推，毕竟线性递推数列可以写成转移矩阵的形式

我们想要求出 \(h_n (n\ge k)\) ，\(h_n = \sum_{i = 1}^ k a_i h_{n - i}\)

设这个转移矩阵 \(M\) 的特征多项式为 $f(\lambda) $ ，\(g(\lambda) = \lambda^n\)

设初值为列向量 $B $ ，第 \(i\) 行为 \(h_{i - 1}\) ，即求 \(BM^n[0]\)

我们考虑求出 \(f(\lambda)\) ，此时，假装 \(O(k^3)\) 的复杂度无法满足我们的需求，我们探究一下 \(f(\lambda)\)

\[|\lambda E - M| = \left|\begin{bmatrix} \lambda & -1 & 0 & \cdots & 0 \\ 0 & \lambda & -1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & -1 \\ -a_k & -a_{k - 1} & -a_{k - 2} & \dots & \lambda-a_1 \end{bmatrix}\right| \]

设 \(F_k(x) = \sum _{i = 0}^k c_{k,i} x^i\) 表示取其最后 \(k\) 行 \(k\) 列的主子式的特征多项式

考虑计算行列式 ，如若第一行选择 \(\lambda\) ，那么有贡献 \(\lambda F_{k - 1}(\lambda)\)

如若第一行选择 \(-1\) ，容易发现前 \(k-1\) 行选择的都是 \(-1\) ，最后一行会选择 \(-a_k\) ，此时逆序数 \({k-1}\) 个

所以贡献为 \((-1)^{k-1} · - a_k (-1)^{k-1}=-a_k\)，即 \(c_{k,0} = -a_k\)

考虑第一种贡献方式，有 \(c_{k,i} = c_{k-1,i-1} = \dots = c_{k-i,0} = -a_{k-i}\)

所以，\(F_k(x) = x^k - \sum _{i =0}^{k-1}a_{k-i}x^i\) ，我们知道 \(F_k(x) =f(x)\)

求解出 \(f\) 之后，我们只需要求解 \(g(x) \bmod f(x)\) ，得到 \(\sum n_i x^i\)

回到原问题，我们求解的是 \(BM^n[0] = \sum_{i = 0}^{k-1} n_iBM^i[0]\) ，又有 \(BM^{i}[0]=h_i (i<k)\)

好活，这样的话，我们一旦知道 \(h_{0\dots k-1}\) 那么就可以知道 \(BM^n[0]\) ，若想要知道 \(BM\) 这个列向量的所有值，我们也只需要知道 \(h_{0\dots 2k-1}\)

若只求单个元素，总时间复杂度是求 \(M^n\) 时的 \(O(k^2logn)/O(klogklogn)\)。

若要求整个列向量，要么直接用 \(∑_{i=0}^{k^1}n_iBM^i\) 这个式子暴力矩阵乘法，时间复杂度 \(O(k^2\log n+k^3)\)，比直接矩阵快速幂少个 \(\log\) 或者 \(k\)，且这样我们就只需要知道 \(h_0,h_1,\dots,h_{k?1}\)；

要么挨个元素去算，时间复杂度 \(O(k^3logn)/O(k^2logklogn)\)。可以发现不用 \(NTT\) 和 \(k \log k\) 取模的时间和普通矩快一样，用了的则是把 \(k\) 变成了 \(\log k\)

——gtr

模板

BM 算法

这把 sb 了，对着一个 \(O(n^2)\) 的多项式取模看半天没看懂什么意思，简单 yy 了一个大除法的过程发现就是模拟。。。

然后好像对于线性递推的定义有两种？导致最开始不知道的时候根本无法理解另外一种定义下的推导方式

感觉大致明白之后不是很理解为什么之前会看这么久看不懂/qd，大概是基础太差了

通过：浅谈 BM 算法 GTR cz_xuyixuan & cyx 的ppt 学习 ，cyx 的 ppt 有强大的提纲挈领的作用

Berlekamp-Massey 算法是一种用于求数列的最短递推式的算法。给定一个长为 \(n\) 的数列，如果它的最短递推式的阶数为 \(m\)，则 Berlekamp-Massey 算法能够在 \(O(nm)\) 时间内求出数列的每个前缀的最短递推式。最坏情况下 \(m = O(n)\)，因此算法的最坏复杂度为 \(O(n ^ 2)\)。

——OI Wiki

定义

数列 \(\{a_0\dots a_{n - 1}\}\) 的递推式 \(\{r_0\dots r_m\}\) 满足：

\[\sum_{j = 0} ^ m r_j a_{i - j} = 0, \forall i \ge m \]

其中， \(r_0 = 1\) ， \(l_i = m\) 为该递推式的阶数

注意这里和前述的线性递推的定义有细微差异，大概是加一个负号的意思

引理

如果 \(r_{i - 1}\) 不是 \(a_i\) 的递推式，那么 \(l_i \ge \max(l_{i - 1}, i + 1 - l_{i - 1})\)

\(l_i\) 显然 \(\ge l_{l - 1}\)

反证法，考虑如若 $l_i < i + 1 - l_{i - 1} $ ，我们现在只需要证明 \(r_{i - 1}\) 依然是 \(a_i\) 的递推式

下称 \(r_{i_1}\) 为 \(p\) ， \(r_{i}\) 为 \(q\)

\[\begin{align*} a_i &= -\sum_{j = 0}^{l_{i-1}} p_j a_{i - j} \\ &= \sum_{j = 0}^{l_{i-1}} p_j \sum_{k = 0}^{l_i} q_k a_{i - j - k} \\ &= -\sum_{k = 0}^{l_i} q_k a_{i - k} \end{align*} \]

注意第二个等号的成立条件就是 $l_i < i + 1 - l_{i - 1} $，简单验证，当 \(j = l_{i -1} , k = l_i\) 的时候，\(i - j - k = 0\)

第一/三个等号的符号是因为定义的原因。此时，第一/三个等号的意义分别为 \(a_i\) 可以被 \(r_{i - 1}/r_i\) 表示

推论：对于 \(n\) 阶线性递推数列，最短递推式就是其前 \(2n\) 项的最短递推式

因为 \(l_{2n} = max(l_{2n - 1}, 2n + 1 - l_{2n-1}) = n\)

求解

知道答案下界，考虑构造到这个下界。这也是做题中一种经典的思考，先思考答案的下界然后考虑构造

引理中的式子提醒我们使用增量法，初始令 \(r_0 = 1\) ，即 \(a_i\) 前系数为 \(\rm 1\)

假设当前已知 \(r_{i - 1}\) ，如若 \(r_{i - 1}\) 适用于 \(a_i\) ，直接 \(r_i = r_{i - 1}\)

考虑不适用的情况，以生成函数视角看待这个问题，设 \(A\) 是 \(a\) 的生成函数， \(R_i\) 是 \(r_i\) 的生成函数

那么有 \(AR_{i-1} \equiv S_{i - 1} \pmod{x^{i}}\) ，这里 \(S\) 大概是 \(-A\) 的意思

此时，由于 \(r_{i-1}\) 不适用，所以 \(AR_{i-1} \equiv S_{i - 1} + cx^{i} \pmod{x^{i+1}} \qquad (1)\)

考虑上次在 \(p-1 \to p\) 的过程中也出现了不适用的情况，我们考虑在上次调整的基础上在进行调整

设 \(AR_{p -1} \equiv S_{p - 1} + dx^{p} \pmod {x^{p + 1}}\)

两边同乘 \(x^{i-p}cd^{-1}\) ：\(AR_{p - 1} cd^{-1}x^{i-p} \equiv S_{p - 1} cd^{-1}x^{i-p} + cx^{i} \pmod {x^{i + 1}}\qquad (2)\)

（。。。为什么最开始会以为不用乘 \(x^{i-p}\) 啊，模数不统一怎么做减法啊）

\((1) - (2):\) \(A(R_{i - 1}-R_{p - 1} cd^{-1}x^{i-p}) \equiv S_{i - 1} - S_{p - 1} cd^{-1}x^{i-p} \pmod{x^{i + 1}}\)

很明了了， \(R_i = R_{i - 1}-R_{p - 1} cd^{-1}x^{i-p}, S_i = S_{i - 1} - S_{p - 1} cd^{-1}x^{i-p}\)

我们可以验证一下，\(R_{p-1}\) 有 \(l_{p - 1}\) 阶，乘上 \(x^{i - p}\) 就是 \(i - p + l_{p - 1}\)

由于 \(p-1\) 是最近的一次上次修改的时候，所以 \(\forall j\in[p, i - 1] ,l_j = p + 1 -l_{p - 1}\)

所以 \(l_i = i - p + l_{p - 1} = i - p + (p + 1 - l_{i - 1}) = i + 1 - l_{i - 1}\)

nice

优化一类 dp

假设一类 \(dp\) 可以用矩阵快速幂计算（即形如 \(dp_{i,j}=∑dp_{i−1,k}⋅f_{k,j}\)），最后要求 \(∑k_idp_{n,i}\) 或其他类似的东西，有一种万能的办法：把它的前 \(2k\) 项扔进 BM 算出它的递推式，然后直接 \(k^2\log⁡n\) 或者 \(klog⁡klog⁡n\) 计算即可。因为矩阵是有最小多项式的，所以这个 \(dp\) 本质上也是一个线性递推，由 B 的最小多项式定义，所以其递推项数不超过 k。

也就是说，计算 \(v,vB,\dots ,vB^{2k}\) 的递推式，然后利用前面所述 哈密尔顿-凯莱定理 加速线性递推的方法求解

Expected Value Flying2018

插值

常用拉格朗日插值

牛顿插值可以 点值表示 \(\to\) 下降幂表示，但是不懂

插值的一个经典应用是自然数幂和

加强一下就是 [BZOJ3453] XLkxc[solved] ，一层套一层乱插即可

再加强一下：[CF933E]A Creative Cutout[understaned] 推式子推成可以拉插的形式

或者 [NOI2019]斗主地[confused]

下降幂多项式与斯特林数

$n^{\underline m} = m! \binom nm $

第一类斯特林数

无符号： \(s_u(n, m)\) 表示将 \(n\) 个球分成 \(m\) 个非空圆排列的方案数，可以记作 \(n\brack m\)

有符号： \(s_s(n, m) = (-1)^m s_u(n, m)\)

递推公式： \(n\brack m\) \(=\) \({n - 1}\brack {m - 1}\) \(+(n - 1) \times\) \({n - 1}\brack{m}\) ，随便 yy 可以证明

下降幂多项式转幂多项式：\(x^{\underline n} = \sum_{i = 0}^n s_s(n, i) x^i\)

证明：归纳法， \(x^{\underline n} = x^{\underline{n - 1}}(x - n + 1) = \sum_{i = 0}^{n - 1} s_s(n - 1, i)x^{i + 1} - (n - 1)\sum_{i = 0}^{n - 1}s_s(n - i,1)x^i\)

观察这个式子，把 \(x^m\) 的系数提取出来，发现符合 \(s_s\) 的定义式，即 \(s_s(n, m) = s_s(n - 1, m - 1) - (n-1)\times s_s(n - 1, m)\)

上升幂多项式转幂多项式：\(x^{\overline n} = \sum_{i = 0}^n s_u(n, i) x^i\)

证明：归纳法，考虑 \(x^{\overline n} = x(x + 1)(x + 2)\dots(x + n - 1)\)， 我们需要证明其 \(x^m\) 项的系数为 \(n\brack m\)

• 如果最后一个括号里面选了 \(x\)， 那么前面需要选 \({n - 1}\brack {m - 1}\)
• 如果最后一个括号里面选了 \(n - 1\)， 那么前面需要选 \(m\) 个 \(x\)， 所以 \(x^m\) 的系数是 \((n - 1)\times\) \({n-1}\brack{m}\)

我的评价是：这种好事

第二类斯特林数

\(S(n, m)\) 表示 \(n\) 个球分成 \(m\) 个非空集合的方案数，可以记作 \(n\brace m\)

递推公式： \(n\brace m\) \(=\) \({n - 1}\brace {m - 1}\) \(+m\times\) \({n - 1}\brace m\)

通项公式：\(n\brace m\) \(=\) \(\frac 1{m!}\sum_{i = 0}^m (-1)^{m - i}\binom mi i^n\)

证明：设 \(G_i\) 表示 \(n\) 个数分成 \(i\) 个集合（可以为空）的方案数， \(F_i\) 表示分成 \(i\) 个非空集合

有 \(G_i = i^n\), \(G_i = \sum_{j = 0}^i \binom ij F_j\)

上一个二项式反演，\(F_i = \sum_{j = 0}^i (-1)^{i - j} \binom ij G_j\)

除掉 \(m!\) 是因为集合没有顺序，\(G_i\) 有顺序

幂多项式转下降幂多项式：\(x^n = \sum_{i = 0}^n S(n, i)x^{\underline i}\)

证明：首先注意到一个组合恒等式： \(k\binom xk = x\binom{x - 1}{k - 1}\)

多来一下 \(k^2\binom xk = kx\binom{x-1}{k-1}=x(x-1)\binom{x-2}{k-2}+x\binom{x-1}{k-1}\)

再来一下 \(k^3\binom xk = x^{\underline 3}\binom{x-3}{k-3} + 3x^{\underline 2}\binom{x-2}{k-2} + x^{\underline 1}\binom{x-1}{k-1}\)

设 \(S(n, m)\) 表示 \(k^n\binom xk\) 中 \(x^{\underline m}\binom{x - m}{k - m}\) 的系数，可以发现 \(S(n,m) = mS(n - 1, m) + S(n - 1, m -1)\) （这种好事

比如 \(k^3\binom xk=kx(x-1)\binom{x-2}{k-2}+kx\binom{x-1}{k-1}\)，这两个式子的原目标都是 \(x(x-1)\dots(k-i)\binom{x - i}{k - i}\)，都会有对应系数的贡献从 \(x^{\underline y} \to x^{\underline {y + 1}}\)。同时，第一个式子会额外加上 \(2x^{\underline 2}\binom{x-2}{k-2}\)，对应 \(\times m\)

现在我们已经证明了 \(k^n\binom nk = \sum_{i = 0}^n S(n,i)n^{\underline i}\binom{n - i}{k - i}\)

要素察觉，注意到另外一个组合恒等式： \(k^{\underline i}\binom nk = n^{\underline i}\binom{n-i}{k-i}\)，直接拆开就可以证

那么结束。

例题：「联合省选 2020 A」组合数问题：注意到组合数 \(\binom nk\)，考虑利用 \(k^{\underline i}\binom nk = n^{\underline i}\binom{n-i}{k-i}\)，所以转下降幂。之后可以利用二项式定理推式子

单位根反演

\(n\) 次单位根 \(w_n = e^{\frac{2\pi i}n}\)

欧拉公式

知道等比数列求和公式

\[\sum_{i = 0} ^ {n - 1} q^{i} = \begin{cases} n&,q = 1\\ \frac{1 - q^n}{1 - q}&,q \neq 1 \end{cases} \]

令 \(q = w_n^k\)

\[\sum_{i = 0} ^ {n - 1} w_n^{ki} = \begin{cases} n &,w_n^k = 1\\ 0 &,w_n^k \neq 1 \end{cases} = n[n | k] \]

单位根反演可以用于化式子 \(n|k\)

[LOJ6247]九个太阳

单位根反演 + 二项式定理

\[\sum_{i = 0}^n \binom ni [k|i] \\ =\sum_{i = 0}^n \binom ni \sum_{j = 0}^{k - 1} w_{k}^{ij} \\ =\sum_{j = 0}^{k - 1} (w_k^j + 1) ^ n \]

取 \(w_k = g^{\frac{mod - 1}k}\) 直接计算即可

[UOJ 450] 复读机

初识生成函数
forever_dreams

没有时间消化了

待办ppt：

后面的 “插值” 的算法、“下降幂多项式“，”第一/二类斯特林数“，”组合数问题，统一省选2020A”，“单位根反演”，“离散傅里叶变换(DFT)”，“离散傅里叶逆变换(IDFT)”，“九个太阳 LOJ6247” 都要么差临门一脚，要么懂了

剩余部分都不大懂，需要花时间

待办网页：

FFT：[教程]快速傅里叶变换 - 博客 - FZUOJ (fzoi.top) FMT/FWT学习笔记 - lcyfrog - 博客园 (cnblogs.com) https://www.cnblogs.com/wyb-sen/p/15779952.html

为什么只给多项式一天时间/fn/fn/fn

7.15-7.15 概率期望组合计数

感觉今天上午整体听起来不错

开头的部分不知道为啥有点蒙，然后中间听到一道题的时候突然惊醒

[AGC028B] Removing Blocks [solved]

naive ：考虑计算区间 \([l,r]\) 的方案数，发现应该是 \(n!*2*inv[r-l+3]inv[r-l+2]\) 但是枚举区间这一步复杂度就 G 了（把 \([l - 1, r + 1]\) 看作一个整体可以更方便地理解）

当然，这里涉及到一个小思想就是说计算方案数可以理解为计算出现的概率再乘上总方案数，也许会更有利于思考

与之相对应的也就是答案 = 答案的期望 * 总方案数

正解：干脆把这个替换枚举顺序搞得更加彻底一点，直接计算每一个点 I 的贡献次数

考虑什么时候 ai 会被算到，假设一个 \(x<i\) 会计算 I ，那么 x 至少是 [x,i] 中第一个被删除的，这样个概率是 \(\frac 1{i-x+1}\)

所以 I 的贡献就是 \(a[i] n! (\sum_{x=1}^{I – 1} \frac 1{i-x + 1} + \sum_{x = i+1}^n \frac 1{x-i+1} + 1)\)

记 \(h_i = \sum_{j = 1}^ i \frac 1j\) ，概率可以简写成 \(h_i+h_{n-i+1} - 1\)

\(O(n)\) 就可以解决啦

当然，这样的思路也可以理解为计算在以键值(I,删除时间)建立的笛卡尔树上深度的期望

笛卡尔树

简单复习一手笛卡尔树

笛卡尔树是满足以下性质的树：树上节点有键值 \(k\) 和权值 \(w\)， \(k\) 满足二叉搜索树性质，\(w\) 满足堆的性质

（小根）构造思路是先保证满足 \(k\) ，所以先按照 \(k\) 排序，考虑依次插入每一个节点，用栈维护

每次新增一个节点，与栈顶比较，若 \(w\) 更大，则弹出栈顶，直到满足

此时，新节点成为栈顶的右儿子，栈顶原来的右子树变成新节点的左子树

其实就是一个不断左旋的过程，可以发现栈中维护的是笛卡尔树最右侧的链

应用：

1. Treap 是树高 \(O(log)\) 的笛卡尔树
2. 以点 \(u\) 为根的子树是保证，\(w_u\) 是区间的最小值的一段连续极长区间区间
3. 区间 \([l,r]\) 的最小值是 \(w_{lca}\)
4. 以及本题中，对于二元组 \((k,w)\)，若 \(k\) 有序而 \(w\) 均匀随机
   \(E(dep_i)=H(i)+H(n-i+1)\)， \(H\) 是调和级数

O(n) 求逆元

\(inv[i]=(P-P/i)*inv[P\%i]\%P\)

例题 [half understanded]

求二元组 \((i,w)\) 的笛卡尔树的所有结点的深度平均值的期望

（当时讲题的时候还在那里复习平衡树/qd 导致根本没有思考）

相当于一个变式，\(E(ave) = E(\frac{\sum h}n) = \frac 1n \sum E(h) = \frac1n \sum (h_i+h_{n-i+1}-1)\)

一路推式子，可以得到 \((2+\frac 2n )h_n -3\)， 所以 \(w\) 根本不重要

由于 \(n\le 10^{15}\) ， cyx 这里为了计算 \(h_n\) 采用了一个数学上的放缩，不了解，略过

[FJWC2018] 残缺的算式[understanded]

为什么没有提交地址/fn/fn/fn

naive1：想到说会构成一个树形结构，以为一个位置的贡献是一路上操作符的合并（忽略了乘法标记）

naive2：考虑 \(E((a_1+a_2) \times (a_3+ a_4))=E(a_1a_3)+E(a_1a_4)+E(a_2a_3)+E(a_2a_4)\)

由于 \(a\) 是均匀随机的，所以随机变量 \(a_1\) 和 \(a_3\) 其实所指的是同一个随机变量 \(x\) （？？？？），所以上述其实等价于 \(4E(x^2)\)

然后发现 \(E(x^k)\) 不会算了，GG

此想法的问题：因为 \(a_1!=a_3\)，所以不能是简单地认为两者等价

正解：同样是考察 \(E((a_1+a_2) \times (a_3+ a_4))\) ，认为其等于 \(4E(a_1a_2)\)

由于 \(a_x\) 在这个乘积中服从同样的分布，所以上述项都是从 \(1\dots n\) 中随机抽两个

（这一步帅炸了 woc ）

设有 \(m\) 项的 \(E(a_1a_2\dots a_m)\) 的系数为 \(f(m)\) ，这个可以通过简单树形背包（只有两个儿子）\(O(|S|^2)\) 得到

考虑计算 \(E(a_1a_2\dots a _m) \times \binom nm\) ，即乘上总方案数

发现这个问题就是说从 \(n\) 个数中选择 \(m\) 个不同数的所有方案的乘积和

设 \(g(n,m)\) ，有 \(g(n,m) = g(n-1,m) + ng(n-1,m-1)\) ，发现就是第一类斯特林数 \(n \brack {n-m}\)

知道答案就是 $ \sum \dfrac{f(m)g(n,m)}{\binom nm}$ ，\(n\) 很大但是 \(m\) 不会太大

暴力计算复杂度 \(O(nm)\) ，瓶颈 \(n\)

构成一多项式需要大胆猜想，看到这种 \(n ≤ 10^9\) 就要往这方面想。

——hhoppitree

观察 \(g(n,m)\) ，如若把 \(m\) 看做是变量 \(x\) ，那么就是这里有 \(n\) 个多项式 \(g_i\)

考虑 \(m \to m+1\) 的转移过程，\(ng(n-1)\) 提高一次，求和最多提高一次

所以 \(g(n)\) 不超过 \(2m\) 次，拉格朗日插值即可 \(O(m^2)\)

更多的解法

[NOI2013]树的计数 [solved]

naive：打摆去了，只简单思考了一下单独根据 dfs/bfs 序可以得到的信息

高度 = BFS 层数 ，问题变成求分层点个数期望

将 bfs 序重排为 1...n ，综合两个序列探究性质：

• \(dfn[i]>dfn[i+1]\) ，则 \(i\) 必然是分段点
• 考虑在 \(dfs\) 序上相邻的两个点 \(dfn[u]=dfn[v]-1\) ，即 \(v\) 要么在 \(u\) 的子树，要么是 \(u\) 的祖先的儿子。此处我们探讨 \(u\) 和 \(v-1\) 的大小关系，因为 \(u<v\) 其实是 \(u \le v\) 的意思，\(u>v\) 当然有 \(u>v-1\)
  • 若 \(u<v-1\) ，此时 \(v\) 只能是 \(u\) 的儿子，所以 \([u,v)\) 必断一层，而这种断层已经处理，所以直接标记 \([u,v)\) 贡献 \(0\)
  • 若 \(u = v-1\) ，此时 \(v\) 是 \(u\) 的儿子或兄弟皆可，无限制
  • 若 \(u > v - 1\) ，此时 \(v\) 是 \(u\) 某个祖先的儿子，无限制

剩下的没有标记的都是无限制，就是不管断不断层，都不会改变 dfs/bfs 序

重排 bfs 序有点实现难度，注意题目输入的是第 i 个 dfn/bfn 是什么

[CF1540B] Tree Array[solved]

这里特别提一嘴为什么在计算两条链第一条先走完的概率的时候直接乘上 \(\frac 12\) 的系数而不用考虑会不会染色到其他点去了

因为考虑染色到其他点，实际上加入了单独只染色这两条链的限制

而这个限制实际上与我们要计算的东西是无关的，是额外的，我们只关注到了染色这两个链之一的时候，染的是哪个

寻求 LCA 次数多，可以考虑 \(O(nlogn)-O(1)\) 的欧拉序+ST表求 LCA

[AGC016F] Games on DAG [solved]

容易把题目转化成 \(SG[1] != SG[2]\) ，此时先手必胜

考虑反向计算 \(SG[1] == SG[2]\) 的方案数

想要使得二者的 SG 值相同，思考 SG 函数的 mex 性质，将原 DAG 按照不同 SG 值染色

问题变成多少种方案使得 \(1,2\) 在同一层

可以想到设 \(f[S,k]\) 表示 \(S\) 集合同色的方案数，怎么转移呢？发现增加一个 SG 值比较小的集合比较方便转移，那转移之后的状态叫什么呢？不能叫 \(f[S\cup T]\) 把，实在是难以转移

所以需要修改一下 \(f[S]\) 的定义，表示 \(S\) 集合中所有 \(sg>k\) 的方案数，同时，如若 \(1,2\in S\) ，保证二者相同

如若对此类 DP 比较熟悉的话，其实可以直接想到从大到小确定各个 SG 值的点集，直接设出状态，相似题目有 [NOIP2018] 宝藏

我们可以每次考虑从未被选择的点新增部分点作为新的一层，然后统计方案。

——Soulist

此时，新增的集合应该比所有的 \(sg\in S\) 要小，不妨直接把原 \(S\) 集合中所有 \(sg+1\) ，视作新枚举的 \(T\) 集合 \(sg\) 全都为 “\(0\)” ，设 \(c[i][S]\) 表示 \(i\) 连边集合 \(S\) 的方案数，那么

• \(S\) 中所有点至少向 \(T\) 连一条边 ，\(\prod (2^{c[i\in S][T]}-1)\)
• \(T\) 中所有点随意向 \(S\) 连边，\(\prod 2^{c[i\in T][S]}\)
• \(S\) 内部连边 ，\(f[S ]\)

特别的是，考虑 \(f[S]\) 的意义，发现如若 \(1\notin S \or 2 \notin S\) ，\(f[S]=0\)

考虑此时若 \(1,2\in T\) ，那么不能直接乘上第三种贡献，此时 \(S\) 内部可以随意连边，所以应该乘上 \(\sum 2^{c[i\in S][S]}\)

从这里我们也可以看出从大往小做的优势，如若从小往大做，便难以计算从大到小连边的方案数

感觉此题的精髓在于状态设计 ，对于 SG 函数性质的观察。

对于题目性质的分析是设计状态的关键

备注：感觉做完之后回头看这道题差点感觉，可能对这道题的本质的理解有缺

[AGC024E] Sequence Growing Hard[solved?]

比较巧妙的一道题，但是 cyx 讲得实在抽象，听不懂，思路来源：tzc_wk

容易发现连续相等段视作在段末增加以去重

那么在 \(i\) 前增加数字 \(x\) 的条件就是 \(x>i\)

发现这个问题实在是有点抽象，感觉不知道应该统计什么，现在唯一需要满足的条件就是每次增加一个点 \(s_i^{\prime} > s_i\)

对关键状态建图可以转化问题

我们现在关注的是加入的新的点和原来的位置的点，二者有新旧关系，有大小关系

我们考虑称在时刻 \(k\) 加入数字 \(w\) 为二元组 \((k,w)\)

如若 \((k,w)\) 在序列上插入到某一状态 \((a<k, b<=w)\) 的前面，我们视作 \((k,w)\) 成为 \((a,b)\) 的儿子

以这样的视角看待这个序列，就成了 \(i\) 位置前面一些是子树，前面不是子树的就是兄弟的子树之类的，大概这个形式

那么，问题就变成了统计有多少颗这样的树，满足儿子的 \(k,w\) 都比父亲大

考虑设 \(f_{i,j}\) 表示大小为 i 的树，使用值域 \([1,j]\) 的方案数

为了不重不漏的考虑，我们可以枚举第一个子树的大小 \(l\) ，那么其的值域必然是 \([1,>j]\) 。

那么现在大致有了 \(f[i][j] = \sum_{l = 1}^{i - 1} f[i-l][j] \sum_{v=j+1}^k f[l][v]\) 之类的，还差不差呢？

考虑到在给这个子树分配具体的儿子的时候，实际上是任意的，因为我们总是可以找到某种方式使得那些被选中的点成为第一个子树的儿子，所以真正的式子是：

\[f[i][j] = \sum_{l =1}^{i-1}f[i-l][j] \binom {i-2}{l-1} \sum_{v = j + 1}^k f[l][v] \]

后面那个 \(\sum\) 可以后缀和，复杂度 \(O(n^2k)\)

[AGC013E] Placing Squares

很容易列出 DP 方程，\(f_i = \sum f(i - k)k^2\) 然后就不会了

观察数据范围，发现 \(n\) 很大，可以猜测是 矩阵快速幂优化/ \(f\) 是多项式

发现都不大行，这个形式显然难以写成矩阵的形式，线性递推做不了。次数太高了，多项式插不动。看题解

考虑 DP 组合意义， \(k ^ 2\) 的意义就是在这段区间中放两个可重叠的黑白球的意思，注意这里球是有颜色的

所以，设 \(g_{i, j}\) 表示当前做到位置 \(i\)，\(i\) 所属的段已经放了 \(j\) 个球。注意每一段放且必放两个不同色

\[g_{i, 0} = g_{i - 1, 0} + [i - 1 \notin X]g_{i - 1, 2} \\ g_{i, 1} = 2g_{i - 1, 0} + g_{i - 1, 1} + [i - 1 \notin X]2g_{i - 1, 2} \\ g_{i, 2} = g_{i - 1, 0} + g_{i - 1, 1} + g_{i - 1, 2} + [i - 1 \notin X] g_{i - 1, 2} \]

\(X\) 表示不能放的位置的集合。

现在就可以暴力矩阵快速幂啦 /hanx

[WF2018] Gem Island

naive：只会暴力。不会计算每一种情况出现的概率，因为当前是那一位增加与手上数量有关

一个很重要的结论就是对于最终每一个人手上拿的 \(a_i\) 的方案出现概率是相同的，在知道这一点之后题目变得好做很多

大概是说考虑 \((a_1, a_2,\dots, a_n)\) 的方案数，首先有一个 \(\binom{d}{a_1 - 1, a_2 -1, \dots, a_n - 1}\) ，然后每一个 \(a_i\) 内部，如果现有 \(x\) 块，那么有 x 中分裂到 x + 1 的方法，内部方案数 \((a_i - 1)!\)

两者相乘就是 \(d!\) ，为定值，所以每一种出现概率相同

整体都砍 \(1\) ，问题转化成了 \(\sum_{\sum a = d}\sum min(b_j, r)\) ,\(b_i = \sum [a_j = i]\)

现在的问题就变成了一类 搭楼梯 的 DP 问题，十分相似的还有 「CH5105」Cookies

需要维护这样的一个东西：

***
******
******
********
********
********
**********
**********

常见的手法是整体砍 \(1\) ，那么所有情况都可以被化归到存在 \(a = 1\)，可以干掉一些枚举量来方便计算答案

对于不同的题目，可以从左往右做，采用上面的手法化归；也可以竖着做，枚举在上面/下面塞一行，计算方案数

常见状态是 \(f_{i,j}\) 表示前 \(j\) 个位置一共填写了 \(i\) 个 \(\star\)

这里，我们记 \(f_{i, j}\) 表示 \(j\) 个数的和为 \(i\) 的方案数, \(g_{i, j}\) 表示在此情况下 \(\sum\min{b_x,r}\) 的和

枚举 $b_1 = k: \(f_{i, j} = \sum_{k = 0}^j\binom jk f_{i - k, k}\)， \(g_{i, j}\) 相应转移

即往下面塞一行

CF605E Intergalaxy Trips

naive：读错题了，以为每次往哪里走是不可以自己选择的，是等概率走向一个方向。勉勉强强列出一个 DP 但是根本找不到优化空间，GG

神仙期望题，一直没看懂，但是 yr 太巨了/bx/bx/bx

设 \(E_i\) 表示从 \(i\) 到 \(n\) 的期望步数，观察这个 DP 转移，发现不算自环是一个 DAG。因为对于 \(E_u\) 而言，我肯定是走到 \(E_v < E_u\)，不然不如走一个自环

既然最后是 DAG，那么我们就可以按照拓扑序转移了。首先 \(E_n = 0\) 肯定是拓扑序第一个点。考虑当前确定了拓扑序前 \(m\) 个点，分别是 \(S = \{a_1, a_2, \dots, a_m\}\)

考虑转移，在不考虑自环的情况下，我们有：

\[E_u = 1 + \sum_{v\in S} E_v p_{u, v} \prod_{w\in S, E_w < E_v} (1 - p_{u, w}) \]

找到 \(v\) 作为下一步，那么此时所有 \(E_w<E_v\) 不能和 \(u\) 联通，不然我直接和 \(w\) 做转移

考虑自环的问题

yr 的理解方式是，现在的 \(E\) 可以理解为不能转移到自环的情况下的期望值
那么实际上的期望值应该是 当前情况的值/当前情况出现的概率，因为 真实值 = 当前的 E \(*\) 不走自环概率 \(+\) 走自环 \(*\) 走自环概率。因为要么走自环要么不走，所以此处的概率可以劣迹为权重

那么我们需要算出不走自环的概率，就是至少有一条边可以走的概率，就是所有边都不能走的反面

所以我们需要给 \(E_v\) “补票”：

\[E_u = 1 + \sum_{v\in S} \frac{E_v}{1 - \prod_{w\in S, E_w<E_v}(1 - p_{v, w})} p_{u, v} \prod_{w\in S, E_w < E_v} (1 - p_{u, w}) \]

更为正统的理解方式是 MoonPie （链接里面的 \(E\) 是补票之后的）

设 \(q = \prod_{w\in S, E_w < E_v}(1 - p_{v, w})\) ，枚举当前停留了 \(d\) 天

\[\sum_{d = 1}^{\infin} q^{d - 1} (E + d(1 - q)) \]

展开可以知道就是 \(\frac E{1 - q}\) ，而 \(\frac 1{1 - q}\) 的实际意义就是走出去的期望天数

唯一的问题是，第 \(m + 1\) 个点是啥。其实就是更新完之后 \(E\) 值最小的点

因为此时所有能更新到它的都已经更新了，类比 dijkstra 的松弛操作，它可以被固定了

\(O(n^2)\)

[ARC016D] 軍艦ゲーム

非常魔法，不知道为什么仅仅是 ARCD

容易列出转移方程

\[E_{i, j} = \min\{E_{1, h} + h - j, 1 + \frac 1{deg_i}\sum E_{v, j - d_v}\} \]

这个式子是有后效性的，但是这个后效性是唯一的，所以可以把 \(E_{1, h}\) 看作主元

由此看来，所有状态都可以表示成 \(kx + b\) 的形式

简单思考之后，发现 \(k\le 1\) ，感性理解是每次取了 \(min\) ，理性一点就是

考虑按拓扑序归纳，考虑 \(x\) 减小了 \(\mathrm{d}x\)，\(f_{n,\star}\) 不会变所以它的导数是 \(0\leq1\)
\(f_{x,j}\) 如果从 \(x+H-j\) 转移来那么 \(\mathrm{d}f_{x,j}=\mathrm{d}x\)
如果从 \(f_{y,\star}\) 转移来，那么 $\mathrm{d}f_{x,j}=\mathrm{d}f_{y,\star}\leq \mathrm{d}x 也是成立的，所以就证明了恒有 \(\mathrm{d}f_{\star,\star}/\mathrm{d}A\leq1\)
—— iMya_nlgau

再感性一下，设 \(g(x)\) 表示把 \(x\) 当作 \(E_{1, h}\) ，计算出来的实际的答案，我们说它是凸的

怎么想呢？考虑 \(x\) 变大，那么取 \(x + h - j\) 的频率增加了，就更加贴近直线 \(y = x\) 了

注意 \(g^{\prime}\) 不一定 \(\le 1\) ，因为这里计算 \(E_{1, h}\) 的时候只采用后面一种转移

既然是凸的，那么就可以二分出 \(g(x) = x\) 的点就是答案

只能说是非常魔法，其中主元法的思想贯穿全文，再希求列出一个方程解出主元的过程中，大胆猜想，仔细观察可以得到这个做法

[USACO18DEC] Balance Beam

为无意义之物赋予意义

神仙题，Mirach 讲得非常到位

没有时间消化了

后面的题好像都听得大差不差？

7.16 ARC144

这把 A 是小学生数学，B 是明显二分答案，被 C 的细节卡了 100min 没做出来

B 第一眼知道要二分答案，但是当时不知道为啥想着“感觉上是二分答案，但是不二分能不能做呢”，浪费了一点时间

C 最开始看成了计算 \(a\) 的方案数，我说那感情好，然后把条件反算，计算满足 \(i-k\le a_i\le i+k\) 的方案数

然后把图画错了，想成了 [AGC036F] Square Constriants /qd

之后突然发现是输出字典序最小的方案/qd

那就只能正向思考了，手模完样例，推出并验证了无解条件

一番推导之后，验证出 \([1,k]\) 取值 $[k + 1，2 k] $ 是可行的，此时 \([1+2k,3k]\) 被限制

一番推导过后，发现 \([1+2k,3k]\) 也有机会取 \(a_i >= i+ k\) 的方案，修改了方案

大致就是根据 \(n\) 和 $2k,3k,4k $ 的大小关系讨论构造方案

然后一直没有过，验证了我构造出来的 \(a\) 确实是排列，剩下时日不多，最后 5min 摆了

yr 过了/bx

结束后看题解，发现最复杂的 \(3k < n \&\& 4k > n\) 的情况推对了，反而是 \(4k<=n\) 推错了，GG

但是实际上 \(4k <= n\) 的时候对于重复状态的观察 是值得借鉴的

此时显然可以先取 \(1+k,2+k,\dots 2k,1,2,\dots k\) ，考虑剩下的位置怎么办，发现这个问题实际上是 \(n-2k\) 规模的子问题，而不能单纯地认为只要有一种合法的方案就可以了，也错得不冤

总体来说，可以接受，C 题的推导过程凝结了思考的精华，是有意义的

DEF 随缘找时间了

7.17 第一场考试

T1T4 原题 /jk ，考场上先把 T1234 都大致思考了一遍

决定先写 T4 正解，然后写 T2 正解，然后写 T3 暴力分，然后写 T1 暴力分，剩下的时间爆肝 T1 正解

但是显然我低估了 T2 的代码细节。。。

吐槽，今天题面锅太多了，还有为什么最后突然说 11:45 结束，T3 暴力没打完

总体来说，考场心态有一点点问题（做 T4 的时候太着急了，因为结论有猜的成分），考试策略还行，最后及时地抛掉了 T2 ，还需要提升代码能力

T1

当场发现 T1 是原题，（靠记忆） 推出了大致思路发现炒鸡细节，说最后再来肝一肝

但是时间分配有点问题，导致最后只剩下 15min 了

写了一个假做法，过了？？？只能说数据太水

Chouti 讲题怎么都在口胡啊，什么叫做“实现一下就好了”

T2

第一步转化比较明了

然后想成了计算 \(\sum max(0,a_p - a_{p - 1} - len)\) ，然后 \(a_p-a_{p-1}\) 大概是固定的这种

觉得这个形式很像 吉司机线段树 干的事情，思考了一个 ST 表维护最大最小值，仿照吉司机线段树的方式，猜测复杂度 $nlog^2n $ 的做法

然后发现假了，因为我可以不动

然后感觉这种形式有点可以建图跑最短路的感觉，但是不会建图

然后从 DP 方向思考，发现难以提取出状态

然后感觉到这种线段比较长，然后就会干掉一些贡献，感觉大致可以考虑整体二分之类的，把一些 \(a_p\) 视作被删掉的

然后想到整体二分是先按照线段长度排序...... 排序？我都排序为啥不直接做，这次被删除的点下次一定被删，做就好了

然后使用了一个 $map<int,set\ > $ ，原因在于错误地以为对于第 \(1/2\) 个点，需要进行奇怪的特殊处理，处理的时候需要根据 \(l,r\) 来找，然后用一个 set ，往里面甩三元组 \((val,l,r)\) 是按 \(val\) 为第一关键字的，不大行

然后就被奇奇怪怪的映射关系卡炸了

待订正，代码实现复杂度rising

T3

没啥思路，暴力 DP 滚粗

正解：知道所有马会在同一个时刻卖出

那么线段树维护即可，当权值因为需要取模而无法比较大小时，可以考虑取 Log 然后比较大小

T4

感到有点熟悉，上了一个分层图最短路，发现过不了样例

手模样例，发现需要正反跑两次，发现需要考虑只经过一条边的特殊情况

1h ？最后有 80 分，发现是 SPFA 被卡了/ll

（SPFA 已经死了！）

7.18 第二场考试

T4 看到那个题面就觉得非常熟悉，赛后一看果然是原题

考场上大致花了 10min 把所有题目大致看了一下，觉得 T124 都比较可做，T3 可能需要观察一下性质之类的

T1 做完之后非常开心， T2 看着简单，但是想歪了，死活整不出来赶紧跳，T3 没敢碰，说先去 T4 拿分

最后 T23 还是不会，T3 简单推了几个小样例不会，按理说输出次大值可以多骗 10 分的样子，但是它绑了 subtask

时间分配（大致）:

10min 纵览 50min AC（对拍后） 1h
30min 想 B 无果 20min 加入 DS 想法 10min 发现DS 想错 20min 放弃 1h20min
10min D BF 1h D AC（对拍后） 1h10min
30min C 乱搞
剩下时间摆烂，存在中间的切换状态时间

今天下午状态不大行，原因是中午没睡好（

今天早饭吃超市，晚饭没吃，打球非常卖力，而且很困，晚上 GG

T1

比预想之中的简单，放在最短路径树上考虑

猜测答案应该是可以三分的，思考具体的判定方法时发现直接枚举 \(x\) 就好了

考虑计算距离超过 \(x\) 的边，可以转化为计算距离不超过的

转化到 SPT 上，就是每一个 \(dis<x\) 的点的返祖边的边权和

考虑到如若两个点 \(dis\) 相同，那么会算两次，干脆把 \(dis\) 相同的提出来单独算就好了

\(O((n+m)logm )\) ，dij，不需要具体把 SPT 建立出来

T2

考场上启发于 \(P\le 16\) 的容斥的部分分，考虑如何快速计算同时覆盖 \(x=1...n\) 个非法点的城墙数量

然后以一个城墙的中心（可能落到线段交点处）作为标识，发现如若不考虑边界，那么一个非法点可以影响到 \(4i -4\) 个长度为 \(i\) 的城墙

发现考虑边界过后贡献成分复杂而且难以通过容斥等手段计算

考虑 DS 暴力维护，一个错误的想法是，根据每一个非法点，暴力使用 DS 标记每一个受影响的中心之后，每一个中心的被覆盖次数是可以 \(\% 2\) 的，那么就可以使用 bitset 了

然后一通乱想，又简单探究了一下 bitset 的使用方法

没办法了，写了个 \(O(h^4)\) 暴力跑了，可恶的 subtask

正解的话，转到以每一个城墙的左上角和右上角为枚举点思考，容易推出成立条件，考虑一条对角线一起处理，可以转化成二维数点问题，离线树状数组/可持久化线段树

（下午订正的时候，甚至把二维数点的形式都推出来了却没有看出来/qd

被一个代码细节卡了：排序不能这样写：

sort(item + 1, item + 1 + cnt, [](Item a, Item b)
 { return a.y == b.y ? a.op == 0 : a.y > b.y; });

考虑如若存在很多 \(y\) 相等， \(op=0\) 的点，那么，在执行一次 \(a,b\) 交换之后，发现 \(a,b\) 仍然可以再次交换，那就 G 了

T3

考场上思考时间较少，大部分时间都在思考骗分/qd

正解：中位数 \(\to\) 二分答案 ，这个 trick 应该以前是见过两遍了的，但是这次还是没有想起来

过程可以转化为一个三叉树的过程，父亲的权值是三个儿子的中位数（类似：神经三叉树，LCT 维护每一次修改的影响范围）

要想使得树根为 \(1\) ，可以设计一个简单的树形 DP，\(f[i]\) 表示使得 $i $ 为 \(1\) ，\(i\) 的子树中最少的值为 \(1\) 的叶子的数量

被代码细节卡了 ：当当前层剩下一个单独的点的时候，这个点应该与下一层的前两个点结合，而不是最后两个

T4

贪心地想到对 \(a\) 排序，那么就是一个区间 DP

区间 DP 猜到决策单调性，打个表观察一下，稍微推一推，结束

7.19 动态规划

虽然昨天晚上睡了 8h ，但是不知道为啥上午还是有点困

感觉 ysy 的 DP 都讲得比较基础，虽然例题不是很基础/qd

感觉 ysy 的讲法就是会了的人听了没用，不会的人听了不懂

——xxx

yysy，讲得不如 pyb，所以他在讲知识点的时候我就去看 pyb 的课件了/hanx

下午接着昨天晚上没咋看懂的 哈密尔顿-凯莱定理 加速齐次线性递推

晚上补了几道今天的 DP ，剩下 30min 左右的时候想着左右做不出题，去看 BM 了

[SRM 563] SpellCards

简单模拟这个过程，发现其实是一个环上问题

naive：把原序列复制一遍之后做区间 DP ，但是发现一个区间被抽掉之后两边回合并，很难做

正解：既然区间会合并，观察选择点需要满足的条件，发现只要 \(\sum l_i \le n\) 就可以了，反正会合并，那我就只关注长度而并不关注到底是在哪个区间发生了这样的贡献

所以就变成了标准的 01 背包

Xorequ

c，我居然没有注意到 \(x+2x=3x\) /qd

条件首先等价于 \(x\oplus (2x) = 3x\) ，然后由于没有注意到上述等式关系，推了半天人傻了

加入条件之后，容易发现等价于二进制位不能有相邻的 \(1\)，简单数位 DP 即可

考虑 \(< 2^n\) 怎么做，发现我最后填写的数可以被划分成 \(0\) 或者 \((10)_2\) 这样的段，所以设 \(f[i]\) 表示长度为 \(i\) 的数的划分方案，那么 \(f[i] = f[i-1] + f[i -2]\)，简单矩快

Ural 1519 Formula 1

插头 DP /tuu

被卡的细节：

• 如若 \((i,j)\) 为下插头，需要保证 \((i+1,j)\) 不为障碍，其他类似
• 对于 唯独没有左插头/上插头 的情况，当前有的插头在括号表示法中可能是 \(2\) ，不能直接认为是 \(1\)
• 由于采用四进制状压，所以数组需要开到 \(1 << (m << 1)\)
• 状态转移搞错了
• Hashsize 过小会 TLE

[JSOI2011] 柠檬

斜率 DP 模板，但是斜率优化的本质实际上是决策单调性，所以我们同样可以在这个问题中套用决策单调性的分析方法

[JSOI2011] 柠檬 题解 - _Famiglistimo - 博客园 (cnblogs.com)

对于 Land Acquisition G 而言，可以视作是本题的弱化版， Flash_Hu 爷爷讲得很好

有几个注意点：

• 计算斜率的时候，使用 double
• 可以以自己作为决策点，这个时候，需要先尝试插入 \(i\) 这个决策，然后清除队首无用决策，再进行转移

小 Y 和恐怖的奴隶主

暴力状态 \(4^8\) 显然不大行，简单观察后发现我们只关注 \(123\) 血的人的数量

所以改设 \(f[i][a][b][c]\) 表示 \(i\) 次攻击之后 \(a\) 个 \(3\) 血， \(b\) 个 \(2\) 血，\(c\) 个 \(1\) 血的概率

依据题意可以得到转移矩阵，注意如若当前有 \(k\) 个，随从被攻击后即使不增加也可以转移

考虑如何计算贡献，想了一阵，不会，在题解的提示下知道要设置一个 \(g_i\) 表示 \(i\) 步的期望，简单推导之后发现应该将 \(g\) 纳入转移矩阵中

多个询问，预处理转移矩阵的 \(2\) 的次幂次，向量乘矩阵处理询问

复杂度 \(O(k^3\log n + Tk^2\log n)\)，卡常，矩阵乘法的中间过程可以使用 int128 而规避取模

被卡的细节：

• 不要以为 \(n\) 开了 ll 就可以了，快读也要开。。。
• \(m =1\) 不能直接输出 \(n/2\)
• \((1 >> 32) \&1 == 1\)

Data Structure You’ve Never Heard Of

你闻所未闻的数据结构！

我的思考：套用树状数组优化 LIS 的方法，预先排序一边求出 rank 之后一样做， \(O(16nlogn)\) ，大概 \(O(n\log ^2 n)\) 的意思

官方：

将一个数理解成为一个二进制集合，那么 \(a\le b\) 等价于 \(a\) 是 \(b\) 的子集

有两种暴力思路：

• \(f[i]\) 表示以 \(i\) 结尾的 LIS 数量，修改 $O(1) $ ，询问 \(O(2^d)\)
• \(g[i] = \sum _{j\le i} f[j]\) ，直接求解 \(g\) ，修改 \(O(2^d)\) ，询问 \(O(1)\)

考虑 平衡修改查询复杂度

$f(i,j) $ 表示前八位为 \(i\)，后八位是 \(j\) 的子集的方案数。

转移的时候枚举 \(i?\) 的子集，取出 \(f[i][j]?\) ，然后贡献 \(f[i][j\le k]?\)

复杂度 \(O(n 2^{\frac d2})\)

没有时间消化了

剩下的题都挺有意思的，最后一道题当时摆了

7.20 自主消化

好！没有考试，没有讲课

上午都在学 BM ，练习了一道 BM 的题，在下午 15:00 回到昨天的 DP

一直做一直做，晚上做烦了，有点颓

7.21 图论

今天的题都挺有意思的，fsy 每道题之间都留了很多的思考时间，但是我想一会就没思路了/kk

SCU 4444 Travel

考察对 BFS 的理解

分类讨论之后容易发现我们需要在补图中执行边权都是 \(b\) 的 BFS（然后就不会了/qd

考虑 BFS 执行过程中需要的到底是什么，BFS 大致思想是从已确定点中向外扩展，松弛可扩展点并入队。保证每一个点第一次松弛的时候就是最短路（边权相同/只有 01）

设队首 \(u\) ，连出的点集 \(S\) ，设实际上可以扩展的点集 \(V\)

\(V\) 中显然需要去除以前就松弛过的点，\(V\) 中显然需要去除 \(S\)

所以我们只需要用一个可删除（双向）链表维护没有更新过的点的集合 \(V\) ，每次遍历 \(V\)，若当前点 \(\in S\) ，那么跳过；否则更新并从 \(V\) 中删除。

\(\in S\) 的情况最多 \(O(m)\) 种， 一共删除 \(O(n)\) 次

复杂度 \(O(n + m)\)

WOJ 4701 Walk

讲题的时候怎么不给数据范围啊，搞得我以为我的想法不够快

容易想到可以仿照 FWT 的方式优化建图

具体的， \((i,val_i, 1)\) ，\((val_i, i, 0)\) , \((val_i, val_i-(1 << x),0)\) 其中 \((val_i >> x)\&1\)

然后可以跑个 \(01-bfs\)

BZOJ 2259

第一眼 P3203 [HNOI2010]弹飞绵羊，但是 LCT

第二眼 ARC122F Domination ，发现本题就是这道题的超级弱化版，结束

复习了一下 ARC122F ，想出了大体思路，AT \qiang

墨墨的等式

同余最短路 模板，非常巧妙

同余最短路是一种优化最短路建图的方法

通常是解决给定 mm 个整数，求这 mm 个整数能拼凑出多少的其他整数(这 mm 个整数可以重复取)或给定 mm 个整数，求这 mm 个整数不能拼凑出的最小（最大）的整数。

——Ariel_

思想：将问题分成两部分，求出一个部分的最优解然后和另一个合并

这个思想很像 meet in the middle ，在此处的题目条件下，就变成了同余的关系

弱化版：P3403 跳楼机

「HNOI2019」校园旅行

很妙的题，但是因为并查集写错了，被卡了 1h /fn/fn/fn

void find(int x) { return f[x] = x ? x : ..... }

还有：

f[i][1] = f[i][2] = 0;
...
f[u][0] = v;

/fn/fn/fn，但是调题技艺有所长进（？

——

第一眼：P7323 [WC2021] 括号路径 ，然而并不是。然后就只会暴力了

正解：暴力复杂度 \(O(m^2)\) ，考虑把这个 \(m\) 搞得小一点，不同于括号路径，此处权值只有 01 两种，所以应该是有比较大的优化空间的

考虑一个联通块中的颜色相同的边组成的图，可以发现，如果这张图是二分图，那么只保留一颗生成树答案不会变，因为可以在一条边上反复横跳，这样反复横跳不会改变奇偶性，但是因为没有奇环，所以无所谓。如若有奇环，那么就随便补上一个自环即可

对于联通不同颜色的边，此时肯定是黑白黑白交错的二分图，同样可以只保留一棵树

这样边数就是 \(O(n)\) 级别了

TopCoder 12330 Coins Game

考察两个点之间的关系，发现如若 \(a,b\) 无法满足要求， \(b,c\) 无法满足要求，那么 \(a,c\) 也不可以

所以解法就是考虑求出这样的最大的团，用总方案数减去就好

可以使用 bfs 处理满足条件的点对。扩展状态的时候注意分析如果前一步被挡住了，那么实际上应该判断背后有没有石头

CF843D Dynamic Shortest Path

数据范围支持 \(nq\)，所以大概的构思就是先跑一遍最短路，然后再希求一个 \(O(n)\) 每次的更新方法

\(O(n)\) 最短路可以想到 BFS，它与 dijkstra 没有本质不同，都是在第一次访问的时候就确立最小值，只不过由于值域原因，dij 上了一个小根堆，多了一个 log 的复杂度

关注到这里每次增加的边权都是 \(1\)，所以 BFS 觉得它很行

考虑设 \(ad[u]\) 表示 \(u\) 增加的距离，\(dis[u] + ad[u] + edge[e].dis - dis[v] \to ad[v]\)

只用管 \(ad < min(c, n - 1)\) 的部分

bugs：

• 开 long long！不然会导致 \(ad\) 算出负数导致 RE
• 对于 \(ad == inf\) 的点，不一定是不可达，所以 \(dis += ad == inf ? 0 : ad\)

CF1305G Kuroni and Antihype

c，这道题思考太少了直接看题解，看了题解代码写得和题解一模一样，mmp，多少有点问题

感觉这个贡献方式很烦，因为对于一个生成树，树根是没有贡献的

方便的贡献方式是每一条边贡献 \(a_i + a_j\)，可以想到先把 \(ans -= \sum a\)， 然后就可以了

为了使得最后形成的是一个树而不是森林，可以手动增加一个 \(a_{n + 1} = 0\) 的点

（懂不懂什么叫做 For convenience 啊

暴力做可以从大到小枚举边权，然后枚举子集，并查集合并 \((3^18\alpha(n))\), \(18\) 是 \(\log V\)

考虑优化这个过程，使用某 B 姓算法，现在需要快速找到一个集合向外最大边，也就是计算集合中每一个点向外的最大边

可以设 \(mx[S]\) 表示 \(\max_{T\subset S} a_T\)，那么对于一个 \(a_i\) 而言，最大边就是 \(mx[ALL ^ a[i]]\)

问题在于可能出现连向同一个连通块的边，解决方法是维护一个和 \(mx\) 在不同连通块的次大值，具体实现的时候可以用一个 \(pair\) 记录值的大小和所属连通块编号

\(mx[S]\) 可以通过 FWT 的方式转移，或者保证只从 \(mx[S^(1 << highbit)]\)

对比之前的暴力为啥需要枚举子集，可以从一个角度感性为什么 FWT 可以优化复杂度。可以把 \(f(S) = \sum f(T)f(S\backslash T)\) 看作是一种卷积，而我们这里变成了 \(F(S)=\sum F(T)\)

复杂度 \(O(18 2^18\log n)\)

没有时间消化了

剩下的很多题都是懂了的，都可以写

除去：King's Road Reachability CityRebuild(差点) Determinant of a Graph

7.22 最大流

事实说明，可能 fsy 讲得是没有问题的，如若经过了充分思考，听懂他的讲解应该是轻松的

最大流/se/se/se，感觉今天的题都很有意思啊

最后看着写不了几道题了，就决定干脆把今天对题目的思考记录一下，不然忘了

晚上状态不大好，调完 T2 之后把剩下的题大致浏览复盘了一下，然后帮 wyx 调了一下 T2

简单学了一下最小割树，剩下的时间在看gym102220 A

要放假了，感觉心神松懈下来之后非常困，趴了 5min

小注：understanded 表示还没有写代码

CF884F Anti-Palindromize

naive:

首先可以贪心地想尽量保留更多的位置，那么对于当前满足回文限制的位置，我们考虑如何交换，然后不会做了（但这个其实就是 官方题解 的做法）

没有事干，因为要求反回文串，所以考虑把这个 \(s\) 拆成 \(\frac n2\) 的两部分，然后写成两行的样子，这样好看一点

由于标题是网络流，所以我们考虑网络流

由于每一个字符只能使用一次，那么可以想到建立 \(26\) 个节点，源点向每一个节点连流量为字符出现次数的边

然后感觉就把那两行摆出来，然后乱 gb 连一连，处理一下限制就可以了？当时想到这里，没有更多时间来具体思考到底应该怎么连边了。因为最开始的时候在划水没有思考

正解：

具体连边方式如下：

考虑 $\frac n2 $ 个点在 \(26\) 个点的右边一字排开，左边每一个点都要向右边的点连边，流量均为 1，考虑费用

• 原串中这个位置字符都是当前字符，那么连边 \(\max\{b_1,b_2\}\) ，分别指原串中对应位置的 \(b\)
• 原串中这个位置字符存在当前字符，连边 \(b_i\)
• 连边 \(0\)

然后 \(\frac n2\) 向汇点连 \((2,0)\) 即可

理解：

需要满足 4 个条件：

1. 放回去之后，每个字符的出现次数必须跟 \(s\) 中的一样
2. 放回去之后 \(t_i \neq t_{x-i+1}\)
3. 每个位置能且仅能放一个字符
4. 价值最大

为了满足第一个，我们借助了分配流量的手段

为了满足第二个，我们控制了字符向 \(\frac n2\) 点连边的初度

为了满足第三个，我们控制了 \(\frac n2\) 的出度

综上，这道题其实考察的是对于网络流限制和流量的关系的理解

[BZOJ4205] 卡牌配对

naive ：读错题了。。。。以为需要自己划分 \(X,Y\) 两类

所以思考的是假装我把可以配对的都用某种方式连起来之后，我应该怎么做才能在保证恰好分割成 \(n1,n2\) 个点的前提下求“最大割” /qd

然后不会

正解：

题目是 最多一个不行 ，也就是至少两个可以

一般我们看到 xx 不行的时候，想的都是计算出这样情况下的贡献然后用总方案减去，即容斥的思路

但是这里想要的是优化建图，所以就换一个表述方法以正向求解

枚举哪两维满足条件，建立虚点 \((2,3),(3,5),(2,5)\) 之类，如果 \(p|a,q|b\) ，那么让 \((a,b,c)\) 和 \((p,q)\) 连接

注意三种方式不能边不能混在一起跑，要简单分层

被卡：

• 虚点和 \(S,T\) 存到同一个位置了/qd （下标分配错了
• 数 组 大 小 算 错 了，以 为 写 挂

卡了亿么久

UOJ 77 A+B Problem

讲课的时候独立想出来了/hanx

第一眼：高配版 P1361 小M的作物 ，然后凭着记忆大致复原了一下弱化版的建图方法，想清楚了割边的意义代表选择另外一个，对于组合起来的附加贡献，只需要构造边使得选择了对应组合之后图仍然联通即可。

（其实好像本来对 小M的作物 的具体构造思路就有点忘，当时好像也不大懂，这把属实是整体实力带动起来了）

然后考虑这个附加贡献是什么意思，当然可以暴力连边，但是需要优化建图

那就可持久化线段树即可

另外一种建边方式是，发现这个其实是一个二位偏序问题，那就套用 CDQ 分治的做法

最小割解决的就是分成两个集合，求最优解，带限制的题

——fsy

bugs ：

• 想清楚跑的最大流的意义
• 注意到 \(p_i\) 只能被计算一次，所以需要对 \(1\sim n\) 向 \(n + 1 \sim 2n\) 连权值为 \(p[i]\) 的边，然后交给 \(i + n\)
• 最大流写错了

BZOJ 2400 Optimal Marks

我的想法：经典二进制位互不影响， 然后就可以借用上道题的思路了

唯一的问题是如何选尽量少的 \(1\) ，当时的思考是看作一个二维的问题，那么可以用最小费用最大流，直觉上是可行的，但是网上似乎没有这个做法，有时间可以尝试一下

fsy 的想法：如果不管最大流的限制，考虑对选取最少的 \(1\) 建立一个网络流图

一个简单直接的想法就是把这两个最大流图对应边相加起来就可以了

但是这样会有影响，那么为了表达一种主次关系，我给最初始的网络流图的边权乘上 \(10^6\)

这样，最后的割值被表达为 \(a\times 10^6 + b\) ，\(a\) 是最小边权，\(b\) 是最少 \(1\)

AGC038F Two Permutations[understanded]

naive：（有点忘记当初的想法了）把每一个 \(a_i,b_i\) 搞成出度为 \(2\) 的样子，然后把两者相等的贡献视作之前提到的 小M的作物 中的组合贡献，可以表达在费用上

但是 \(n\) 太大了，又不是二分图，直接 T 飞

正解：

观察性质，发现实际上存在一种联动机制，就是说对于一个环而言，其中任意一个点选择变成 \(i\) ，那么整个环都要变，所以现在就可以把一个环当成一个整体进行考虑

All Pair Maximum Flow

震惊我一百年的题

naive：P4897 【模板】最小割树 但是暴力最小割树的复杂度是 \(O(n^3m)\) ，即使跑不满也不大行

sol：

发现题目中所给的图是一张平面图，不妨转成对偶图来考虑。
考虑外侧权值最小的边 e，边权为 w，它对应里面的平面区域为 u。如
果最短路经过点 u，易证边 e 一定被跨过。所以可以将边 e 删去，u 的
其他边的边权加上 w。
删完之后就得到了最小割树，用一个 Kruskal 重构树统计答案即可。

注意这里只是”转成对偶图考虑“，实际上并不需要转成对偶图

Gym102220A Apple Business

官方题解：The 13th Chinese Northeast Collegiate Programming Contest - Claris

naive：只会暴力费用流/qd

具体的，\(S\) 向每一个询问链接流量 \(c\), 费用 \(w\) 的边，询问向对应点链接 \((inf, 0)\)， 每一个点向 \(T\) 链接 \((a, 0)\)

sol：

非常玄妙的好题，树形 DP 闪瞎狗眼

模拟费用流，发现显然会先跑 \(w\) 最大的，而且 \(w\) 小的不会替代更大的，也就是说从大到小处理每一个询问，每一个询问都是在不改变前一个询问的前提下尽量拿。

难点在于要合理地为后面的 \(w\) 留下一些点的意思。

假装现在求出了一个具体的销售方案 \(d_i\)，考虑暴力判断这个方案是否合法。直接把 \(S\) 到每一个询问的流量改成 \(d\)，此方案合法当且仅当每一条 \(d\) 边都满流。

图是二分图，满流就是完美匹配的意思，借助霍尔定理，完美匹配等价于任意一个左部子集对应的右部点点数 \(\ge\) 左部入容量总和

放到题目给的二叉树上，就是二叉树上每一个连通块中 苹果数量 \(\ge\) 路径两端都在联通块中的路径的销量和

实际上这里可能出现多个连通块的情况，但是保证了每一个都满足，多个连通块自然也是没有问题的

注意到这里 \(u, v\) 的路径都是直上直下的，为了计算当前路径最大 \(d\)，很自然想到枚举 \(u\) 的父亲 \(x\)，计算在 \(x\) 的子树中，包含 \(x,v\) 的联通块的，最小的 苹果数量-路径两端都在联通块中的路径的销量和 的值

设 \(g_{x,y}\) 表示在 \(x\) 的子树中，同时包含 \(x,y\) 的联通块的 xxx 的最小值。计算的是起点在 \(x\) 到 \(v\) 的路径上，终点在 \(y\) 子树内的路径。

单个点也可以看作是一个连通块，设 \(b_{x,y}\) 表示 \(y\) 在 \(x\) 的子树中的贡献，初始值为 \(a_i\)

每次确定 \((u,v)\) 销量 \(d\) 之后就枚举 \(u\) 的父亲 \(x\)，让 \(b_{x,v} -= d\)。可以理解为把一条路径浓缩成一个点，一方面是单点也是连通块，另一方面是保证了 \(b_{x,v}\) 计算的是 \(x\) 子树内的路径

有 \(g_{x,y} = b_{x,y} + \min(0,g_{x,y*2}) + \min(0,g_{x,y * 2 + 1})\) 。取 min 是可以不选，最后选出来反正是一个连通块

考虑计算 \(u,v\) 的最大销量。枚举 \(x\)，想清楚 \(g\) 的定义，合并上起点在 \(x\) 到 \(v\) 的路径上，终点不在 \(v\) 的子树的 \(g\) 值。

由于树高 \(log\)，所以上述操作都是 \(\mathcal{O}(log^2)\)

没有时间消化了

剩下的都不大会

7.23 ABC261

ABCD 语法题，但是被 C 题奇怪的 cin 卡到了

E 第一眼二进制位互不影响，第二眼是矩阵优化，观察到每次操作都差不多

然后发现矩阵做不了，然后发现没有必要上矩阵，随便预处理一下就可以了

数组开小了/kk

F 最开始在考虑建模转化，发现不大行

然后考虑到对于每一个颜色单独来看的话，可以视作每种颜色内部是有序的

即可以假装一些东西已经排好序了，不需要再操作了

思考一下这部分“排好序”的东西的影响，发现就是内部的逆序对数量

所以答案就是 总逆序对数 - \sum 单个颜色逆序对

G 最开始以为是加强版 P1032[NOIP2002 提高组] 字串变换 ，准备给他上个双向搜索+最优化剪枝+随机化搜索（到时间就不搜了，多交几次）

写了写发现随便卡，/qd，抛掉了

Ex 感觉这个模型很熟悉，但是不大会，GG

GEx 随缘补了

7.24 第三场考试

去经历风浪

这把打的时候信心满满，自以为口胡出了 T1234，考完发现都是错的

7:40 Start
7:55 T1：想到主席树优化建图 + 不删除莫队询问 + 网络流 = 信仰过题
8:10 T2：想到暴力最小割（平面图转对偶图） (联想 [当年CSP] 交通规划)
8:19 T2：想到二维数点 + 线段树 (联想 gls 讲的某一道题，动态(?)维护凸壳)
8:36 T3：简单树形 DP
8:45 T4：整体二分即可
8:50 开写 T3
9:10 洗完脸反而神志不清。。。
10:30 放弃 T3
10:55 写完 T1 暴力
11:20 放弃 T2 暴力
11:45 T4 正解乱刚无果

昨天晚上包括今天中午都睡得不大好，睡觉的伤害 bhr 开着灯，等到 bhr 关灯了，czl 的呼噜声着实有点大声（

一想到这个成绩将和之后的 NOIP 有联系，就觉得很自闭，中午睡觉的时候在哪里胡思乱想，mmp

下午来的时候有点颓废，本来还说至少思路没啥问题，呵呵

听完讲解，T123 可能就剩下代码实现问题了，T4 讲得太烂，感觉 ysy 好像也不大会

振奋起来！振奋起来！振奋起来！

打球发泄了一下，好多了

今天晚上有点不集中，原因是 QQ 音乐把一首很好听的歌给我搞丢了

只订正了 T1，T2 放弃了， T3 没写出来， T4 正在写

T1 「JOISC 2016 Day 1」俄罗斯套娃

naive：

考虑 \(q=1\) 的情况，发现套娃不能一个套多个，满足了一种匹配的关系，考虑二分图匹配

发现这个边的数量有点多，可以考虑上一个主席树优化建图之类，然后这个是二分图匹配，可以信仰 Dinic 的复杂度（当前弧优化！vis！ISAP！）

然后发现如果增加了点的话，那么就会增加一些流量为 \(1\) 的边，可以使用 FF 在跑一跑，复杂度可以接受

不会处理删除点的情况，考虑模仿不删除莫队的方法移动我们的指针，反正 FF 复杂度 \(O(mf)\) ，\(f = 1\) ，然后残量网络上 \(m\) 的大小大概也是可以信仰的。这个思路来自 CF1383F Special Edges 题解

想得很快，但是一点都不敢写/qd

正解：

仔细考虑第一句提到的匹配关系，发现实际上是有贪心的内核在的，也就是说如果二分图匹配过程中左边有 \(n\) 个点，直接贪心地把左边依次分配就可以了，因为左边第一个的取值范围始终是包括下一个的

然后如若把具体的套娃关系在二维平面上表示出来，或者说观察一下上述的二分图匹配的结果，发现实际上就是一个最小不交链覆盖的问题。

也就是说，在二维平面上，我们可以把点划分成很多条不上升子序列，可以把点分层，对应上面所述的贪心的最大匹配的过程。其实也就是 节点数-最大匹配 = 最小不相交链覆盖 （证明)

这个定理叫做 Dilworth定理 ，更一般的模型是 导弹拦截

又是一个常见转化 最小链覆盖 = 最长不上升子序列

也就是说，我们定义 $a_x < a_y,b_x < b_y $ 表示两个点可达，那么最小链覆盖 = 最大的不可达的团 = 最长不上升子序列

更严谨的表述可以看 Shiina_Mashiro

为了辅助理解，可以看 Hëinz 中的图片

所以现在的问题变成了动态处理这样一个最长不上升子序列的问题

由于保留的是 \(a\ge A, b \le B\) 的点，所以我们考虑对于 \((a,b)\) 按 \(a\) 降序，\(b\) 升序排序，询问同样

上个树状数组即可，大概是一个前缀 max 的样子

T2 [NOI2016] 网格]

naive：

把题目意思转化成了割成两个点集，联想到 [CSP-S 2021] 交通规划 题解 ，然后说枚举一下 \(S,T\) 所在角落就有 \(nmlog(nm)\) 的算法了

然后考虑这个拼路径的过程，延续 Y - Grid 2 (atcoder.jp) 的思想，想到在要利用已有障碍的情况下，我想要知道的是一个障碍到 左下、右下、左上、右上 某一个边界所需要增加的最少障碍。这显然是一个二维偏序的问题，上个线段树之类就可以处理左下，然后转一转坐标轴就好

这个做法假的很离谱，原因在于没有必要是划分开整个块，可以采用包围一个的方式

正解：发现答案只有 \(-1, 0,1,2\) 四种，但是 \(2\) 很难判

判断前三种，那么都不行的话直接输出第四种

特判只有一行/一列的情况

T3 P3647 [APIO2014] 连珠线

naive:

显然是树形 DP ，但是当时想得太快了，把题目极快得转化成既可以选儿子和孙子，又可以选两个儿子，但是选两个儿子只能选择一次

然后设 \(f[i][0/1]\) 表示当前点 没有/有 留下儿子的最大价值，然后 @#$%^&* 就好了

还是比较细节的，调了一段时间，实现思路是先不管两种儿子合并的情况，然后计算一下 \(\max{dlt}\) 之类。注意可能儿子只有 1 个。

然后发现大样例搞出来比答案大得多，GG，以为是自己算重了之类，反复造小数据手膜，发现按照这个想法，这个实现是没有问题的

（你一开始就搞错了啊喂）

搞了 1h30min 骗了 10pts /hanx

正解：

发现两个儿子合并的情况只能出现在根，剩余贡献方式唯一

所以设 \(f[i][0/1]\) 表示 \(i\) 作为蓝线的端点/中点的最大值，考虑到换根的问题，在设 \(g[i][0/1]\) 表示往上走的贡献

然后枚举每一个点，把 \(g\) 当做子树重算一下即可。

T4 技能树

给定一棵树，每次操作可以删除不超过 \(k\) 个点，要求这次删除的点的父亲在之前某次操作中已经被删除了，问删完整棵树的最小操作次数，多组询问

naive：

一来就想，那我肯定是贪心地能删则删啊——那么如若多个子树可以选择，你选哪个啊

然后再一想，说我现在可以 \(O(n)\) 求出一个 \(k\) 的操作次数了（？），我多个 \(k\) 咋做

然后口胡了一个“整体二分”，每次二分出如果想要 \(\le d\) 天完成，\(k_{min}\)

但是复杂度都是错的，阿姨，整体二分之所以是 \(log\) ，在于每层只操作 \(r- l +1\) 次，然后有 \(log\) 层，那么总共操作 $ nlog n$ 次。GG

正解：

只能说是性质观察比较 nb，在观察性质的时候，可以从弱化版起手

比如 ysy 就是先转化为序列上每次选 \(k\) 个数 \(-1\) 进行观察

结论：固定 \(k\) ，\(ans = \max\{i + \lceil \dfrac {s_i}k\rceil\}\)， \(s_i\) 表示 \(i + 1, \dots n\) 层的总点数

简单证明：意思就是说，前 \(i\) 步干掉了前 \(i\) 层，后面所有操作每一下都能删 \(k\) 个

主要是证明可以取等，如若下一层取不到 \(k\) 个，那我这一层少取一点就好了。

（这里其实不是很懂，广附老哥的证明总感觉有点奇奇怪怪，感觉逻辑不是很清晰，奇奇怪怪的）

或者说容易发现合法的 \(j\) 只会有一个，其它状态都会偏小，所以取 \(\max\) 可以保证转移的是这个

发现这个式子可以斜率优化

7.25 第四场考试

时间轴：

7：35 STATR
7：40 发现 T34 题目很长，这把可以多给 T1
8：10 T1 大致想法
8：38 发现 T1 复杂度算错了/ll
9：00 T1 BBBBBBBBBBBBF 打完
9：05 发现 T1 不用离线。。。（BIT -> 离线 -> 预处理 pre suf 即可/qd）
9：20 开始加随机化骗分
9：30 走出 T1
9：40 写完 T2
10:00 发现 T1 有大样例然后修锅/qd
发现是变量名写错了/qd
10：15 来到 T3 第一眼期望概率乘上总方案数..... 显然不大行
考虑斜率在区间内，斜率截距均可以三分，暴力做法有了，但是好像精度不大行
考虑树上莫队，即考虑拟合使用增量的思想（莫队二次离线/jk）
11：25 考虑到 T4 2-sat 优化建图的方法，但是只能过前 30
发现 2-sat 忘记了，没敢写，补充 T3 暴力（最后 5min 狂敲 1k+）

T1 废了， T2 假了，T3 挂精度了 /wx

中午简单交流之后大致就知道结果了，心累，有点撑不住

知道其实是提升的好机会，但是即使知道怎么做，也不是很想写代码

不要为了打暴力而打暴力，一定要先总览全局评估难度分部

每一道题思考时间加足，想清楚再写

T1 「SHOI2017」期末考试

最开始感觉很像接水问题之类的，发现不是

又感觉有点像 ARC122F Domination ，发现不是

然后秉承着打暴力的思想，先把这个问题形式化了一下：

最小化：

\[C\sum [ori-x-y>t_i](ori-x-y-t_i) + Ax+By +Others \]

\(ori = \max\{b\}\) ，即对原最大值做 \(Ax\) 和 \(By\) 并保持它是最大值，\(Others\) 是为了保持最大值的代价

想到枚举 \(x,y\) ，想到 \(x,y\) 肯定有范围吧，为了保持最大值， \(\lceil \dfrac{sum - ori + x}{m -1}\rceil \le ori - x -y\)

可以推出 \(x\le \dfrac{(1-m)y-sum + orim}{m}, y\le \dfrac {xm + sum - orim}{1-m}\)

大致是这个意思，然后发现值域有 \(1e5\)，但是部分分值域\(2000\) 的话枚举量 \(2e6\) 左右，是可以做的

对于 \(Others\) 和前面那个 \(\sum\) ，可以随便用 离线/排序后处理前缀和 轻松处理

然后就这个算法调了半天，把特殊情况也打了，最后想着剩下一档分不能啥都不做，写了一个随机化骗分上去。

4.7 kb

正解：

枚举最大值，对于 \(Others\) 和前面那个 \(\sum\) ，可以随便用 离线/排序后处理前缀和 轻松处理

/wx/wx/wx

（本来说写总结排解心情，调整状态，怎么越写心态越炸呢

upd 16：26 pyb 的化疗/bx，确实有动键盘太快导致正解被蒙蔽的因素，当时想着赶紧把暴力打完

T2 「ZJOI2007」报表统计

思考没有加足

简单 STL 运用，考场上太慌张了，因为被 T1 心态卡炸了，读完题，简单手模之后就开始乱写

然后忽略了可能插入一个数会使得原来相邻的不相邻，即无法贡献

当时觉得有点奇怪，感觉不大对，但是想着只剩下 1h30min 不到，后面还有两道题的暴力没打。后面也有回头看，但是思维被蒙蔽了，不仔细，满脑子都是 T4 如何建图

（咬牙切齿

小剧场：

T1：你忘记以前模拟赛的时候对我的一心一意了，呜呜呜，居然还想打 T34 的暴力

T2：呜呜呜，我没有大样例不知道手造吗。直接写正解不写部分分是伞兵麻。100 分不要了去打暴力干啥

只能说不够沉稳，该做的程序还是要做的

感觉以前打模拟赛爆肝也是有一定问题的，但是当时只会打低档暴力，意义确实不大，不如努力挖掘思维深度

尽人事，听天命

T3 [ZJOI2014]星系调查

naive：发现好像暴力分很足？每次询问直接把对应的点提出来然后直接上三分套三分求解直线即可，暴算点到直线距离和。期望 50。发现精度有点着不住（乘除运算太多了），但是开了个 long double 就没管了（没有进一步推式子的意识）

然后疯狂分段暴力处理 5.1 kb /qd

教训：有精度要求，肯定是要进一步推式子的。

联想：NOIP 2021 方差，暴力推式子啥用没有

正解：数学推导成可以树上差分维护的形式

T4 「JSOI2019」精准预测]

第一眼 2-sat ，想到了可以缩点，想出了 40？ 的暴力。但是感觉细节太多，不敢打。

正解：根据 2-sat 性质建图，缩点之后跑传递闭包，bitset 优化。卡空间，分块跑传递闭包。

7.26 讲题选杂

/qd，今天上午这位讲课速度超过常人而且稍微走神一道题全掉，根本连不回来。

yjz：有没有问题？
wyb：（内心独白）您重来一遍？

这把上午听课的时候越听越困，感觉脑细胞死得格外快，不知道是什么原因

另一个方面来说，幸好这位讲的不是很细，不会太亏。

今天的题都很有意思。

下午努力消化了一下上午的部分题目，把一些半懂不懂的搞得差不多了

晚上努力写题，中途发现我的博客居然有人看，连忙回头复习了一下子树信息的统计方法：DSU on Tree/线段树合并/ 分治 dfn 序 （CF600E）

CF1286E Fedya the Potter Strikes Back [solved]

naive：Z 函数，发现对于一个 \(L\) 而言可以计算到多个 \(R\) ，大概是会算重的，思考了一下，不大好算。考虑交换枚举顺序，以 R 为基准，考虑现在怎么计算......（没有时间想了

正解：讲课的时候听不懂，原因是换成考虑 \(R\) 之后，题意被理解错了，脑海中的字符串关系发生了错位，直接 G 麻了

先想暴力，增量法， 动态求 KMP， 发现所有以 \(r\) 为区间右端点的区间可以通过不停跳 fail 得到。那么 \(O(n^2\log n)\) , \(\log\) 是因为区间最小值

对于跳 FAIL 操作的理解：可以贡献的区间 = Border， 跳一次 fail 是最大 border，所以一直跳到 \(\rm 0\)

容易发现复杂度瓶颈在于寻找 border（跳 fail）的过程，考虑动态维护 border 集合

暴力维护的方法是：考虑每次末尾新加入一个字符，如若 \(s[1] == newchar\) ， 那么 border 集合增加；对于原 border 集合，如若这个 border 续不上，需要把这个 Border 删除

注意到 border 最多 \(n\) 个，所以插入/删除是 \(O(n)\) 次，均摊 O(1)，先不考虑随着 border 删除带来的答案变化，时间瓶颈在于寻找到需要删除的 border

一个处理方法是记录 \(anc[i][26]\) 表示 border [1,i]， 前一个（fail 树上）后继字符为 \(j\) 的 border 的位置。

考虑贡献计算的问题。在删除一个 border 时，需要询问它的权值，可以通过单调栈 + 二分解决，另外一个比较粗糙的方式就是干脆再来一个线段树。需要用 \(w_i\) 去更新（推平）单调栈的一段后缀，用 map 维护每个权值以及出现次数，找到 >w 的直接暴力推平。

暴力推均摊 \(O(\log)\) ，因为被推平之后就被合并成一个新的了。

回头来看，这道题整体思路还是很顺畅的，见多识广一点，需要什么就维护什么，什么复杂度高了就干它 如果你真的干得动

CF1464F My Beautiful Madness [solved]

非常有意思的题

naive：暴 力 判 断

正解：难以判断路径关系，欲求一种简单的等价的容易判断的表示法

可以想到抓出树上某一个关键点，这个点需要满足的性质是如果有解，那么它必然处于所有路径的交集

经过脑洞画图分析思考，这个点它的限制必然是最大的，也就是最影响是否成立的，那么它要比较偏远。但是又不能太偏，不然盲目增加额外限制。

我们说它就是 最深的 lca 的 \(d\) 级祖先，感性理解，因为是最深所以限制最大，因为是 lca 代表一条路径的最高点所以不至于太偏。发现这个 \(lca\) 子树中肯定是没有路径了，这个限制感觉还是有点紧，所以可以往上面尽力白嫖 \(d\) 步。（强行解释.jpg）

当然也可以理性证明一下，设这个点(最深的 lca 的 \(d\) 级祖先)叫做 \(u\)，即证明 \(u\) 是所有路径的 \(d\) 邻居 \(\Leftrightarrow\) 所有路径有交

子树内外分别考虑，对于子树内的路径满足条件，因为最深的 lca 都可以到达；考虑子树外的路径，如上所述，这个选点是 “往上面尽力白嫖 \(d\) 步” 的结果，即在满足子树内限制下尽量往外走的点了。所以可以等效替代

综上，现在的判定变成了计算 \(u\) 和 \(u\) 子树外的 lca 的距离的最小值和 2d 的关系

还是不大好做，因为可能我们这个选点(u)会变，那岂不是要全部重算（考虑利用信息均摊...不大行

2d 不好判，践行白嫖精神，先把 \(u\) 向上跳个 \(d\) 再说，设这个点叫做 \(v\)

同样，子树内外分别考虑。首先一个大前提就是所有路径都要经过 \(v\) 的子树（本来是和 \(u\) 有交），这个上一个 dfs 序 + 树上差分就结束了。

对于 \(v\) 子树内的路径，现在的问题变成了求解 \(u\) 和 \(v\) 子树内部 \(lca\) 的最远距离，唔？最长路？spfa ？ 。/qd 一棵树要什么最短路算法。。。发现实际上求的就是这些“关键点”的直径 唔？关键点？虚树？ ，这个可以借助两个联通块直径合并的经典结论，上一个 DS

所以就是 树上 \(k\) 级祖先 + 树上差分 + 直径合并 + multiset ，上就完了（这就是你抛弃 \(u\) 的代价！！/yx）

JOISC 2019 day2 两道料理

很有意思的一道题！

naive ：显然，有用的时刻可以表示为 \((x, y)\) 表示做了前 \(x\) 道 \(A\)， 前 \(y\) 道 \(B\)，此时，每一个加分项也可以表示成 \((\le x, \le y)\) 之类的形式。这时候，wyb 突然脑洞，联想到 [ARC101D]Robots and Exits 的建模方式，即看作是从 \((0,0)\) 走到 \((n, m)\) ，每步向上向右，然后越过某一条线会有贡献。

对应到这里，就成了 \(x,y\) 轴上分别竖立这若干根和这根坐标轴垂直的线，点经过这条线就会有贡献。

然后感觉这个两种贡献很难受，不好搞，需要找个方式转化一下....（没有时间思考了/fn/fn/fn 思考时间给得太少）

yysy，想到这里，可以称之为高光时刻了 /hanx

正解：平凡地想到这个建模方式的思路应该是设 \(f(x, y)\) 表示做 \(x\) 道 \(A\)， 前 \(y\) 道 \(B\) 的最大价值，然后通过对 DP 转移方程的观察看出是一个在二维平面上行走的问题，再把方程中的转移条件转化。

最终得到的模型：从 \((0,0)\) 开始往 \((n,m)\) 每步向上向右，平面上撒着若干个点，对于一个红点 \((i, y_i)\)，如果在路径上或者路径上方，有 \(p_i\) 贡献；对于一个蓝点 \((x_i,i)\) ，如果在路径上或者路径下方，有 \(q_i\) 贡献。

注意路径上指的是被路径覆盖。

不好算，简单容斥，先给答案加上 \(\sum p\)， 然后把 \(p_i\) 取负。此时需要算的是在路径下方的红点和在路径上/路径下方的蓝点，不统一。

考虑把红点 向左向上整体平移， 那么此时的在路径上/下方 就对应原来的在路径下方

此时，设 \(f(x, y)\) 表示走到 \(x,y\) 的最大贡献，设 \(sum(x,y)\) 表示 \((x,0\dots y)\) 的总贡献，有

\[f(x,y) = \max(f(x, y - 1), f(x - 1, y) + sum(x - 1, y)) \]

即我们认为拐角处才贡献，不会算重。注意这里 \(sum\) 不一定单调

竭诚观察这个式子， 思考 \(f\) 的值之间的关系。可以看做是先把 \(f(x - 1)\) 贺了一份过来，此时 \(f(x)\) 是单调的。然后在前缀的某些点上挂上一些标记表示对从 \(i\) 开始的所有值加上一个可正可负的数。

既然是单调的，我们可以以差分的视角来看待这个问题 。原 f(x - 1) 差分数组非负。

考虑当前如果加入的是一个正数，会把差分数组上这个位置增加
当前如若加入的是一个负数，对于差分数组当前数 \(d[i]\) 而言，如果 \(d[i] + x < 0\) 被干成了负数，因为对 \(f(x, y - 1)\) 取了 \(\max\)，所以变成 \(0\)；而 \(i + 1\) 位置相当于 \(i - 1\) 的增量是 \(d[i] + d[i + 1]\) ，所以是比较 \(d[i]+d[i+1]\) 和 \(x\)。

所以加入一个负数会使得后面连续的一段总和最多为 \(x\) 的数清零 (最后所有数都为 \(0\) 或有一个数只被减去了一部分)。这个过程可以直接用 set/线段树二分 维护。

更顺畅地得到这个维护差分做法的思路是先考虑暴力的做法
暴力做法需要支持的是区间加、所有数取前缀 max
假设这两种操作是交替的，考虑每次把一段区间 \([l,r]\) 整体抬高 \(h\)，此时由于前缀 max, 需要二分出第一个位置和 \(a[r]\) 的差值大于 \(h\) ；把一段区间整体降低 \(h\) ，那需要二分出来的是那个位置不需要向前面取 \(\max\)
由此，发现我们非常关注差值的变化，所以我们考虑维护差分数组。
由此，引出了线段树上二分的思路。

一共写 + 调 接近 4h，最开始不懂这个怎么才能 set， 然后自己口胡了一个线段树上二分上去，觉得非常科学

然后狂暴乱肝，狂暴输出+画图手模，2h30min 左右总算是过了样例，交上去 49pts, WA

写了一个暴力对拍，总算是发现了问题 /hanx 写完回头看了一眼 set 的写法，发现其实很好懂而且好写/qd

bugs：

• lj 编译器不支持 fread
• 线段树上找到查询区间进一步往里走的时候，不要忘记 pushdown
• query 区间和的时候，写法中存在 \(l, r\) 和 \([L,R]\) 无交的情况，死循环
• 把 \((i,y_i) \to (i - 1, y_i + 1)\) 之后， 可能会大于 \(m\)
• 对于 \(x_i = n\) 的情况，必须贡献 （卡死我了

「C.E.L.U-03」布尔 [solved]

为解决一类具有决策单调性问题提供了一个很好的思路

很容易想到 2-SAT 的建图，由于此处是双向边，所以我们可以直接上并查集维护连通性

可以想到求出 \(f_i\) 表示 \(i\) 第一个不能到的位置，处理出来之后可以倍增处理询问

当然可以暴力加边然后做，这样复杂度是 \(O(n^3)\) ，其中 \(O(n)\) 实际上是判定的复杂度，每次新加入一条边都要把所有的点枚举一遍，判断它的 partner 是否连通了。

但是这样是没有必要的，因为如果存在一对不合法的点，考虑我们这里的连边方式，可以知道每一对点都是不合法的，我们只需要随便判断一个就可以了

瓶颈来到对于加边的枚举，容易发现 \(f\) 是单调不降的，这个可以类似贪心的证明。

需要维护的信息比较复杂，考虑模仿整体二分决策单调性的做法，设 \(solve(l,r,L,R)\) 表示求 \(f_{l\sim r}\)，且答案必在 \(L\sim R\) 内。

保证并查集已经含有 \(l_{r+1\sim L-1}\) 的边，我们有如下几步：

• 计算 \(f_{mid}\)，逐个加入 \(l_{L\sim R}\)，逐个判断
• 递归 \(solve(l,mid,L,p)\)，此时，需要把并查集变成 \(l_{mid + 1,L -1}\)
• 递归 \(solve(mid +1,r,p,R)\)，此时，需要把并查集变成 \(l_{r + 1, p -1}\)

发现这些东西都是我可撤销并查集可以做的，这种好事。

这其实揭示了在贡献不能删除只能撤回（回滚）时，双指针配合决策单调性分治的方法。
—— command block

另外一道使用整体二分 + 可撤销并查集的题目 WD 与地图

既然涉及到可撤销并查集，我们也有了线段树分治 的做法，巨好写

[20220722海亮NOI集训] 传统

给定三个长度为 \(n\) 的序列 \(a, b, v\) ，保证 $b_i \ge a_i $。
有 \(n\) 个物品，第 \(i\) 个物品的价格是 \(a_i\) ，价值是 \(v_i\) 。设用 \(t\) 元能买到的物品的最大价值是 \(f(t)\)
你可以选择一个非空区间 \([l, r]\) ，把区间中的物品的价格从 \(a_i\) 变成 \(b_i\) 。给定正整数 \(k, E\)，你需要使得价格改变之后 \(\frac1k \sum^k_{i=1} f(k) \le E\)
求有多少个合法的区间 \([l, r]\)
\(n, k \le 2\times 10^5, nk \le 10^7\)

妙妙题，依旧是决策单调性的做法，和上一道题差不多

注意到固定 \(l\) ，可行的 \(r\) 的范围是一个后缀，\(r\) 单调。

也是 \(Solve(l, r, L, R)\) 求解区间 \([l, r]\) 的答案在 \([L,R]\) 之中，当前层求取 \(mid = (l + r) / 2\) 的答案

01背包支持增加一个新的物品

每次进入一个 solve 的时候，保证 \([1, min(l, L)]\) 和 \([R + 1, n]\) 都是取 \(a_i\)，保证 \([r + 1, L - 1]\) 取的是 \(b_i\) 即可

特别注意保证 \(b_i\)，这个是保复杂度的东西。一个问题是不能撤销，假设当前做的是完全背包的话，有一个妙妙的思路就是先加入 \(b_i\) 再加入 \(a_i\) 会把最开始的 \(b_i\) 覆盖掉。但是现在是 01 背包，所以只能再开一个数组暂存

考虑求取 \(pos[mid]\)，在 \([L,R]\) 中二分即可。每次二分的时候需要把 \([left,right]\) 遍历一遍来加入 \(a/b\)。这里算出来复杂度看似是 log^2，即有 log 个区间需要二分，每次二分也是 log

但是重点是 log^2 是 log^2，不一定是 nlog^2

考虑我二分过程中，一次二分区间长度砍一半，所以就是 \(L + \frac L2 +\frac L4 + \dots + 1 = 2L - 1\)

所以每一个区间加入 \(O(len)\) 次，总复杂度 \(O(nk\log n)\) 就可以过了

[20220718海亮NOI集训] 数数

时空限制：5s，256 MB
问在 \(m\) 种字符构成，长度为 \(n\)，每种字符个数不超过 \(c_i\) 个的所有字符串中，有多少本质不同的后缀数组。

神仙题，疯狂转化，疯狂改变枚举量

考虑本题中后缀数组的作用，发现仅仅是提供一个对于偏序关系的定义而已

考虑最暴力的做法，枚举字符串，求出 SA。稍微优化一下，可以想到枚举 SA，然后判断这个 SA 是否可行

具体的判断方法是，我们贪心地想使用尽量少的字符集来构造这个 SA。对于 \(S_{sa_i}\le S_{sa_{i + 1}}\)，表现为能取等就取等。取等条件是 \(rk_{sa_i + 1} < rk_{sa_{i + 1} + 1}\)，否则取 \(<\)

此时，我们得到了形如 \(S_{sa_1} = S_{sa_2} < S_{sa_3} = \dots\) 的关系，设第 \(i\) 段相等的段的长度为 \(d_i\)，设有 \(m\) 段

一组 \(d\) 和 \(c\) 合法当且仅当可以把 \(c\) 分成 \(m\) 段，使得 \(c_1+c_2+\dots c_x \ge d_1, c_{x + 1} + \dots c_y \ge d_2\) 之类。比如 \(d=\{4,2,3,1\}, c = \{3,2,4,1,2\}\)，则只能是 \(c_1,c_2\) 用于 \(d_1\)；\(c_3\) 用于 \(d_2\), 然后 \(c_4,c_5\) 用于 \(d_3\) 。留下一个 \(d_4\) 不合法。（可以填 \(=\) 自然可以写 \(<\)）

此时我们有了 \(O(n!)\) 枚举 SA，\(O(n + m)\) 判断的方法

注意到SA 的作用仅仅是提供一个 \(d\)，一个 \(d\) 对应多个 \(SA\)。考虑再次改变枚举顺序，想要直接枚举 \(d\) 。

对于一个 \(d\) 而言，对应的 SA 个数为 \(\binom{n}{d_1, d_2, \dots, d_m}\)。可以理解为随机排列然后有些段内部是没有顺序的（相等）

现在的问题是存在又可以 \(=\) 又可以 \(<\) ，非常不方便和 \(c\) 进行判断，一个考虑是容斥 \(=\)，钦定只有 \(t\) 个 \(<\) ，那么答案大致是：

\[\sum (-1)^t \binom{n}{d_1 + d_2\dots d_x, d_{x+1}+\dots,\dots} \]

考虑 DP 组合意义

设 \(f_{i, j, k}\) 表示使用了 \(c_{1\dots i}\) 去匹配，当前 \(\sum d = j\)， 当前 \(d = k\) 的 \(\frac{1}{len!}\) 的带容斥系数和

• 可以结束一段： \((k + l)! f_{i, j, k}\to f_{i, j + l, 0}\)
• 可以合并两段： \(-f_{i, j, k} \to f_{i, j + l, k + l}\)
• 可以新来一个： \(f_{i, j, k} \to f_{i, j + c_i, k + c_i}\)

对角线前缀和优化即可

没时消

half understand AGC040F Two Pieces 南极洲的冰川 画圈

7.27 自主消化

上午主要在肝昨天的 JOISC 2019 day2 两道料理 。中午和 zqm 以 zqm 的总结为中心玩耍了一小会儿，然后下午一下子就把题调出来了 /hanx

下午写 布尔，非常有意思的题目

还有 2h 左右，准备完善总结之类，想摆了，觉得歌很好听

在找题的时候点进了 gls 的杂题列表，发现好多题一看都是懵的，完全没有印象，说明以前做题的质量实在算不上高。

摆摆摆