[JSOI2011] 柠檬 题解
[JSOI2011] 柠檬 题解
决策单调性+单调栈+二分
学习自:皎月半洒花 十分强大的做法
Statement
给定长为 的序列 ,定义一段区间的价值为 ,其中 表示前 个个数中 的个数
把序列划分为任意多的区间,求最大价值和
Solution
随便列出一个方程, 表示以 为一段的结尾的最大值
wtcl,所以乱猜了一个全局的决策单调性,自己在 xjb 证明的时候居然还觉得是对的,然后给出了一个 的做法, 是分块算贡献
打完才发现根本没有全局决策单调性,GG
一看到题解第一句话就发现自己蠢得一笔。贪心一下,容易发现一个区间的两个端点的颜色必然是相同的,不然调整一下显然更赚,于是题目一下子就好做了很多
其中 表示 前面 的 个数
列完之后没有多想,直接上了一个斜率优化艹过去了
回来看 皎月半洒花神犇 的题解,发现了高级的决策单调性的用法!
从上面那个式子可以看出,对于单个颜色而言,如若 且 优于 ,那么随着 的增加, 会一直优于 ,即单个颜色是有颜色单调性的
一个 naive 的想法产生了,那能不能直接把每一种颜色提出来单独做决策单调性的算法呢?
不行,因为转移式中使用到了 ,颜色不一定对
那么只能混着一起做了,直接使用单调栈把路过的决策记下来,如若新决策比栈顶优秀那么直接干掉
但是问题来了,观察两个决策点 随着 的增长值的变化:
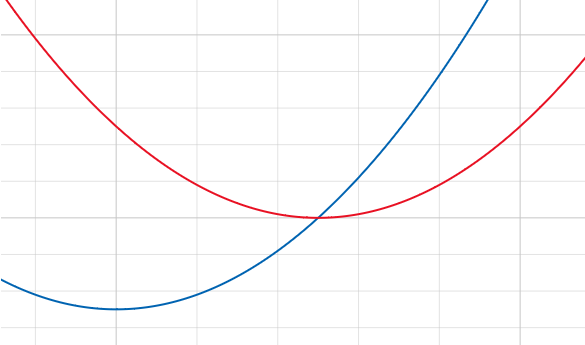
(蓝色 ,红色 )
也就是说,在一段时间里面,可能是 凭着 比较 nb,干爆了 ,但是毕竟 在二次函数背景下长远看更优,所以 又取代了
这样的话,我们上面那个做法就有可能伤及无辜
所以应当怎样判断一个栈顶元素是否应该被清除呢?
考虑 二分 出 比 优秀的起始时间,设为
- 如若 ,即当前的位置,那么显然 成为一个废决策
- 对于新加入的一个决策 ,如若 ,那么 GG
(只有 受伤的世界完成了)
对于第二种情况的理解,可以自行画画图,发现这个式子表现在图像上,就是 被 联合覆盖导致 GG
upd 2022.7.20 其实这个就是决策单调性更本质性的用法
考虑平时的决策单调性,我们使用的方法是维护一个三元组的的队列然后新增决策的时候在队列中二分进行替换
而这道题的不同之处在于,一个决策可能存在先劣后优的趋势,所以需要更具体的分析
这种分析方法的另外一个相对简单的应用 [USACO08MAR]土地征用 Land Acquisition- FlashHu
复杂度
Code
特别小心 对 也是一个决策,所以要先加入新决策然后
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5+5;
const int M = 1e4+5;
char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
int read(){
int s=0,w=1; char ch=getchar();
while(!isdigit(ch)){if(ch=='-')w=-1; ch=getchar();}
while(isdigit(ch))s=s*10+(ch^48),ch=getchar();
return s*w;
}
int a[N],c[N],mp[M],f[N];
vector<int>q[M];
int n;
#define A q[t][q[t].size()-2]
#define B q[t][q[t].size()-1]
int calc(int x,int t){
return f[x-1]+a[x]*t*t;
}
int find(int x,int y){
int res=n+1,l=1,r=n;
while(l<=r){
int mid=(l+r)>>1;
if(calc(x,mid-c[x]+1)>calc(y,mid-c[y]+1))
res=mid,r=mid-1;
else l=mid+1;
}
return res;
}
signed main(){
n=read();
for(int i=1;i<=n;++i)
a[i]=read(),c[i]=c[mp[a[i]]]+1,mp[a[i]]=i;
for(int i=1,t;t=a[i],i<=n;++i){
while(q[t].size()>=2&&find(A,B)<=find(B,i))
q[t].pop_back();
q[t].push_back(i);
while(q[t].size()>=2&&find(A,B)<=c[i])
q[t].pop_back();
f[i]=calc(B,c[i]-c[B]+1);
}
printf("%lld\n",f[n]);
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】