「NOI2020」美食家 题解
最大值矩阵快速幂+倍增
Statement
给定一张 \(n\le 50\) 个点 \(m\le 501\) 条边的有向图，边权 \(w\le 5\)，点有点权 \(c_i\le 52501\)
现在想从 \(1\) 出发，经过恰好 \(T\) 时间（中途不停留），经过一条边消耗边权 \(w\) 时间，回到 \(1\)
无法到 \(1\) 输出 \(-1\) ，否则输出经过点权和的最大值
给出 \(k\le 200\) 个附加条件，即点 \(x\) 在时刻 \(t\) 权值增加 \(y\le 10^9\)
Solution
容易想到设 \(f[u][j]\) 表示在 \(j\) 时刻走到点 \(u\) 的最大值
其中 \(ex[u][j]\) 表示额外权值
看到状态里面有 \(j\) ，那肯定是要上矩阵快速幂的，考虑把 \(c_u\) 这个点权放到边上，\(1\) 号点特殊处理即可
令 \(mp[v][u]=c_u\) ，那么
发现 \(w\) 很小，大喜过望，经由 排队 - 题目 - FZUOJ (fzoi.top) 的启发，知道了可以把 \(u\) 直接拆成 \(5\) 个点即可（一般的，这种拆点矩阵快速幂的方式，只需要关注当前最大的位置的转移即可，其他位置可以理解为仅仅是记录信息，比如在本题中，最开始只需要填写 \(f[x][5]\) 的转移即可，其他的保留信息即可）
那么这长成一个 $\max $ 的样子咋办，借用动态 DP（eg.P5024 [NOIP2018 提高组] 保卫王国) 的思想，我们知道可以重定义矩阵运算
但是还是不知道外面那个 \(ex\) 咋办，GG，我们看题解去！以下学习自：M_sea
发现其实也比较好处理，由于每两个特殊贡献的时间不一样，所以可以先将这些贡献按时间排序。
考虑在相邻两个美食节之间，做一遍普通的DP转移。例如，第 \(j\) 个时间 \(t_j\)，第 \(j-1\) 个时间 \(t_{j-1}\)，则这段的转移：
然后后令 \(dp[t_j][x_j]+=y_j\)，即可。
也就是说，本来，我们是直接乘上一个 \(G^T\) ，但是为了在转移过程中加上特殊贡献，所以我们分成 \(k=200\) 段转移。
这样暴力做 \(200\) 段转移肯定不能过，所以我们借鉴 [NOI Online #3 提高组] 魔法值 的思想，预处理 \(G,G^2,G^4,G^8,\dots\) ，那么对于 \(G^x\) ，就可以倍增地 \(log\) 算值了
所以总复杂度 \(\mathcal{O}((wn)^3\log T+(wn)^2k\log T)\)，小卡常，需要使用 FastIO
Code
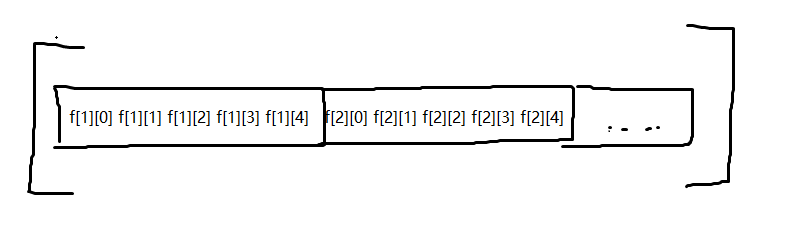
矩阵具体大概长成这样：
#include<bits/stdc++.h>
#define int long long
#define id(x,y) (((x)-1)*5+(y))
using namespace std;
const int inf = 1e18;
const int N = 55;
char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
int read(){
int s=0,w=1; char ch=getchar();
while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
while(isdigit(ch))s=s*10+(ch^48),ch=getchar();
return s*w;
}
bool cmax(int&a,int b){return a<b?a=b,1:0;}
bool cmin(int&a,int b){return a>b?a=b,1:0;}
int c[N],f[N][5];
bool mp[N][N][5];
int n,m,t,K;
struct Line{int u,v,w;}line[N*10];
struct Node{
int t,x,y;
bool operator<(const Node&rhs)const{
return t<rhs.t;
}
}a[N<<2];
struct Matrix{
int n,m;
int mat[N*5][N*5];
Matrix(int _n=5*N-1,int _m=5*N-1):n(_n),m(_m){
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
mat[i][j]=-1e9;//不能直接赋成 -inf(-1e18),运算中会爆 ll
}
Matrix operator*(const Matrix&rhs)const{
Matrix res(n,rhs.m);
for(int i=1;i<=n;++i)for(int j=1;j<=rhs.m;++j)for(int k=1;k<=m;++k)
res.mat[i][j]=max(res.mat[i][j],mat[i][k]+rhs.mat[k][j]);
return res;
}
}A,B,T[33];
void ksm(int x){
for(int i=0;(1<<i)<=x;++i)
if(x>>i&1)A=A*T[i];
}
signed main(){
n=read(),m=read(),t=read(),K=read();
for(int i=1;i<=n;++i)c[i]=read();
for(int i=1,u,v,w;i<=m;++i)
u=read(),v=read(),w=read(),
mp[v][u][w]=1,line[i]=(Line){u,v,w};
for(int i=1;i<=K;++i)
a[i].t=read(),a[i].x=read(),a[i].y=read();
sort(a,a+K+1);
for(int i=1;i<=n;++i)
for(int j=0;j<=4;++j)
f[i][j]=-1e9;
f[1][0]=c[1];
for(int j=1,k=1;j<=4;++j){
if(j==a[k].t)c[a[k].x]+=a[k].y;
for(int i=1;i<=m;++i)if(j>=line[i].w)
cmax(f[line[i].v][j],f[line[i].u][j-line[i].w]+c[line[i].v]);
if(j==a[k].t)c[a[k].x]-=a[k].y,k++;
}
// for(int i=1;i<=n;++i,puts(""))
// for(int j=0;j<=4;++j)
// cout<<max(f[i][j],-1ll)<<" ";
A.n=1,A.m=n*5;
for(int i=0;i<32;++i)T[0].n=T[0].m=5*n;
for(int i=1;i<=n;++i)for(int j=0;j<=4;++j)A.mat[1][id(i,j+1)]=f[i][j];
for(int i=1;i<=n;++i)for(int j=1;j<=4;++j)T[0].mat[id(i,j+1)][id(i,j)]=0;
for(int i=1;i<=n;++i)for(int j=1;j<=5;++j)for(int k=1;k<=n;++k)
if(i!=k&&mp[i][k][j])T[0].mat[id(k,5-j+1)][id(i,5)]=c[i];
for(int i=1;(1<<i)<=t;++i)T[i]=T[i-1]*T[i-1];
// for(int i=1;i<=n*5;++i,puts(""))
// for(int j=1;j<=n*5;++j)
// printf("%2lld ",max(T[0].mat[i][j],-1ll));
int k=1,tim=4;
while(k<=K&&a[k].t<=tim)++k;
while(k<=K){
if(tim<a[k].t-1)
ksm(a[k].t-tim-1),tim=a[k].t-1;
B=T[0];
for(int i=1;i<=n*5;++i)
B.mat[i][id(a[k].x,5)]+=a[k].y;
A=A*B,++k,++tim;
}
if(tim<=t+4)ksm(t+4-tim);
// for(int i=1;i<=n*5;++i,puts(""))
// for(int j=1;j<=n*5;++j)
// printf("%2lld ",max(A.mat[i][j],-1ll));
printf("%lld\n",max(A.mat[1][1],-1ll));
return 0;
}
