[CSP-S 2021] 交通规划题解

对偶图网络流+区间 DP

CCF一到店，所有 OIer 便都看着他笑，有的故意的高声嚷道，“你的题一定又超纲了！”CCF睁大眼睛说，“你怎么这样凭空污人清白……”“什么清白？我去年 CSP T4 啥都不会，被吊着打。”CCF便涨红了脸，额上的青筋条条绽出，争辩道，“题难不能超纲……题难！……出题的事，能算超纲么？

去年的题现在才来补 qwq

还记得考前教练说绝对不可能考网络流，哈哈

考场上不知道在干什么，45 分的 $k=2$ 都不会 qwq，wtcl

严格来说也没有超纲，毕竟代码里面只有最短路和 DP 嘛

Statement

P7916 [CSP-S 2021] 交通规划 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

给定一个 $n\times m(n\times m\le 500)$ 的网格图，边有非负边权。网格图外围有一层 $2n+2m$ 个特殊点，特殊点仅和相邻网格图上的点有连边，最开始边权为 $\rm 0$。 $q(q\le 50)$ 个询问，每个询问给定 $k(\sum k\le 50)$ 个特殊点的对应的非负边权、位置、颜色（黑白），你可以决定网格图上的点的颜色，两个有边相连的点有值为边权的贡献当且仅当两个点颜色不同，最小化贡献和。

Solution

考虑一个 01 变量 $x$，将 $x=0 $ 视为其对应点与源点联通，$x=1$ 视为与汇点联通。那么考虑最小割中每条边的贡献：对于形如 $(S,x,a)$ 的边，当且仅当 $x$ 与汇点联通时这条边才会有 $a$ 的贡献，于是可以将这条边的贡献记为 $ax$ 。同理，形如 $(x,T,a)$ 的边可看成 $a(1-x)$，而形如 $(x,y,a)$ 的边则可看成 $a(1-x)y$。对于某些问题，我们可以将贡献拆成上述三种形式，便可以通过跑最小割求解。

——Bindir0

容易发现转对偶图之后 $k=2$ 就是一个最小割的事情，dij 就可以了（边权非负）

k=2

#include<bits/stdc++.h>
#define id(x,y) ((x)*(m+1)+(y))
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N = 505;

char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
int read(){
    int s=0,w=1; char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
    while(isdigit(ch))s=s*10+(ch^48),ch=getchar();
    return s*w;
}
bool cmin(int &a,int b){return a>b?a=b,1:0;}

struct Edg{
    int nex,to,dis;
}edge[N*N*4];
struct Point{
    int x,p,t;
}node[55];
int head[N*N],pos[N<<2],dis[N*N];
priority_queue<pii,vector<pii>,greater<pii> >q;
vector<pii>Edge[N*N];
int n,m,T,elen;
bool vis[N*N];

void addedge(int u,int v,int w,int op=1){
    if(op)Edge[u].push_back(pii(v,w));
    edge[++elen]=(Edg){head[u],v,w},head[u]=elen;
    edge[++elen]=(Edg){head[v],u,w},head[v]=elen;
    // cout<<u<<" "<<v<<" "<<w<<endl;
}
int dijkstra(int s,int t){
    memset(vis,0,sizeof(vis)),memset(dis,0x3f,sizeof(dis));
    dis[s]=0,q.push(pii(0,s));
    while(q.size()){
        int u=q.top().se; q.pop();
        if(vis[u])continue; vis[u]=1;
        for(int e=head[u],v;v=edge[e].to,e;e=edge[e].nex)
            if(cmin(dis[v],dis[u]+edge[e].dis))q.push(pii(dis[v],v));
    }
    return dis[t];
}

signed main(){
    n=read(),m=read(),T=read();
    for(int i=1;i<n;++i)for(int j=1,x;j<=m;++j)
        x=read(),addedge(id(i,j-1),id(i,j),x);
    for(int i=1;i<=n;++i)for(int j=1,x;j<m;++j)
        x=read(),addedge(id(i-1,j),id(i,j),x);
    for(int i=1;i<=m;++i)pos[i]=id(0,i);
    for(int i=m+1;i<=n+m;++i)pos[i]=id(i-m,m);
    for(int i=n+m+1;i<=n+2*m;++i)pos[i]=id(n,n+2*m-i);
    for(int i=n+2*m+1;i<=2*n+2*m;++i)pos[i]=id(2*n+2*m-i,0);

    while(T--){
        int k=read(),nw=(n+1)*(m+1);
        for(int i=1;i<=k;++i)
            node[i].x=read(),node[i].p=read(),node[i].t=read();
        if(k<=1||node[1].t==node[2].t){puts("0");continue;}
        for(int i=node[1].p;i!=node[2].p;i=i%(2*n+2*m)+1)addedge(pos[i],nw,0,0);
        for(int i=node[2].p;i!=node[1].p;i=i%(2*n+2*m)+1)addedge(pos[i],nw+1,0,0);
        addedge(nw,nw+1,min(node[1].x,node[2].x),0);
        printf("%d\n",dijkstra(nw,nw+1));////
        memset(head,0,sizeof(head)),elen=0;
        for(int x=0;x<(n+1)*(m+1);++x)
            for(auto v:Edge[x])addedge(x,v.fi,v.se,0);
    }
    return 0;
}

naive 的，我们猜想 $k>2$ 是不是直接设一个超级源点，超级汇点就可以了

发现不是很刑，你这样割，把白点割到汇点所属集合里面怎么办

这样做还有一个问题是，因为我们是要先转化对偶图的（直接在原图上跑会 T 飞），而路径可能会交叉，那咋转对偶图

我们考虑把问题转化到 $k=2$ 的情况。

首先，我们顺时针把射线连起来，同时，从某一个特殊点开始，如若 $i+1$ 不是特殊点/颜色和 $i$ 一样，那么我们认为 $i,i+1$ 同属一个连通块，于是大致形成了这样的情况：

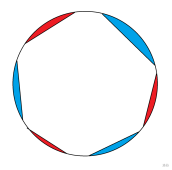
（图源：约瑟夫用脑玩）

容易发现红色数量必然和蓝色数量相同（奇数直接合并在一起）

给出一个结论：将一个红色块和一个蓝色块两两配对跑最短路，再去掉这些最短路对应的原图的边集，那么答案方案就是这些边集权值和

可以说明的是，不用担心路径重复的问题，因为如若重复，那么交换一下配对方式肯定可以干掉重复的路径而且显然更优。

结论的证明可以感性理解一下。最后的答案肯定是长成这个形式，因为我如若有一个割是从某个连通块内部出发的，那显然不是很有用；也不会是路径走到一半就断掉，走一半断掉没有起到分割颜色的作用，不如不走。

具体证明可以看：此处大意是暴力分类讨论。

具体的，由于引入了新点（连通块代表点），可以将相邻连通块之间的权值设为第二个（顺时针）连通块的第一条射线权值（按照上面所述划分连通块方式，这必定是一个特殊射线）

对于连通块内的射线之间，边权 $0$ 好了，以防止这样的情况：

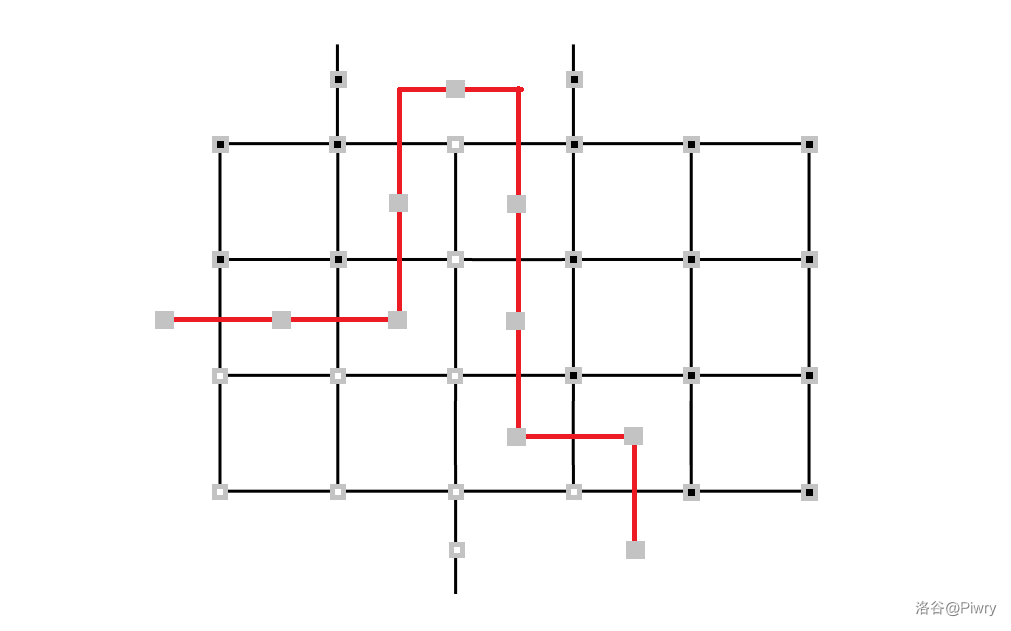
（图源：Piwry，我怎么在到处嫖图 /fn

为了找到最优的配对方式，我们可以执行一个区间 DP 的过程

首先管都不管，跑 $k$ 次最短路，预处理数组 $dis[x][y]$ 表示第 $x$ 个特殊点到第 $y$ 个特殊点的最短路

然后设 $dp[l][r]$ 表示匹配区间 $[l,r]$ 中的点的最小答案，注意这里破环为链

转移：$dp[l][r]=min(dp[l+1][r-1]+dis[l][r],\min \{dp[l][k]+dp[k+1][r]\})$

转移的时候特别注意一定时刻保证使用的 dp 值所代表的区间长度是偶数

所以总复杂度 $O(\sum k (nm)\log (nm)+\sum k^3)$

Code

代码学习自：Piwry

#include<bits/stdc++.h>
#define id(i,j) ((i)*(m+1)+(j))
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
typedef long long ll;
const int N = 5e2+5;
const int K = 55;

char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
int read(){
    int s=0,w=1; char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
    while(isdigit(ch))s=s*10+(ch^48),ch=getchar();
    return s*w;
}
bool cmin(ll&a,ll b){return a>b?a=b,1:0;}
bool cmin(int&a,int b){return a>b?a=b,1:0;}

struct Dijkstra{
    struct Edge{int nex,to,dis;}edge[N*N*4];
    priority_queue<pii,vector<pii>,greater<pii> >q;
    int head[N*N],orihead[N*4*2],orid[N*4*2];
    //双向边两倍，一共 4n 条射线，每条射线像所属连通块连边
    int dis[N*N],vis[N*N];
    int elen,orielen;

    void addedge(int u,int v,int w){
        edge[++elen]=(Edge){head[u],v,w},head[u]=elen;
        edge[++elen]=(Edge){head[v],u,w},head[v]=elen;
        // cout<<u<<" "<<v<<" "<<w<<endl;
    }
    void addedge2(int u,int v,int w){
        orihead[++orielen]=head[u],orid[orielen]=u;
        edge[++elen]=(Edge){head[u],v,w},head[u]=elen;
        // cout<<u<<" "<<v<<" "<<w<<endl;
    }
    void reset(){//卡常嘎嘎嘎，原图上的边重复用
        elen-=orielen;
        while(orielen)
            head[orid[orielen]]=orihead[orielen],
            orielen--;
    }
    void dijkstra(int s){//dijkstra
        memset(vis,0,sizeof(vis));
        memset(dis,0x3f,sizeof(dis));
        dis[s]=0,q.push(pii(0,s));
        while(q.size()){
            int u=q.top().se; q.pop();
            if(vis[u])continue; vis[u]=1;
            for(int e=head[u],v;v=edge[e].to,e;e=edge[e].nex)
                if(cmin(dis[v],dis[u]+edge[e].dis))q.push(pii(dis[v],v));
        }
    }
}graph;
struct Point{int w,p,t;}node[K];
int pos[N<<2],dis[K][K];
ll dp[K<<1][K<<1];
vector<int>vec;
int n,m,T,siz;

signed main(){
    n=read(),m=read(),T=read(),siz=(n+1)*(m+1);
    for(int i=1;i<n;++i)for(int j=1,w;j<=m;++j)
        w=read(),graph.addedge(id(i,j-1),id(i,j),w);//id(i,j) 是对偶图下标
    for(int i=1;i<=n;++i)for(int j=1,w;j<m;++j)
        w=read(),graph.addedge(id(i-1,j),id(i,j),w);
    for(int i=1;i<=m;++i)pos[i]=id(0,i);
    for(int i=m+1;i<=n+m;++i)pos[i]=id(i-m,m);
    for(int i=n+m+1;i<=n+2*m;++i)pos[i]=id(n,n+2*m-i);
    for(int i=n+2*m+1;i<=2*n+2*m;++i)pos[i]=id(2*n+2*m-i,0);//顺时针处理射线位置
    //for(int i=1;i<=2*n+2*m;++i)cout<<pos[i]<<" ";puts("");

    while(T--){
        int k=read(),nw=siz;
        for(int i=1;i<=k;++i)
            node[i].w=read(),node[i].p=read(),node[i].t=read();
        sort(node+1,node+1+k,[](Point x,Point y){return x.p<y.p;});
        // for(int i=1;i<=k;++i)
        //     cout<<node[i].p<<" "<<node[i].w<<" "<<node[i].t<<endl;
        node[k+1]=node[1],vec.clear();
        for(int i=1;i<=k;++i){
            for(int j=node[i].p;j!=node[i+1].p;j=j%(2*m+2*n)+1)
                graph.addedge2(nw,pos[j],0),graph.addedge2(pos[j],nw,0);
            if(i<k)graph.addedge2(nw,nw+1,node[i+1].w),graph.addedge2(nw+1,nw,node[i+1].w);
            else graph.addedge2(nw,siz,node[1].w),graph.addedge2(siz,nw,node[1].w);
            if(node[i].t!=node[i+1].t)vec.push_back(nw);
            nw++;
        }
        if(vec.size()==1)puts("0");//特判 k=1
        else{
            for(auto u:vec){
                graph.dijkstra(u);
                for(auto v:vec)
                    dis[u-siz][v-siz]=graph.dis[v];
            }
            int tmp=vec.size();
            for(int i=0;i<tmp;++i)vec.push_back(vec[i]);

            memset(dp,0x3f,sizeof(dp));
            for(int i=0;i+1<tmp*2;++i)//破环为链
                dp[i][i+1]=dis[vec[i]-siz][vec[i+1]-siz];
            for(int len=4;len<=tmp;len+=2)//注意控制区间长度
                for(int l=0;l+len-1<tmp*2;++l){
                    int r=l+len-1;
                    dp[l][r]=dp[l+1][r-1]+dis[vec[l]-siz][vec[r]-siz];
                    for(int i=l+1;i<=r-2;i+=2)
                        cmin(dp[l][r],dp[l][i]+dp[i+1][r]);
                }
            ll ans=1e18;
            for(int i=0;i-1<tmp;++i)
                cmin(ans,dp[i][i+tmp-1]);
            printf("%lld\n",ans);
        }
        graph.reset();   
    }
    return 0;
}

类似的题目有 CF1368H2 Breadboard Capacity (hard version)，主要的思想都是建出最大流图之后，发现数据范围问题不能直接网络流。所以从最大流=最小割入手，使用最短路/DP 等等求解最小割。

在上面那道题中，使用的方法就是用 DP 做最小割，然后用 DDP 处理动态修改问题。

posted @ 2022-05-06 16:53 _Famiglistimo 阅读(318) 评论(0) 编辑收藏举报

刷新页面返回顶部

lost_heart_hurts

[CSP-S 2021] 交通规划题解

[CSP-S 2021] 交通规划题解

Statement

Solution

Code

公告

lost_heart_hurts

[CSP-S 2021] 交通规划 题解

[CSP-S 2021] 交通规划 题解

Statement

Solution

Code

公告

[CSP-S 2021] 交通规划题解

[CSP-S 2021] 交通规划题解