SAM 学习笔记

集训字符串内容默认大家都会 SAM/SA ，我不会，所以学一下

学完做了几道例题，突然在敲 SAM 板子的时候不知道这个是在干什么，为什么这样干，发现自己对 SAM 的理解不够

所以这里口胡一下，以希可以加强一下对 SAM 的理解

由于全是口胡，所以写得很垃圾而且乱，但是干货满满

请先学习 AC 自动姬或者对自动姬有一些了解

---

SAM ，后缀自动姬，其意义是，从初始状态开始在 SAM 走到某个结束状态，中间的转移会形成原串的一个后缀，并且能够走到所有后缀

那么，在行走过程中，走的是某一个后缀的前缀

所以 SAM 的某一条路径（不一定走完）代表了原串的一个子串

SAM 是一个 DAG，是满足上述要求的点数最小的 DAG

在不考虑点数最小的限制，我们可以考虑 $O(n^2)$ 暴力在 Trie 树上插入原串的所有后缀，这样形成的 trie 其实叫做后缀 Trie

你随便尝试了了一个字符串，发现这样很蠢，容易发现这个 Trie 树的结构是可以压缩的

也就是说某一些边可以并在一起，某一些节点可以并在一起

于是某一位神仙想到，我说，endpos 集合相同的子串可以合并成一个状态

比如在字符串中 $aababa$ ，$ba$ 和 $aba$ 的 $endpos$ 都是 $\{4,6\}$ ，我们把他看成一个状态

我们称这个状态叫做 endpos 等价类

现在的问题是这样是否能够优化点数，为什么这样可以表达所有子串和如果可行，如何快速构造

探索一下 endpos 的性质

• 一个子串只属于一个 endpos（显然）

• 子串 $s$ 和子串 $t$ 同属同一个 endpos 集合，当且仅当 $s,t$ 中较短的串是另外一个串的后缀而且短串每个结束位置都是长串的结束位置（定义）

  上面好像很废，再稍微多想一下：$|s|\le |t|$

  $$\begin{cases} endpos(t)\subseteq endpos(s),&s\ is\ a\ suffix\ of\ t\\ endpos(s)\cap endpos(t)=\varnothing,& otherwise \end{cases}$$

• 一个 $endpos(u)$ 等价类中的串互为后缀且长度连续

  如若类中只有一个子串，显然成立，设类中最长子串长度 $len(u)$ ，最短 $minlen(u)$

  显然最短子串是最长子串的后缀，在最短子串的前面不断向最长串补齐字符，过程中的串都在类中且长度连续

• $enpos$ 等价类只有 $O(n)$ 个

  容易发现对于一个子串而言，他的真后缀的 endpos 集合大小大于等于他的 endpos 大小

  所以我们可以认为每次在一个子串前面加字符会砍掉原来的 endpos 的一部分

  比如 $aababa$ ，$ab$ 的 endpos 为 $\{3,5\}$ ; $aab$ ，endpos $\{3\}$; $bab$ ，endpos $\{5\}$

  加不同的字符显然会得到不交的 endpos 集合（性质2）

  不管加什么字符，得到的 endpos 集合必然是原集合的子集（性质2）

  当然，我们在前面也可以加多个字符，有时候只加一个的话 endpos 不会变

  在我的理解中，一个 endpos 的代表子串是他最长的子串，因为这样在加一个字符后 endpos 一定会变

  回到这个性质，我们认为空串的 endpos 为 $\{1,2,3,\dots,n\}$ ，每次加字符可以认为是在划分集合同时保留原集合，总分割次数不会超过原集合大小，所以最多有 $O(n)$ 个 endpos 等价类

  我们发现这样划分的方式使得 endpos 类之间存在了某种父子关系，嫖一张图：$aababa$

  ![image-20220309103000250](

  （https://www.luogu.com.cn/blog/Kesdiael3/hou-zhui-zi-dong-ji-yang-xie）

  我们把这个树叫做 $parent\ tree$ ，注意图上仅标注了每一个类最长的子串

• 在 $parent\ tree$ 上，$minlen(u)=len(fa)+1$

  我们定义后缀链接(link) 就是从儿子跳到父亲，即把 $minlen(u)$ 的第一个字符抠掉

  其实跳 link 就是不断跳自己后缀的过程

我们已经解答了第一个问题，即是否能够优化点数

下一个问题是为什么这样可以表达所有子串

回顾我们的想法：把这些 endpos 类作为 SAM 的状态

我们发现这个问题其实是和 endpos 类之间的转移有关的，即和 SAM 的构造有关的

考虑普通的状态转移（endpos 的转移）

在原串末尾加上一个新字符c，则产生了一个新的状态

因此一个状态能通过一个字符转移到另一个状态，下面，我们通过构造的方式，可以验证所有字串都可以被表达。

记为 $ch[u][x]$ ，即状态 $u$ 可以通过加 $x$ 字符转移到 $ch[u][x]$

考虑如何在 endpos 类之间建立转移边，我们采用 增量法，假装我已经对于原串的前 $n-1$ 个字符建立了 SAM ，我考虑我加入第 $n$ 个点的影响

空子串的 endpos 为 1 号节点

称前 $n-1$ 个字符构成的子串的 endpos 为 last

连边规则如下，加入字符 $x$（注意，以下连边、划分状态的一个重要的基本点就是，要使得划分出的每一个状态符合 endpos 的性质，主要是要符合所有 endpos 一样的都放在一起，且如果 endpos 不同那么一定不能放在一起）

1. 新建状态 $p$ 代表前 $n$ 个字符形成的字符串的 endpos 。从 last 开始跳 link ，如果从 last 到空子串的路径上 $\forall endpos(u) ,ch[u][x]==0$ ，那么把这些 $ch[u][x]=p$ ，$link[p]=1$

   注意我们 SAM 要满足的条件是“从初始状态开始在 SAM 走到某个结束状态，中间的转移会形成原串的一个后缀，并且能够走到所有后缀”，所以我们沿转移边走到原有的 SAM 的结束点，得到的是前 $n-1$ 个字符的所有后缀

   由于没有任何一个子串以 $x$ 结束，也就是 $x$ 是SAM中没有出现过的，因此所有后缀的 endpos 一定都是 $n$ ，直接把这些转移到 $p$ 即可。对于 $p$ 而言，它的 endpos 集合比较无敌，你无论怎么删它的前缀，它的 endpos 不变，所以直接将 link 连 1

   我跳 link 的意义，就是枚举所有以 $c$ 为结尾的子串的意义

2. 在从 last 开始跳 link 的路径上 $\exist endpos(u),ch[u][x]=q \wedge len[u]+1==len[q]$

   也就是当前后缀在原串中不仅仅出现 $n$ 那里一次

   因为 $len[u]+1==len[q]$ ，所以 $q$ 中的串全都是 $u$ 中的串 $+x$ 得到的。

   那么对应的后缀全都在q里，因此直接 $link[p]=q$ ，直接跳出即可，即 $q$ 是不和 $p$ 在同一 endpos 集合的最长后缀

   之所以是最长，因为我在跳 link 的时候已经“尽力”了，注意我每次都是从 last 起跳

   同时可以考虑一下 $len$ 是否符合：可以发现，对于 $q$ 中的点，$endpos$ 相比于加入 $x$ 之前多了一个 ${n}$ 且原本 endpos 集合肯定非空；而对于当前的一些后缀 $[i,n]$ 而言，他们的 endpos 只有 $\{n\}$。那么到底是哪些 $i$ 只有 ${n}$ 呢，容易发现其实就是 $[len[q]+1,len[p]]$ 对应的部分。

3. 在从 last 开始跳 link 的路径上 $\exist endpos(u),ch[u][x]=q \wedge len[u]+1<len[q]$

   说明 $q$ 不配（不能保证 endpos 不同的不能放在一起这个性质），我们需要捏一个 $cur$ 出来，使得 $cur$ 有 $q$ 的所有信息，而且 $len[cur]=len[u]+1$ ，变成情况 2（显然 $cur$ 的 endpos 和 $q$ 的 endpos 已然不同，多了 $n$ 的部分）

   显然 $cur$ 代替 $link[q]$ ，成为 $q$ 第一个不在同一个 endpos 的最长后缀

   于是我们 $link[q]=link[p]=cur$（这里也说明了一个问题，就是当我在不断跳转移边的时候，当前得到的字串并不能认为就是 $len[u]$ 对应的串）

   然后把之前所有转移到 $q$ 的边都移植到 $cur$ 即可。

我们可以通过图来理解上述过程，以 $aababa$ 为例子建立 SAM

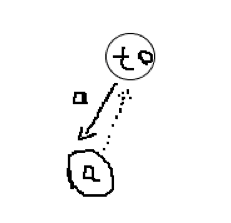
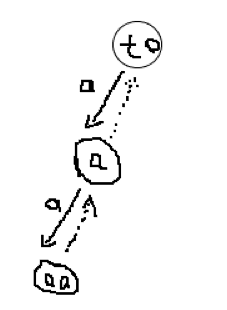
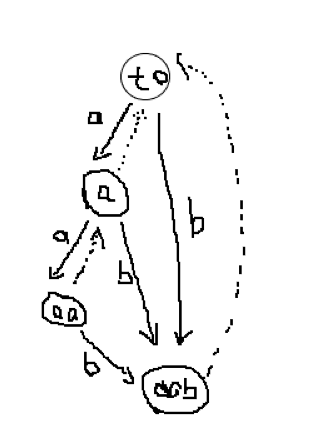
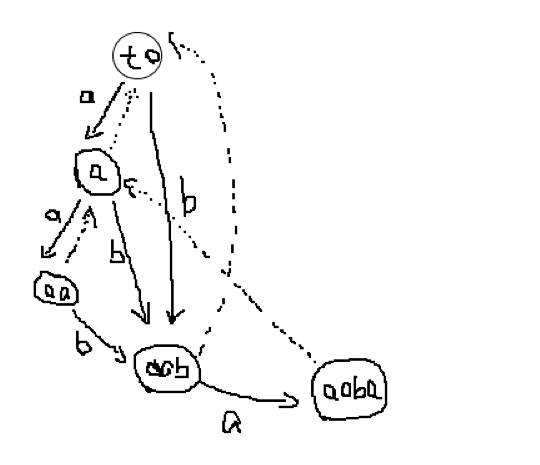
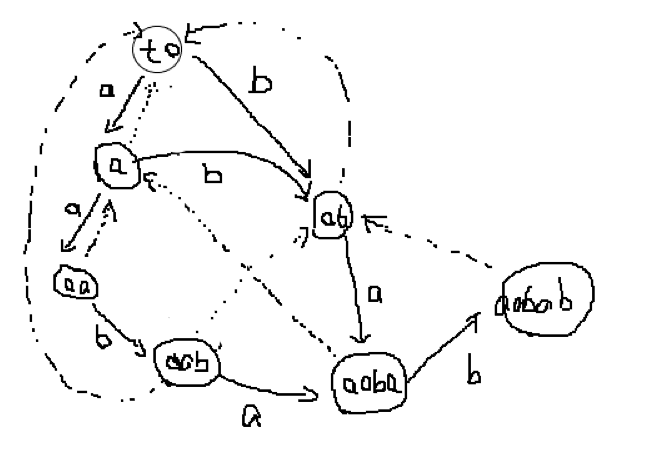
（图丑）

剩下一个 aababa 的情况留作练习（

在明白上述构造过程之后，我们容易理解下述代码

注意下面的 p 和 las 和上文的意义有所出入

void insert(int x)
{
    int p = las; // 旧状态
    node[las = ++cnt].len = node[p].len + 1;
    for (; p && !node[p].ch[x]; p = node[p].link)
        node[p].ch[x] = las;
    if (!p)
        return node[las].link = 1, void();
    int q = node[p].ch[x];
    if (node[q].len == node[p].len + 1)
        return node[las].link = q, void();
    int cur = ++cnt;
    memcpy(node[cur].ch, node[q].ch, sizeof(node[q].ch));
    node[cur].link = node[q].link, node[cur].len = node[p].len + 1;    
    node[q].link = node[las].link = cur;
    for (; node[p].ch[x] == q; p = node[p].link)
        node[p].ch[x] = cur;
}

到此，按理说应该继续写 SAM 的应用，但本文的最初目的是加强理解，这个目的现在也许已经达到了，所以撒花

---

upd 2023.8.16

可以发现，设 $pos[i]$ 表示插入了前缀 $s[1,i]$ 的 $p$，也就是将 $s[1,i]$ 扔进自动机走到的状态。那么前缀 $i$ 和前缀 $j$ 的 lcs 就是 parent 树上 $len[lca(pos[i],pos[j])]$，因为每次跳 link 实际上取消了一个尽量短的不匹配的前缀。

那么可以发现 反串的 SAM 的 parent tree 就是后缀树。因为后缀树上两个节点的 $len[lca]$ 代表的是两个后缀的 lcp。

而我们又知道在后缀树上 dfs 可以得到 SA，所以可以用 SAM 构造 SA！

当然可能 SA 不能构造 SAM，因为 SAM 的转移边 trans 也许比较难泵。