[ZJOI2016]大森林 题解

LCT

对 LCT 有了更深的理解

参考 FlashHu

Statement

有 $n$ 棵树，初始各有 $1$ 个编号为 $1$ 的节点，称它们为生长节点。

$m$ 个操作，$3$ 种之一：

• $0\ l\ r$ 将 $[l,r]$ 区间内的树的生长节点加一个编号相同的儿子
• $1\ l\ r\ x$ 修改 $[l,r]$ 区间内的树生长节点为 $x$（没有该节点的树忽略此操作）
• $2\ x\ u\ v$ 询问第 $x$ 棵树上两点的距离（保证存在）

$n\le 10^5,m\le 2\times 10^5$

Solution

显然我们有 $O(n^2 \log n)$ 的暴力 LCT 做法，但是好像空间有点着不住

最初的想法是说容易发现其实很多边都是一样的，所以我们可以尝试数据结构优化建图之类的

经过思考之后发现不会，其问题在于 $1$ 操作过后的区间关系没有特殊关系（相离/包含）

然后看题解（ 注意到一个询问只关心在左端点在 $x$ 之前的修改，且没有强制在线的说法，考虑离线

于是我们有了这样的基础思想：从 $1$ 到 $n$ 枚举每棵树，每次只考虑相邻两棵树之间的差异，只需要在前一棵树的基础上快速地得到这棵树的形态就可以了

考虑一个操作 $1\ l\ r\ x$ 的影响，先假装所有树都是一样的

发现其造成的差异只有 $l-1$ 和 $l$ ，$r$ 和 $r+1$ 这两个位置，知道

第 $l$ 棵树是第 $l-1$ 棵树把这个 $1$ 操作以后 原来生长节点上的所有子树全部转而接到 $x$ 上。

第 $r+1$ 棵树是第 $r$ 棵树把这些子树接回来

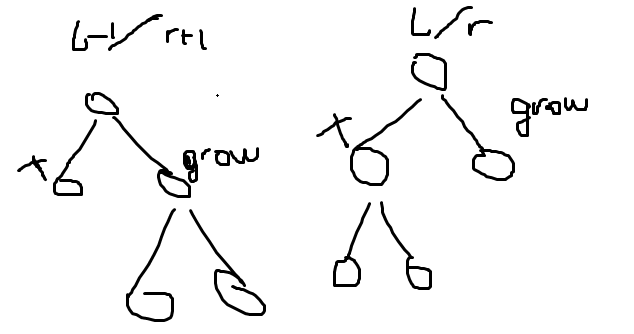
图丑爆了（

现在的问题在于如何把这些子树快速地扔过去，考虑给他一个虚点

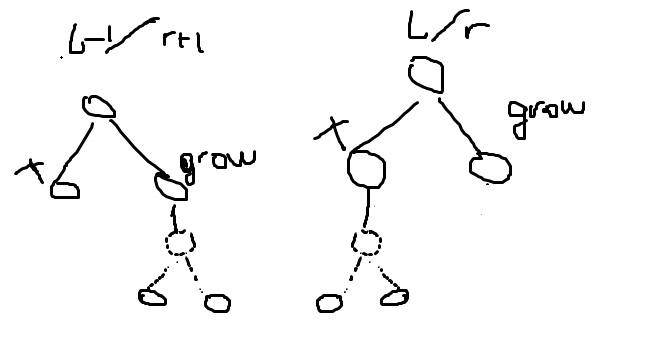
也就是说，我们每次在进行 $1$ 操作的时候，我们给他新建一个虚点 $img$ ，

最开始 $link(img,grow)$ ，然后让 $grow^{\prime}=img$ ，之后就直接挂在 $img$ 上

然后到 $l-1$ 和 $l$ 的时候，我们让 $img$ 改成连 $x$

把每个操作拆成两个端点，以端点为第一关键字，原时间顺序为第二关键字排序，再从左到右一个个处理即可

现在考虑处理过程中的询问

容易想到设实点权 $1$ ，虚点权 $0$ ，然后只需要 $makeroot(u),access(v),splay(v)$ 三连即可？

发现好像不是很行，因为固定根 $1$ 我们 $makeroot(u)$ 可能会改掉一些父子关系

同时，考虑到两个实点的路径上有可能存在虚点，而虚点可能包含了非路径上的信息，我们考虑树上差分

假装都会 LCT 求 LCA，那么答案就是 $siz[u]+siz[y]-2\times siz[lca]$ ，注意这些 $siz[tmp]$ 一定都要 $access(tmp)$ 之后取用

时间复杂度 $O(n\log n)$

Code

#include<bits/stdc++.h>
#define ls(rt) t[rt].ch[0]
#define rs(rt) t[rt].ch[1]
#define swap(x,y) x^=y^=x^=y
#define min(x,y) ((x)<(y)?(x):(y))
#define max(x,y) ((x)>(y)?(x):(y))
using namespace std;
const int N = 2e5+5;

char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
int read(){
    int s=0,w=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
    while(isdigit(ch))s=s*10+(ch^48),ch=getchar();
    return s*w;
}

struct Tree{int f,val,siz,ch[2];}t[N];
struct Item{int pos,tim,x,y;}item[N];
int gl[N],gr[N],pos[N],ans[N];
int n,m,grow,cnt,img,tim,tot;

void pushup(int rt){t[rt].siz=t[rt].val+t[ls(rt)].siz+t[rs(rt)].siz;}
bool check(int rt){return ls(t[rt].f)!=rt&&rs(t[rt].f)!=rt;}
bool identity(int rt){return rs(t[rt].f)==rt;}
void rotate(int rt){
    int f=t[rt].f,ff=t[f].f,op=identity(rt),ch=t[rt].ch[op^1];
    t[rt].f=ff,t[rt].ch[op^1]=f,t[ch].f=f,t[f].ch[op]=ch;
    if(!check(f))t[ff].ch[identity(f)]=rt;
    t[f].f=rt,pushup(f),pushup(rt);
}
void splay(int rt){
    while(!check(rt)){
        int f=t[rt].f;
        if(!check(f))
            rotate(identity(f)==identity(rt)?f:rt);
        rotate(rt);
    }
}
int access(int rt,int p=0){
    for(;rt;p=rt,rt=t[rt].f)
        splay(rt),rs(rt)=p,pushup(rt);
    return p;
}
void cut(int rt){access(rt),splay(rt),ls(rt)=t[ls(rt)].f=0;}
inline void link(int p,int q){t[p].f=q;}
/*
本题中的 link 比较特殊，既不需要 makeroot ，也不用 splay
考虑 link 使用场景，无非是新建的点（虚点）或者离线求解时的转移
新建点的点显然就是根了，而另外一种，因为我们已经 cut 了，所以也是根
所以直接把父亲设为 q 即可
*/

signed main(){
    n=gr[1]=read(),m=read();
    t[1].val=t[1].siz=pos[1]=gl[1]=cnt=1;
    //pos[1] 点 1 的编号，gl/r 记录修改操作，假装初始有一个操作 0 1 n
    //cnt 记录实点的个数，img 记录虚点的个数
    link(img=grow=2,1);
    for(int i=1,op,l,r,x;i<=m;++i){
        op=read(),l=read(),r=read();
        if(op==0)
            link(pos[++cnt]=++img,grow),
            t[img].val=t[img].siz=1,//实点权 1
            gl[cnt]=l,gr[cnt]=r;
        if(op==1){
            x=read(),l=max(l,gl[x]),r=min(r,gr[x]);
            if(l>r)continue;
            link(++img,grow);//虚点权 0
            item[++tot]=(Item){l,i-m,img,pos[x]},//保证修改在询问前
            item[++tot]=(Item){r+1,i-m,img,grow};
            grow=img;
        }
        if(op==2)
            x=read(),item[++tot]=(Item){l,++tim,pos[r],pos[x]};
    }
    // 此时，LCT 维护出了如果没有任何 1 操作时的树并准备好了所有虚点
    sort(item+1,item+1+tot,[](Item a,Item b)
        {return a.pos==b.pos?a.tim<b.tim:a.pos<b.pos;});
    for(int i=1,x,y,l,tm;x=item[i].x,y=item[i].y,tm=item[i].tim,i<=tot;++i)
        if(tm>0)
            l=access(x),splay(x),ans[tm]+=t[x].siz,
            l=access(y),splay(y),ans[tm]+=t[y].siz,
            access(l),ans[tm]-=t[l].siz<<1;//致命 access，调了亿会儿
        else cut(x),link(x,y);
    for(int i=1;i<=tim;++i)
        printf("%d\n",ans[i]);
    return 0;
}