CF1416F Showing Off
Statement
一开始有一张 \(n\times m\) 的网格图，一开始，每个节点 \((i,j)(1\le i\le n,1\le j\le m)\) 会连恰好一条有向 边，指向 \((i,j+1),(i,j-1),(i+1,j),(i-1,j)\) 其中一个（当然，这个指向的点要在网格上，不能到边界外）。一开始每个点带有一个点权 \(w_{i,j}\ge 1\)，记 \(S_{i,j}\) 为 \((i,j)\) 在图上能到达的点的 \(w\) 之和。 现在你只知道 \(n,m,\{S_{i,j}\}\)，请求出一种合法的 \(w_{i,j}\) 和连边方案，使得 \(\{S_{i,j}\}\) 正确。
\(1\le nm\le 10^5,S_{i,j}\in[2,10^9]\cap \N\)
Solution
显然，我们最后连成的图会是一个基环内向树森林
由于这是一个网格图，黑白染色容易发现我们的基环必然是一个偶环，且基环上面所有点的 \(S\) 相同
我们可以贪心地把基环拆成若干个二元环，这样更容易满足 \(S\) 相同的要求
显然，基环树上，父亲的 \(S\) 小于儿子
现在等价于这样的问题：每个点可以直接成为自己旁边某个 \(S\) 小于自己的点的儿子，或者和自己旁边某个和自己 \(S\) 相同的点组成二元环，且必须选其中之一。
一个点显然不能连向大于它的点。
假如一个点旁边的点都 \(\ge\) 它，那么它必须选择一个权值相同的点
一个点 \((i,j)\) 如果旁边有小于自己的点 \((x,y)\)，那么它可以不选择权值相同的点。
注意到假若一个点周围所有的点的值都大于它，那么它无法连边，即无解。
即要求做一个二分图匹配（黑白染色，黑点为左部点，白点为右部点），但某些点必须在匹配里
这里的处理方式是跑一个有源汇上下界可行流，对于一个必须匹配的黑点 \(u\) ，那么从源点向 \(u\) 连边 \([1,1]\) ，\(u,v\) 连边 \([0,1]\) ，\(v\) 连边汇点 \([1,1]\)
可惜这样的问题在于，它最后形成的图不是二分图，大概长这样：
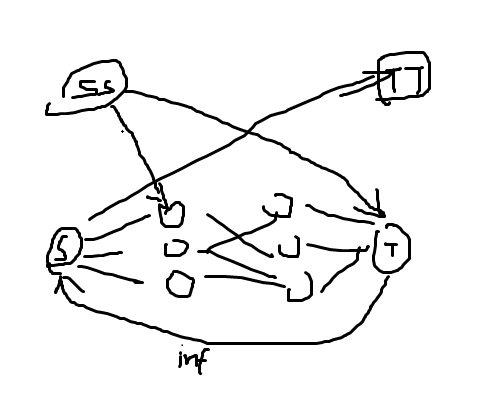
所以它不是二分图，所以复杂度是没有保证的，但是本题比较良心，没有卡，可以冲
\(\textcolor{balck}{\text{p}}\textcolor{red}{\text{\_b\_p\_b}}\) 给出了这样一个 trick：
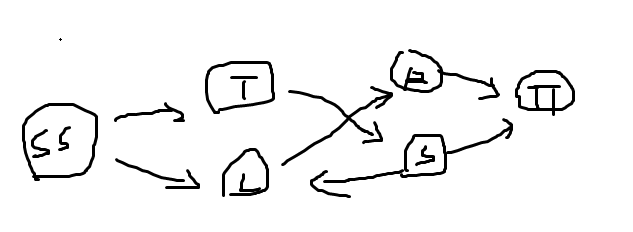
做一个新图 \(G\)。考虑拎出必须匹配的左部点和所有右部点，跑二分图匹配，如果没有完备匹配说明无解，否则视为在 \(G\) 上，每个左部点向它匹配的右部点连一条边。
然后拎出所有左部点和必须匹配的右边点，类似地做，在 \(G\) 上，每个右部点向它匹配的左部点连一条边。
此时发现在 \(G\) 上，每个点的度数至多为 \(2\)，所以只有环和链。
对于环，发现全都是偶环（二分图），隔一条边取一条边作为匹配边，显然环上的每个点都在匹配里了。
对于链，从链开头那条边开始，隔一条边取一条边作为匹配边（比如 ，\(1\to2\to3\to4\) 就取 \((1,2),(3,4)\)
这样如果是偶链的话是可以的，可是奇环的话链最后一个点不在匹配内
仔细思考发现最后一个点其实并不是必须选择的点（不然它就有出边），所以不用管。
这样跑两次二分图匹配就可以得到一个可行的匹配了，复杂度 \(O(nm\sqrt{nm})\)
Code
这里给出网络流爆冲的代码
#include<bits/stdc++.h>
#define id(x,y) ((x-1)*m+y)
using namespace std;
const int N = 2e5+5;
char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
int read(){
int s=0,w=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
while(isdigit(ch))s=s*10+ch-'0',ch=getchar();
return s*w;
}
struct Edge{int nex,to,dis;}edge[N<<2];
int head[N],cur[N],dep[N],S[N],w[N],U[N<<3],V[N<<3];
char op[]={'L','R','U','D'},Ud[N<<2],Vd[N<<2],C[N];
int dx[]={0,0,-1,1},dy[]={-1,1,0,0};
int T,n,m,s,t,ss,tt,cnt,elen,give,rec;
queue<int>q;
void addedge(int u,int v,int w){
if(!w)return ;//
edge[++elen]=(Edge){head[u],v,w},head[u]=elen;
edge[++elen]=(Edge){head[v],u,0},head[v]=elen;
U[elen]=ss;
}
void addedge(int u,int v,int L,int R){
addedge(ss,v,L),addedge(u,v,R-L),addedge(u,tt,L),give+=L;//在差网络上操作
}
bool bfs(){
memset(dep,0,(cnt+1)*4);
dep[ss]=1,q.push(ss);
while(q.size()){
int u=q.front(); q.pop();
for(int e=head[u],v;v=edge[e].to,e;e=edge[e].nex)
if(!dep[v]&&edge[e].dis)dep[v]=dep[u]+1,q.push(v);
}
return dep[tt]!=0;
}
int dfs(int u,int flow){
if(u==tt)return flow; int res=0;
for(int&e=cur[u],v;v=edge[e].to,e;e=edge[e].nex)
if(dep[v]==dep[u]+1&&edge[e].dis){
int tmp=dfs(v,min(flow,edge[e].dis));
edge[e].dis-=tmp,flow-=tmp;
edge[e^1].dis+=tmp,res+=tmp;
if(!flow)return res;
}
return res;
}
void Dinic(){
while(bfs())
memcpy(cur,head,(cnt+1)*4),
rec+=dfs(ss,1e9);
}
signed main(){
T=read();
while(T--){
n=read(),m=read(),elen=1,give=rec=0;
cnt=id(n,m),s=++cnt,t=++cnt,ss=++cnt,tt=++cnt;
for(int i=1;i<=cnt;++i)head[i]=0;
for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)S[id(i,j)]=read();
for(int i=1;i<=n;++i)for(int j=1,l;l=1,j<=m;++j){
for(int k=0;k<=3;++k){
int x=i+dx[k],y=j+dy[k];
if(x<1||x>n||y<1||y>m)continue;
if(S[id(x,y)]<S[id(i,j)])
l=0,C[id(i,j)]=op[k],w[id(i,j)]=S[id(i,j)]-S[id(x,y)];
//这里的实现是直接先取了而不连边，防止找不到匹配
if(S[id(x,y)]==S[id(i,j)]&&((i^j)&1))
addedge(id(i,j),id(x,y),1),
U[elen]=id(i,j),V[elen]=id(x,y),
Ud[elen]=op[k],Vd[elen]=op[k^1];
//这里 U[elen]=id(i,j) 和 addedge 中的 U[elen]=ss 联动，来区分掉 (s,id(i,j))（下面的连边）
}
if((i^j)&1)addedge(s,id(i,j),l,1);//下界 l
else addedge(id(i,j),t,l,1);
}
addedge(t,s,1e9),Dinic();
if(give!=rec){puts("NO");continue;}//流出流入不相同，说明存在一个点所有旁边的点的 S 都比它大
for(int i=3;i<=elen;i+=2)if(U[i]!=ss&&edge[i].dis)//这里遍历的是反向边
C[U[i]]=Ud[i],C[V[i]]=Vd[i],w[U[i]]=1,w[V[i]]=S[U[i]]-1;
puts("YES");
for(int i=1;i<=n;++i,puts(""))for(int j=1;j<=m;++j)printf("%d ",w[id(i,j)]);
for(int i=1;i<=n;++i,puts(""))for(int j=1;j<=m;++j)printf("%c ",C[id(i,j)]);
}
return 0;
}
