FWT 学习笔记
FWT 学习笔记
想尽量讲得本质一点。
首先有一个引出问题叫做 集合幂级数
其中，\(opt\) 是集合的并交补运算，而 \(i,j,k\) 也都是集合的意思
当我们把 \(i,j,k\) 看成二进制表示，那么集合中的每一个元素的选/不选对应二进制的 \(1/0\) ， \(opt\) 变成了 \(or,and,xor\) 的一种
所以问题变成了这样：给定两个长度为 \(2^n\) 的序列 \(a_i,b_i\) （不够长用 \(0\) 补全），求出一个序列 \(c\) ，满足 \(\forall i,c_i=\sum_{j \ opt\ k=i}a_jb_k\)
这个时候我们可以使用，FWT ，\(\text{Fast Walsh-Hadamard Transform}\) ，快速沃尔什变换。
FFT
发现 \(fwt\) 和 \(fft\) 的英文很像，所以我们考虑，类似的思路
关于 \(fft\) ，我们有一个经典思路是：（图源：pyb 的 ppt)
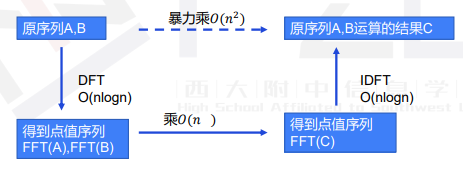
其中，我们能做到 \(O(n\log n)\) 的 \(DFT\) 的原因在于我们有两个重要操作叫做 奇偶分段 蝴蝶变换 ，也就是说我们把原来的东西进行分治的操作后可以 \(O(1)\) 的合并回去，\(O(n\log n)\) 的 \(IDFT\) 在于一个 \(w\) 的性质的应用，我们不妨尝试把这样的思想套进 FWT
记住上图！
FWT
现在我们有这样的目标：找到一种变换 \(FWT\) ，使得
其中，\(\times\) 表示对应位相乘，然后通过 \(FWT(C)\) 复原 \(C\)
显然，我们的 FWT 应该是对于原序列的一种线性组合，即某一项只是若干个原多项式中的若干项的若干倍的和
因为我们本来的 \(c_i\) 就是数个 \(a_jb_k\) 的和，而 FWT 是对应位相乘，如果其出现原多项式某几项的乘积，那么显然 GG
所以显然有的是 \(FWT(A+B)=FWT(A)+FWT(B)\)
这里不妨约定一些记号:
$ 𝐴 = 𝑎_𝑖 ,𝐵 = 𝑏_𝑖 , 𝐶 = 𝑐_𝑖 $
$ 𝐴 + 𝐵 = 𝑎_0 + 𝑏_0, 𝑎_1 + 𝑏_1,\dots $
$ 𝐴 − 𝐵 = 𝑎_0 − 𝑏_0, 𝑎_1 − 𝑏_1,\dots$
$ 𝐴\oplus𝐵 = \sum_{𝑖⨁𝑗=0} 𝑎_𝑖 ∗ 𝑏_𝑗 , \sum_{𝑖⨁𝑗=1} 𝑎_𝑖 ∗ 𝑏_𝑗 ,\dots$
默认所有的数列都有 \(2^n\) 项，即可以理解为集合元素个数有 \(𝑛\) 个
$ 𝐴_0$ 代表数列 \(𝐴\) 的前 \(2^{𝑛−1}\) 项，即最高位（第一个）不选的所有集合，\(𝐴_1\) 代表数列 \(𝐴\) 中的后 \(2 ^{𝑛−1}\) ，即最高位（第一个）选的所有集合
FWTor
假设现在我们的 \(opt\) 就是 \(or\) ，下面简记 \(A|B=\sum_{j|k=i} a_jb_k\)
下面讲得可能有点小乱
FWT
总体想法是仿照 FFT ，考虑一个递归的形式构造出 FWT
显然，当 \(n=0\) 的时候，\(FWT(A)=A\)
下面讨论 \(n>0\) 的情况，我们首先考虑奇偶分段，假装我们已经知道了 \(FWT(A_0),FWT(A_1)\)
于是，一个粗略的 FWT 出现了： \(FWT(A)=Merge(FWT(A_0),FWT(A_1))\)
\(Merge\) 表示直接拼接，xjb 举一个例子：\(Merge(998,244)=998244\)
我们知道 \(FWT(C)\) 需要等于 \(FWT(A)\times FWT(B)\)
还知道 \(C_0=A_0B_0\) ,$ C_1=A_0B_1+A_1B_0+A_1 B_1$
发现上面那个显然不靠谱，我们对应位相乘后，只会得到 \(FWT(C_0)=FWT(A_0)FWT(B_0),FWT(C_1)=FWT(A_1)FWT(B_1)\) 这样一个错误。
也就是说后半部分还需要有 \(FWT(A_0)\) 的信息甩进去，所以：（这里不妨将 FWT 当成一个神秘的抽象函数）
（回顾 \(+\) 的记号：$ 𝐴 + 𝐵 = 𝑎_0 + 𝑏_0, 𝑎_1 + 𝑏_1,\dots $）
可是这样还是有问题呀，这样对应位相乘，好像会多一个 \(FWT(A_0)FWT(B_0)\) 项的贡献出现在 \(FWT(C_1)\) 中
但值得注意的是， \(FWT(C)\) 并不一定需要就是 \(C\) 了，我们不妨将这个问题交给 \(IFWT\) 处理，
至少我们这里保证了信息是完全的，并且符合我们心目中奇偶分段和蝴蝶变换的要求
也就是说像这样给出来后，IFWT 有操作空间，并且 FWT 时间的确是 \(n\log n\)
当然，我们还需要保证 \(FWT(A)\times FWT(B)=FWT(C)\)
这里采用类似数学归纳法的方式证明，思路来自 pyb 的 ppt ，
即假设已知 \(FWT(A_0)\times FWT(B_0)=FWT(C_0),FWT(A_0)FWT(B_1)+FWT(A_1)FWT(B_0),FWT(A_1)FWT(B_1)=FWT(C_1)\) ，那么
小心 \(Merge\) 的括号打的位置
第一个等号：按 FWT 定义展开
第二个等号：按 \(\times\) 定义对应位相乘
第三个等号：利用归纳法得到的结论
第四个等号：把 \(A_0B_0\) 理解成 \(A^{\prime}_0\) , \(A_0B_1+A_1B_0+A_1B_1\) 理解成 \(A^{\prime}_1\)
第五个等号：前文在定义 Merge 的后面一点点所述：
还知道 \(C_0=A_0B_0\) ,$ C_1=A_0B_1+A_1B_0+A_1 B_1$
所以我们归纳证明了 \(FWT(A)\times FWT(B)=FWT(C)\)
IFWT
（小剧场）
FWT: 至高无上的 IFWT ！吾交给汝一个使命：干掉 $FWT(A) \times FWT(B) $ 之后出现在 \(FWT(C_1)\) 中的 \(FWT(A_0B_0)\) 项！主不需要它！
IFWT：（心里mmp：彩笔 FWT）哈哈哈！看我容斥！
（突然发现自己好智障）
直接给出来：
其中传入的 \(A\) 是经历了 \(FWT\) 的产物，小证一手：
\(FWT(A)\times FWT(B)=FWT(C_0)+FWT(C_0+C_1)\)
所以：
\(IFWT(FWT(C_0)+FWT(C_0+C_1))=Merge(IFWT(FWT(C_0)),IFWT(C_0+C_1-C_0))=Merge(IFWT(FWT(C_0)),IFWT(FWT(C_1)))=C\)
FWT 的本质
我们考虑 FWT 的代码怎么写，这里再嫖一张 pyb 的 ppt
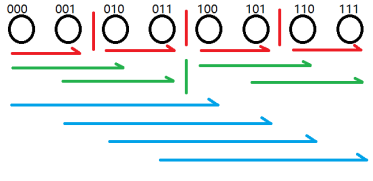
发现 \(FWT\) 做的事情就是不断地让箭头的起点加到箭头的终点，按照红绿蓝的顺序一层一层地加，可以有代码：
void FWT(ll *A){
for(int i=2;i<=N;i<<=1) //i 线段长度
for(int p=i>>1,j=0;j<N;j+=i)//j 哪一个部分
for(int k=j;k<j+p;++k) //k 嫖取信息
A[k+p]+=A[k];
}
我们仔细观察这些箭头究竟都干了什么：
对于 \(111\) 而言，它嫖走了 \(110,101,011\) 的信息
对于 \(110\) 而言，它嫖走了 \(101,010\) 的信息
对于 \(101\) 而言，它嫖走了 \(100,001\) 的信息
对于 \(100\) 而言，它飘走了 \(000\) 的信息
你发现了吗？也就是说，每个位置获取的是它二进制少掉一个 \(1\) 后的位置的信息
而在获取这些少掉了 \(1\) 的位置的信息之前，这些少掉了 \(1\) 的位置也获取了它们所需要的信息，所以，我们刚刚不是说 \(FWT\) 可以看成一个“抽象函数”吗，它的“解析式”其实长这样：
\(FWT(A)_i\) 表示 \(FWT(A)\) 的第 \(i\) 项，这里之所以用 \(\subseteq\) 是因为 FWT 本身其实就是在解决“集合幂级数”。
可以带入 \(FWT(A)\times FWT(B)\) 验证一下看是不是就是 \(FWT(C)\)
所以，我们也可以从另外一个角度去证明 FWT 的时间复杂度，即是 \(\sum_{0}^{1<<n}popcount(i)=n2^{n-1}\)
上面给出 \(FWT\) 的代码，其实很容易写出 \(IFWT\) 的代码：
void IFWT(ll *A){
for(int i=2;i<=N;i<<=1)
for(int p=i>>1,j=0;j<N;j+=i)
for(int k=j;k<j+p;++k)
A[k+p]-=A[k];//唯一不同点
}
从代码逻辑的直观感受来看，如果我 FWT 的枚举顺序是 \(i=2...N\)，那 IFWT 的顺序是不是应该从 \(i=N...2\) 才对？
正确性可以这样理解，FWT 本质是线性变化，所以每一个二进制其实挺独立的，也就是满足交换律。（没有必要是从低位到高位做，也可以是任意顺序做，只是这样写比较方便）
我们甚至也可以是随便点定一个排列 \(p\)，然后按照排列 \(p\) 的顺序做。
更为直观的说明是，如果把每一个数字看成是一个 \(F_2^n\) 空间的向量，每一个二进制位代表某一个维度的坐标，那么上面实际上做的就是高维前缀和。而高维前缀和自然可以随便钦定枚举维度的顺序，然后每次 \(0\to 1\)。
所以，我们容易把它整合起来：
void FWT(ll *A,int op){
for(int i=2;i<=N;i<<=1) //i 线段长度
for(int p=i>>1,j=0;j<N;j+=i)//j 哪一个部分
for(int k=j;k<j+p;++k) //k 嫖取信息
A[k+p]+=op*A[k];
}
上面从类似 FFT 的构造线性变化的角度出发，通过一点人类智慧，构造出了点值对应的形式，并证明了这样做是合法的。
但同时我们也发现 FWTor 其实就是高维前缀和的形式，而 IFWTor 就是高维差分，那么，我们能不能直接从高维前缀和/差分的角度来理解这样做 or 卷积的正确性呢？
我们考虑这个高维前缀和的形式：\(F(S)=\sum _{T\subseteq S} f(T)\)
我们说，与之对应的高维差分：\(f(S)=\sum _{T\subseteq S} (-1)^{|S \backslash T|}F(T)\) 其实本质就是容斥原理：
考虑我们的高维前缀和实际上解决的是这样的问题：对于两个不同的组合对象，从对象 1 中选出 \(S\) 的方案数为 \(f(S)\) ，从对象 2 中选出 \(S\) 的方案数是 \(g(S)\) ，我们想要计算的是 \((f*g)(S)=\sum _{T_1\cup T_2 = S}f(T_1)g(T_2)\) 的值
发现实际上能产生贡献的 \((T_1,T_2)\) 需要满足如下条件：
- \(T_1\subseteq S,T_2 \subseteq S\)
- \(\forall x\in S , s.t. x\in T_1 \cup x\in T_2\)
发现第一个条件是比较喜欢的，因为实际上它意味着所有在 \(T\) 中的元素都在 \(S\) 中，限制比较强烈
而第二个条件涉及到一个 \(or\) 的问题，比较麻烦，我们考虑把这个条件容斥掉
条件的否定是： \(\exist x\in S ,s.t. x\notin T_1 \and x\notin T_2\)
考虑枚举 \(S^{\prime }\) 使得 \(\exist x\in S^{\prime}\) 满足上述条件，考虑此时 \(T_1,T_2\) 满足的条件，有
所以：\(f∗g\) 为 \(F⋅G\) 的高维差分，那么 并卷积的高维前缀和为 \(F⋅G\)，即 \(FWTor(f*g)=F·G\)，\(IFWT(F·G)=f*g\)，而 \(F=FWT(f),G=FWT(g)\)。于是，我们从组合容斥的角度，说明了 FWT 的正确性，并了解了其高维前缀和/差分的本质。
下面是题外话，我们可以同样以这样 高维前缀和/差分的思想 去理解莫比乌斯反演，去理解 \(\mu\) 到底是咋搞出来的。
莫比乌斯反演：
若 $g=1*f $ ，构造函数 \(\mu\) ，使得 \(1*\mu = \in\) ，有 \(f=\mu *g\)
写开：\(g(n)=\sum _{d|n} f(d)\)
考虑使用多元组来表示一个数，对于一个 \(n=\prod p_i^{a_i}\) ，我们使用 \((a_1,a_2,\dots ,a_r)\) 来表达
重定义 \(\subseteq\) 符号表示对于两个二元组 \((a_i) ,(b_i)\) ，若 \(\forall i, a_i\le b_i\) ，那么 \((a_i)\subseteq (b_i)\)
那么，可以表示成： \(g(S)=\sum _{T\in S} f(T)\) ，其实就是高维前缀和
所以对应的反演形式，也就是 \(f(n)=\sum _{d|n} \mu (\frac nd)g(d)\) ，可以看做是高维差分 \(f(S)=\sum _{T\subseteq S} (-1)^{|S\backslash T|}g(T)\) ，而对应的 \(\mu(n/d)=(-1)^{|S|-|T|}\)
所以我们得以了解 \(\mu\) 的构造思路！
想象现在我们在做二维差分 ,\(a(i,j)=s(i,j)-s(i-1,j)-s(i,j-1)+s(i-1,j-1)\) ，系数都长成这样：
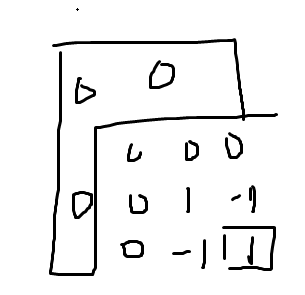
同理，考虑在刚刚所提到的表示法之下的系数，以 \(x=2^i 3^j\) 为例子
\(a(x)=s(x)-s(x/2)-s(x/3)+s(x/6)\) ，对应的 \(\mu(1)=1,\mu (2)=-1,\mu(6)=1,\mu(合数)=0\)
由此：
FWTand
懒得写啦！所以直接摆式子
注意到从某种意义上来说，\(and\) 和 \(or\) 是类似的，以为
\(0|0=1,0|1=1,1|0=1,1|1=1\)
\(0\&0=0,0\&1=0,1\&0=0,1\&1=1\)
void FWT(ll *A,int opt){
for(int i=2;i<=N;i<<=1)
for(int p=i>>1,j=0;j<N;j+=i)
for(int k=j;k<j+p;++k)
A[k]+=A[k+p]*opt;
}
类似上方对于 FWTor 的组合阐述，通过 Jzzhu and Numbers 这道题，我们也可以对 FWTand 做组合阐述。
现在有若干组合对象，\(f_{1,\dots n}(s)\) 分别表示从这 \(n\) 个组合对象里面选出集合 \(s\) 的方案数，求有多少种选 \(s_{1\dots n}\) 的方案，使得 \(And_{i=1}^n s_i=0\)。
方法是容斥，假如我求出了 \(g[i]\) 表示 \(And_{i=1}^n\) 的 \(ppc\ge i\) 的方案数，那么 \(ans=g[0]-g[1]+g[2]\dots\)，（其实就等价于 IFWTand，只不过把 ppc 相同的先加在一起了）
\(g[i]\) 的求法是容易的，只需要求出 \(h[s]\) 表示 \(s\subseteq And\) 的方案数，等价于对于每一个组合对象，都有 \(s\subseteq s_i\)。那么这个其实也就是 FWTand 转成点值然后对应位置相乘。
那么就做完了。
使用一点更为多项式的阐述：
所以这道题的做法就是先在 \(\phi(mod)\) 下用 FWT 把 \(2\) 的幂次做出来，然后带入上式。
FWTxor
其实 FWTxor 的推导过程才和 FFT 是最像的，怎么说呢？
显然有 \(C_0=A_0B_0+A_1B_1\),\(C_1=A_0B_1+A_1B_0\)
FFT 的蝴蝶变换叫做：
FWTxor 直接套用：
然后你发现 \(FWT(A)\times FWT(B)=Merge(FWT(A_0B_0+A_1B_1+A_0B_1+A_1B_0),FWT(A_0B_0+A_1B_1-A_0B_1-A_1B_0))\)
然后你发现前半部分多了 \(A_0B_1+A_1B_0\) ，后面部分需要多了 \(A_0B_0+A_1B_1\) 而且还需要变个号
所以你灵光一现，如此构造出了 IFWT:
\(IFWT(A)=Merge(IFWT(\dfrac{A_0+A_1}2),IFWT(\dfrac{A_0-A_1}2))\)
然后你发现好像是解决了
void fwtxor(int *f,int op){
for(int i=2;i<=len;i<<=1)
for(int p=i>>1,j=0;j<len;j+=i)
for(int k=j;k<j+p;++k){
int x=f[k],y=f[k+p];
f[k]=(x+y)%mod,f[k+p]=(x-y+mod)%mod;
if(op==-1)(f[k]*=inv2)%=mod,(f[k+p]*=inv2)%=mod;
}
}
然后你开始探究 FWTxor 的本质（“解析式”）
然后你懵逼了
然后你上网看了一下：
然后你尝试探究如何从 FWT 的递推式得到它，
然后你发现你想不明白，但是模拟一下它就是对的，于是你有上网一通乱找，你找到了 pyb‘s ppt 的参考文献
（其实一言以蔽之，考虑在 \(F_2\) 下的乘法其实就是 \(ppc(i&j)\)，所以可以从 FFT 为什么对理解 FWT 为什么对）
当你看完了巨佬的文章，你开始尝试自己推导：
这个时候你又知道这样一个式子：
其中 \(U\) 代表某一个大小为 \(2^n\) 的全集，\(W\) 是随便自己给定了一个集合
它的正确性是很显然的，当 \(W\) 不为空的时候，显然会出现一些 \(-1\) ，从而使得这个 \(\sum\) 的值小于 \(2^n\)
当且仅当 \(W\) 为空集的时候，才会使得这个 \(\sum=2^n\)
然后，你利用这个式子，进行你的推导
你发现你的推导还需要一点东西，所以你来证明这个：
其中 \(s_i\) 是某个集合，\(T\) 是某个集合。
首先，我们来证明 \(x=2\) 的情况，即：\(|i\cap (j\oplus k)|\equiv|i\cap j|+|i\cap k|\pmod 2\)
（注意，下面没有采用原博客所使用的方法）
我们直接把集合看成二进制（反正上面的文章也一直把集合和二进制在混用qwq) ，下面简记 \(popcount\to ppc\)
即证明 \(ppc(i\&(j\oplus k))\equiv ppc(i\&j)+ppc(i\&k)\pmod 2\)
（突然发现由于写了太多，导致上面出现了奇怪的人称变化）
设 \(z=i\&(j\oplus k),x=i\&j,y=i\&k\) ，接下来分类讨论，对于二进制每一位，都有：
- \(x\) 当前位为 \(0\) ，\(y\) 当前位为 \(0\) 。那么要么是 \(i\) 没有当前位，要么是 \(j,k\) 均没有当前位，所以 \(z\) 当前位也是 \(0\)
- \(x\) 当前位为 \(0\) ，\(y\) 当前位为 \(1\) 。那么肯定是 \(j\) 没有当前位，\(i,k\) 均有当前位，所以 \(z\) 当前位也是 \(1\)
- \(x\) 当前位为 \(1\) ，\(y\) 当前位为 \(0\) 。那么肯定是 \(k\) 没有当前位，\(i,j\) 均有当前位，所以 \(z\) 当前位也是 \(1\)
- \(x\) 当前位为 \(1\) ，\(y\) 当前位为 \(1\) 。那么肯定是 \(i,j,k\) 均有当前位，\(z\) 当前位为 \(0\) ，在 \(mod\ 2\) 意义下依旧满足
所以现在我们已经证明了 \(x=2\) 的情况，容易发现 \(n>2\) 的情况可以看成 \(n=2\) 的情况，解决
所以我们现在继续我们的推式子大业：
顺理成章的，我们知道了：
！！！
「CF662C」 Binary Table
CF662C Binary Table - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
延续做一道黑题写一篇题解的传统，我们直接把题解写在这里面
Statement
有一个 \(n\) 行 \(m\) 列的表格，每个元素都是 \(0/1\) ，每次操作可以选择一行或一列，把 \(0/1\) 翻转，即把 \(0\) 换为 \(1\) ，把 \(1\) 换为 \(0\) 。请问经过若干次操作后，表格中最少有多少个 \(1\) 。
\(n\leq 20,m\leq 10^5\)
Solution
注意到 \(𝑛\) 很小
容易得到暴力算法：暴力枚举第 \(𝑖\) 行是否翻转，这样每一行的状态就已确定，对于每一次完整的行翻转后，取每一列 \(0/1\) 个数较小的贡献即可。（因为每一列也可以翻转）
时间复杂度是 \(𝑂(𝑚 ⋅ 2^𝑛 )\) ，我们考虑优化掉这个 \(m\)
显然行的操作我们可以状压为 \(𝑥\)，（二进制为 \(1\) 的位表示那一行要翻转）
每一列的的状态值也可以压缩：
- 用 \(𝐴[𝑖]\) 表示在原表列中， \(𝑖\) 这个状态数量
- 用 \(𝐵[𝑖]\) 表示 \(𝑖\) 这个状态最小 \(1\) 的个数（即 \(\min(popcount(i), n-ppc(i)\))
当确定了行的操作为 \(x\) ，那么所有状态为 \(i\) 的列的贡献为：\(A[i]B[i\oplus x]\)
令 \(j=i\oplus x\) ，那么 \(x=i\oplus j\)
所以 \(ans_x=\sum_{i\oplus j=x}A[i]B[j]\) ，直接上 FWT 即可
复杂度：\(O(\max(n2^m,nm))\)
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = (1<<21);
const int M = 1e5+5;
char s[25][M];
int a[N],b[N];
int n,m,ans=1e18;
void fwtxor(int *f,int op){
for(int i=2;i<=(1<<n);i<<=1)
for(int p=i>>1,j=0;j<(1<<n);j+=i)
for(int k=j;k<j+p;++k){
int x=f[k],y=f[k+p];
f[k]=x+y,f[k+p]=x-y;
if(op==-1)f[k]/=2,f[k+p]/=2;
}
}
signed main(){
scanf("%lld %lld",&n,&m);
for(int i=1;i<=n;++i)scanf("%s",s[i]+1);
for(int i=1,k;k=0,i<=m;++i,a[k]++)
for(int j=1;j<=n;++j)k=k<<1|(s[j][i]-'0');
for(int i=0,t;i<(1<<n);++i)
t=__builtin_popcount(i),b[i]=min(t,n-t);
fwtxor(a,1),fwtxor(b,1);
for(int i=0;i<(1<<n);++i)a[i]*=b[i];
fwtxor(a,-1);
for(int i=0;i<(1<<n);++i)ans=min(ans,a[i]);
printf("%lld\n",ans);
return 0;
}
子集卷积
写不动了！！
https://www.luogu.com.cn/problem/P6097
所谓子集卷积，听着很高级，其实也就那样（就最基本的而言），好像有叫做集合占位幂级数什么的
它用来处理求出这样一个 \(c\)：
我们很容易处理第一个限制 \(i \cap j=k\)，直接 FWTand 即可。
对于第二个限制 \(i \cap j=\varnothing\Leftrightarrow |i|+|j|=|i\cap j|\)，所以我们不妨再开一维记录集合中的元素个数
也就是说设 \(f_{i,j} = a_j[|j|=i],g_{i,j}=b_j[|j|=i]\)，把他们卷起来，\(h_{i,j}=\sum_{k=0}^i \sum_{l|r=j}f_{k,l}g_{i-k,r}\)
最后的答案即为： \(c_i=h_{|i|,i}\) ，因为 \(popcount(i)+popcount(j)\ge popcount(i|j)\) ，所以相等的时候取到的就是正确的值
（即 \(|S|+|T|=|S|T|+|S\&T|\) )
#include<bits/stdc++.h>
using namespace std;
const int N = 1<<21;
const int mod = 1e9+9;
int read(){
int s=0,w=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
while(isdigit(ch))s=s*10+ch-'0',ch=getchar();
return s*w;
}
int a[21][N],b[21][N],c[21][N];
int n,len;
void fwt(int *f,int op){
for(int i=2;i<=len;i<<=1)
for(int p=i>>1,j=0;j<len;j+=i)
for(int k=j;k<j+p;++k)
(f[k+p]+=op*f[k])%=mod;
}
signed main(){
n=read(),len=1<<n;
for(int i=0;i<len;++i)a[__builtin_popcount(i)][i]=read();
for(int i=0;i<len;++i)b[__builtin_popcount(i)][i]=read();
for(int i=0;i<=n;++i)fwt(a[i],1),fwt(b[i],1);
for(int i=0;i<=n;++i)
for(int j=0;j<=i;++j)
for(int k=0;k<len;++k)
(c[i][k]+=(long long)a[j][k]*b[i-j][k]%mod)%=mod;
for(int i=0;i<=n;++i)fwt(c[i],-1);
for(int i=0;i<len;++i)printf("%d ",(c[__builtin_popcount(i)][i]+mod)%mod);
return 0;
}
所谓集合占位幂级数，是这样的形式：
扩展：https://www.luogu.com.cn/blog/user7035/zi-ji-juan-ji-ji-ji-gao-ji-yun-suan （我不会，等我长大后再学习）
[WC2018] 州区划分
WC2018 州区划分 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
延续做一道黑题写一篇题解的传统，我们直接把题解写在这里面
Statement
由于原题面已经概括得很好了，所以这里直接贴图:
\(n\leq 21,m\leq n^2/2,p\le 2 ,w_i\le 100\)
Solution
容易考虑状压 DP，设 \(f[i][j]\) 表示划分了 \(i\) 个州，选出的城市的集合为 \(j\) 的贡献，那么
其中，\(sum[s]\) 表示集合 \(s\) 的 \(w\) 的和，\(chk[s]\) 表示集合 \(s\) 是否可以独立成州
所谓独立成州的条件其实可以转化为 图不连通/存在奇度数点，我们容易在 \(O(2^nm)\) 左右的时间暴力预处理出 \(sum,chk\)
设 \(g[k]=sum[k]chk[k]\) ，那么：
发现后面的那一坨其实就是子集卷积，所以复杂度 \(O(n^22^n)\) 解决
Code
#include<bits/stdc++.h>
#define int long long
#define ppc(x) __builtin_popcount(x)
using namespace std;
const int mod = 998244353;
const int N = 22;
char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
int read(){
int s=0,w=1; char ch=getchar();
while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
while(isdigit(ch))s=s*10+(ch^48),ch=getchar();
return s*w;
}
int u[N*N],v[N*N],w[N],fa[N],deg[N],inv[(1<<N)+5];
int f[N][(1<<N)+5],g[N][(1<<N)+5];
int n,m,p;
bool vis[N];
void input(){
n=read(),m=read(),p=read();
for(int i=1;i<=m;++i)u[i]=read(),v[i]=read();
for(int i=1;i<=n;++i)w[i]=read();
}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
bool merge(int u,int v){
u=find(u),v=find(v);
return u==v?0:fa[u]=v;//////////////
}
int ksm(int a,int b){
int res=1;
while(b){
if(b&1)res=res*a%mod;
a=a*a%mod,b>>=1;
}
return res;
}
void preparation(){
for(int i=0,sum,cnt,flag;sum=cnt=flag=0,i<(1<<n);++i){
for(int j=1;j<=n;++j)fa[j]=j,vis[j]=false,deg[j]=0;
for(int j=0;j<n;++j)if(i&(1<<j))vis[j+1]=true,sum+=w[j+1],cnt++;
for(int j=1;j<=m;++j)if(vis[u[j]]&&vis[v[j]])
merge(u[j],v[j])&&(cnt--,1),deg[u[j]]++,deg[v[j]]++;
flag|=cnt!=1,cnt=0;
for(int j=1;j<=n;++j)cnt+=(deg[j]&1);
flag|=cnt!=0,g[ppc(i)][i]=flag*ksm(sum,p);
inv[i]=ksm(ksm(sum,mod-2),p);
}
}
void fwtor(int *f,int op){
for(int i=2;i<=(1<<n);i<<=1)
for(int j=0,p=i>>1;j<(1<<n);j+=i)
for(int k=j;k<j+p;++k)(f[k+p]+=(op*f[k]+mod)%mod)%=mod;
}
void work(){
for(int i=0;i<=n;++i)fwtor(g[i],1);
f[0][0]=1,fwtor(f[0],1);
for(int i=1;i<=n;++i){
for(int j=0;j<i;++j)//j!=i
for(int k=0;k<(1<<n);++k)
(f[i][k]+=f[j][k]*g[i-j][k]%mod)%=mod;
fwtor(f[i],-1);
for(int j=0;j<(1<<n);++j)
f[i][j]=(ppc(j)==i)*(f[i][j]*inv[j]%mod);
if(i^n)fwtor(f[i],1);
}
}
void output(){
printf("%lld\n",f[n][(1<<n)-1]);
}
signed main(){
input();
preparation();
work();
output();
return 0;
}
「CF1034E」Little C Loves 3 III
Statement
给定 \(n\) 和长度为 \(2^n\) 的数列 \(a_{0},a_{1}...a_{2^n-1}\) 和 \(b_{0},b_1...b_{2^n-1}\)，保证每个元素的值属于$ [0,3]$
生成序列 \(c\)，对于 \(c_i\)，有：
\(c_i=\sum_{j|k=i,j\&k=0} a_j\times b_k\)
求 \(c_{0},c_1...c_{2^n-1}\)，答案对 \(4\) 取模。
\(n\le 21\)，时限 \(\rm 1s\)
Solution
显然，暴力 \(O(n^22^n)\) 的子集卷积不可过，考虑利用 \(\bmod 4\) 的性质
普通的，子集卷积为了取到正确的值，采用的方法可以理解为 DP 多设一维状态 \({|S|}\) ，使得我们加入了 \(z^{|S|}\) 这一项
这里，我们让 \(a_S=a_S\times 4^{|S|},b_T=b_T\times 4^{|T|}\) （鬼知道是怎么想到的！）
用 FWT 求出 \(c\) 后，\(x^{|S|}\) 项系数对 \(4^{|S|+1}\) 取模，再除以一个 \(4{|S|}\) 即可
解释：
集合占位幂级数是这样的形式： \(\sum_S (f_S z^{|S|}x^S+\sum_{i>|S|}\sigma_{i,S}z^ix^S)\) 其中 \(z\) 的取值是任意的， $\sigma $ 一般都取 \(\rm 0\) ，\(\sigma\) 意义是在于可能会在 \(S\) 位置瞎 jb 转上一些不计入答案的贡献
而当我们把 \(z\) 取到 \(\rm 4\) ， \(\bmod 4^{|S|+1}\) 干掉了后面那个 \(\sum\) ，除 \(4^{|S|}\) 相当于还原
于是这样快乐 FWT 即可，\(O(n2^n)\)
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
char s[1<<21|5],t[1<<21|5];
int f[1<<21|5],g[1<<21|5];
int n;
void fwt(int *f,int op){
for(int i=2;i<=(1<<n);i<<=1)
for(int p=i>>1,j=0;j<(1<<n);j+=i)
for(int k=j;k<j+p;++k)f[k+p]+=op*f[k];
}
signed main(){
scanf("%lld%s%s",&n,s,t);
for(int i=0;i<(1<<n);++i)f[i]=(s[i]&15ll)<<(__builtin_popcount(i)<<1);fwt(f,1);
for(int i=0;i<(1<<n);++i)g[i]=(t[i]&15ll)<<(__builtin_popcount(i)<<1);fwt(g,1);
for(int i=0;i<(1<<n);++i)f[i]*=g[i]; fwt(f,-1);
for(int i=0;i<(1<<n);++i)putchar(f[i]>>(__builtin_popcount(i)<<1)&3|48);
return 0;
}
完结撒花！！！！✿✿ヽ(°▽°)ノ✿
