[BZOJ 4727]Turysta 题解
Statement
Turysta - 黑暗爆炸 4727 - Virtual Judge (vjudge.net)
Solution
显然,这是一张竞赛图,即有向完全图,竞赛图有这样的性质:
- 竞赛图必有哈密顿路径
- 竞赛图的强连通分量中必有哈密顿回路
首先我们考虑证明第一条性质,使用归纳法构造
显然,一个点可以视为一条哈密顿路径
假设我们现在有一条长度为 \(n\) 的哈密顿路径 \(u_1,u_2,\dots,u_n\),此时,对于一个不在路径上的点 \(v\),它与路径的关系有这样几种:
-
指向 \(u_1\) ,新路径: \(v\to u_1\to u_2\to \dots\)
-
被 \(u_n\) 指向,新路径:\(u_1\to u_2\to\dots \to u_n\to v\)
-
找到第一个 \(x\) 满足 \(v\) 指向 \(u_x\) ,新路径: \(u_{x-1}\to v\to u_x\)
显然,\(x!=1\) ,且此时 \(x=n\) 必然满足条件
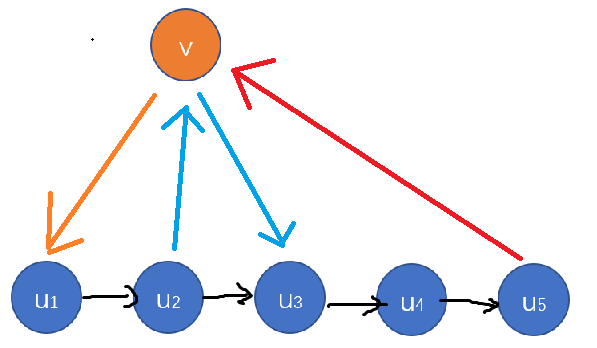
那么现在我们得到一条长度为 \(n+1\) 的哈密顿路径
然后考虑证明第二条性质,仍然采用归纳法
显然,一个点可以视作一条哈密顿回路
假设我们现在有一条长为 \(n\) 的哈密顿回路,\(u_1\to u_2\to \dots \to u_n\to u_1\) ,此时,对于一个不在回路,但在哈密顿路径上点 \(v\) ,它与路径的关系有这样几种;
- 指向 \(u_1\) ,直接扩展 $ \to u_n\to v\to u_1\to\dots $
- 找到第一个 \(x\) 满足 \(v\) 指向 \(u_x\) ,新路径: \(u_{x-1}\to v\to u_x\)
- \(v\) 不指向环中任何一个点,那么一定能找到后续哈密顿路径上一个点 \(w\) 满足 \(w\) 指向环上某一个点(不然不满足强连通条件)。
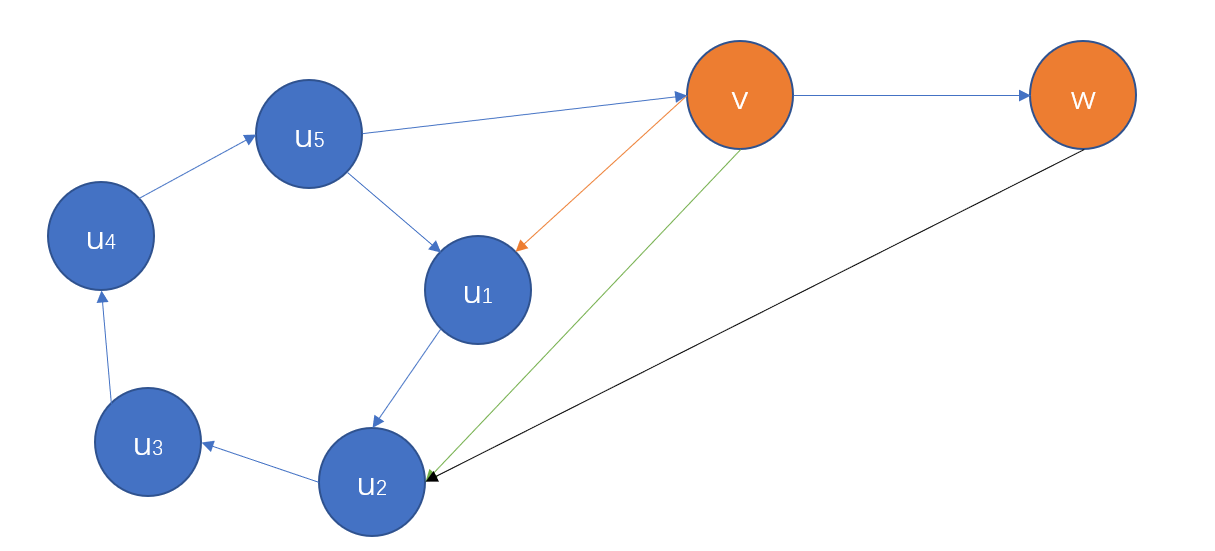
上图中,蓝线可以认为是原哈密顿路径中的边,橙线是直接连首,绿线是找到第一个 \(x\) 满足 \(v\) 指向 \(u_x\) ,黑线是路径 \(v\to w\to u_2\to u_3\to u_4\to u_5\to u_1\to v\)
ok, 现在我们知道了竞赛图有这样的性质,那么我们不妨先对原图使用 tarjan 缩成一个个强联通分量,对于每个强联通分量内,点可以互通,并且存在哈密顿回路
因为存在回路,而且这个强联通分量里的每个点都存在指向下一个强联通分量的边(否则可以合并成新强连通,注意这是一张完全图)。
所以从任意一个点进入一个强连通分量都可以遍历全部点,并从此强连通分量指向的下一个强连通分量遍历。
考虑 DP 计算出从这个点出发所能找到的最长的路径长度
然后 \(dfs\) 输出路径,本题难点在于构造出每个强连通分量的哈密顿回路,有亿点点代码细节....
可以发现缩点是 \(O(n)\) 的,而哈密顿回路的构造是 \(O(n^2)\) ,\(dp\) \(O(n)\) ,所以总共也就是 \(O(n^2)\)
Code
代码参考了 POI2017]Turysta - NeighThorn - 博客园 (cnblogs.com) ,这里我的压行可能不是很常规
对于 \(find()\) 找哈密顿回路的部分,有这样一个图可能好理解一点:
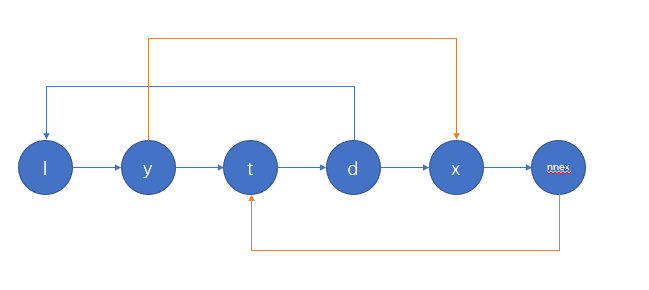
蓝线是原回路(\(l\to y\to t\to d\to l\)),新回路:\(t\to d\to l\to y\to x\to nnex\to t\)
注意下面代码在 \(while\) 最开始的时候虽然我们知道有回路 \(l\to \dots \to d\to l\) ,但 \(nex[d]\neq l\)
#include<bits/stdc++.h>
using namespace std;
const int N = 2e3+5;
int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
bool chkmax(int &a,int b){return a<b?a=b,1:0;}
int edge[N][N],Edge[N][N],dfn[N],low[N],scc[N],siz[N];
int stk[N],nex[N],nt[N],rt[N],q[N],f[N];
int n,top,tim,cnt,tail;
bool instk[N],vis[N],can[N];
void mark(int u){
vis[u]=true;
for(int i=1;i<=tail;++i)
if(edge[q[i]][u])can[q[i]]=true;// q[i] 可以到达一个环上的点
}
void find(){
int l=q[1],r=q[1];
for(int i=2,x;x=q[i],i<=tail;++i)//找哈密顿路径
if(edge[x][l])nex[x]=l,l=x;//指向首
else for(int now=l,last=0;;last=now,now=nex[now])
if(last==r){nex[r]=x,r=x;break;}//被尾指向
else if(edge[x][now]){nex[last]=x,nex[x]=now;break;}//插入中间
int d=l; mark(l);
while(d!=r){//在路径的基础上找回路,已经创建了一个回路 l->...->d
int x=nex[d];//想要扩展 x 点
if(edge[x][l])d=x,mark(x);//指向首
else for(int now=l,last=0;;last=now,now=nex[now])
if(edge[x][now]){nex[d]=l,nex[last]=x,l=now,d=x,mark(x);break;}//自己画图\doge
else if(last==d){//见上图,此时,x 前左右点都指向 x
int nnex,t;
for(int i=1;i<=tail;++i)if(!vis[q[i]]&&can[q[i]]){nnex=q[i];break;}
for(int i=l;;i=nex[i])if(edge[nnex][i]||i==d){t=i;break;}//t 是第一个 nnex 指向的点,t 之前的点都指向 nnex
for(int i=nex[d];i^nnex;i=nex[i])mark(i); mark(nnex);//这一段路都加入了环
nex[d]=l,l=t,d=nnex;// l=t 优化了时间
for(int now=l;;now=nex[now])
if(nex[now]==t){nex[now]=x;break;} //更改 t 在原路径上前一个点(y)的指向
break;
}
}
nex[r]=l;
for(int i=1;i<=tail;++i)
vis[q[i]]=can[q[i]]=false;
}
void tarjan(int u){
dfn[u]=low[u]=++tim;
instk[stk[++top]=u]=true;
for(int i=1;i<=n;++i)if(i!=u&&edge[u][i])
if(!dfn[i])tarjan(i),low[u]=min(low[u],low[i]);
else if(instk[i])low[u]=min(low[u],dfn[i]);
if(low[u]==dfn[u]){
siz[scc[u]=++cnt]=1,instk[rt[cnt]=u]=tail=0;
while(stk[top]!=u)
siz[scc[stk[top]]=cnt]++,
instk[stk[top]]=false,
q[++tail]=stk[top--];
q[++tail]=stk[top--];
find();
}
}
int dp(int u){
if(f[u])return f[u];
for(int i=1;i<=cnt;++i)
if(i!=u&&Edge[u][i])
if(chkmax(f[u],dp(i)))nt[u]=i;//强连通分量 u 下一个走 i 强连通分量
f[u]+=siz[u];
return f[u];
}
void print(int x){
if(!x)return ; printf("%d ",x);
for(int i=nex[x];i!=x;i=nex[i])printf("%d ",i);
print(rt[nt[scc[x]]]);
}
signed main(){
n=read();
for(int j=2;j<=n;++j)
for(int i=1;i<j;++i)
edge[i][j]=read(),edge[j][i]=edge[i][j]^1;
for(int i=1;i<=n;++i)if(!dfn[i])tarjan(i);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
if(edge[i][j]&&scc[i]!=scc[j])
Edge[scc[i]][scc[j]]=1;
for(int i=1;i<=cnt;++i)if(!f[i])dp(i);
for(int i=1;i<=n;++i)
printf("%d ",f[scc[i]]),print(i),puts("");
return 0;
}

