XVIII Open Cup, GP of Khamovniki G. Piecewise Linearity 题解

Statement

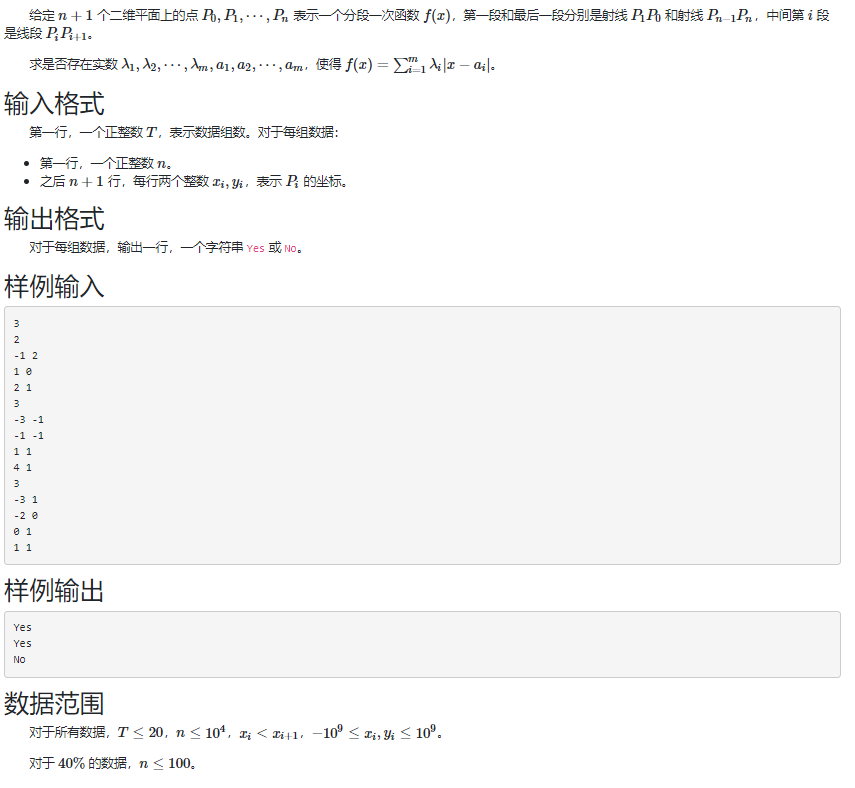
Solution

显然， \(f(x)\) 是一堆绝对值函数，which 最小值在 \(a_i\) 处取到，斜率为 \(k\) ，的累加

首先，我们可以利用计算器里面的画图看一看这种绝对值函数累加起来长什么样子

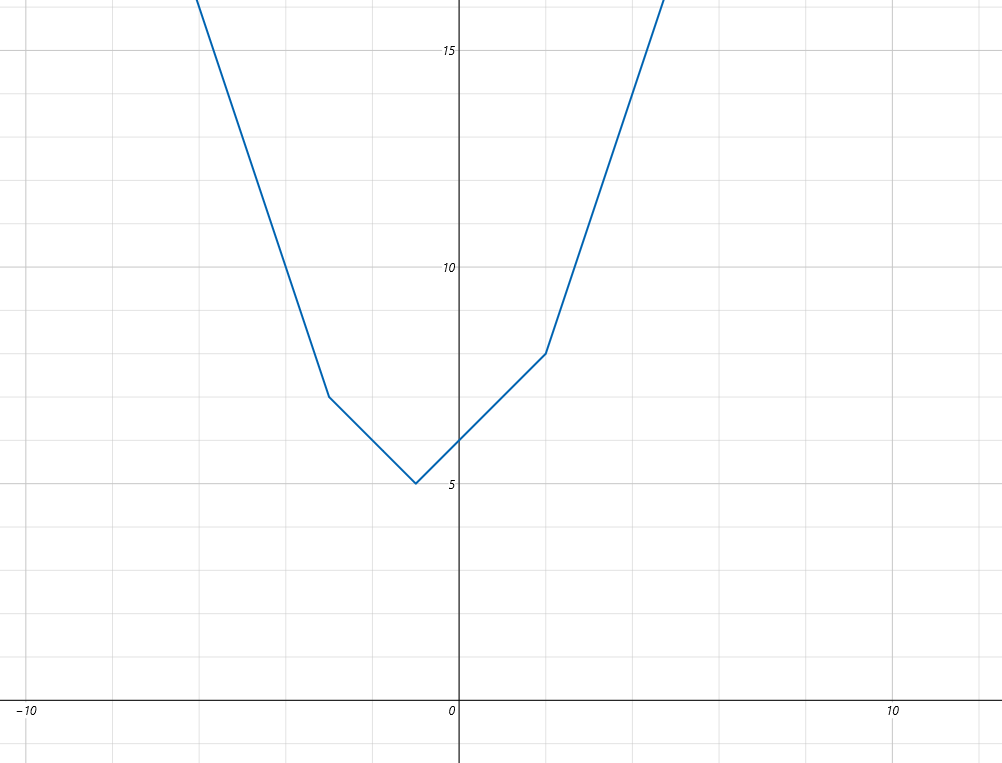
上面， \(f(x)=|𝑥+1|+|𝑥−2|+|𝑥+3|\)

发现拐点出现在 \(x=a_i\) 的位置，可以想到， \(a_i\) 只会有 \(n-1\) 个，且是 \(P_1\sim P_{n-1}\) 的横坐标。

显然，斜率是累加的，于是我们可以写出方程：

\[\begin{cases} k_1=-\lambda_1-\lambda_2-\cdots-\lambda_{n-1}\\ k_2=\lambda_1-\lambda_2-\cdots-\lambda_{n-1}\\ k_3=\lambda_1+\lambda_2-\cdots-\lambda_{n-1}\\ \cdots\\ k_n=\lambda_1+\lambda_2+\cdots+\lambda_{n-1}\\ \end{cases} \]

其中，\(k\) 已知，有 \(n-1\) 个未知数，\(n\) 个方程

所以我们没有必要采用高斯消元的方式来判断是否有解，只需要判断 \(k_1\) 是否等于 \(-k_n\) 即可（不考虑最后一个方程，可以得到一组解。加入最后一个方程，只需判是否矛盾）

或者，可以发现 \(k_{i+1}-k_i=2\times \lambda_i\) ，也可以直接解出来，带入第 \(n\) 个方程判断

---

现在，我们解决了斜率的问题，考虑截距

在知道了 \(\lambda_i\) 之后，我们可以考虑 \(O(n^2)\) 算每一个 \(b\) （截距），但是需要卡常

类似 \(k\) 的，我们可以写出 \(b\) 的式子；

\[b_x=-\sum_{i=1}^x \lambda _ia_i+\sum_{i=x+1}^{n-1}\lambda_ia_i \]

同样发现 \(b_{i+1}-b_i=-2\times\lambda_{i+1}a_{i+1}\) ，在求出 \(b_n\) 后，容易求出所有 \(b\)

然后与实际值判断一下即可，一共是 \(O(n)\) 的

另外一种思路是，观察到绝对值函数凑不出 \(|x-a|+c\) 的形式，所以假设没有常数，那么由定义式，

(这里的常数指的是 \(f(x)\) 的常数)

\[y_0=\sum_{i\in[1,n-1]}\lambda_i(x_i-x_0)=\sum_{i\in[1,n-1]}\frac{k_{i+1}-k_i}2(x_i-x_0)\\ y_n=\sum_{i\in[1,n-1]}\lambda_i(x_n-x_i)=\sum_{i\in[1,n-1]}\frac{k_{i+1}-k_i}2(x_n-x_i)\\ \therefore y_0+y_n=\sum_{i\in[1,n-1]}\frac{k_{i+1}-k_i}2(x_n-x_0)=\frac{k_n-k_1}2(x_n-x_0)\\ \]

这里，\(x_i,y_i\) 是 \(P_i\) 的横纵坐标。又知 \(k_1=-k_n\) ，所以

\[y_0+y_n=k_n(x_n-x_0)=\frac{y_n-y_{n-1}}{x_n-x_{n-1}}\times (x_n-x_0) \]

乘过去

\[(y_0+y_n)(x_n-x_{n-1})=(y_n-y_{n-1})(x_n-x_0) \]

容易发现，上面这个式子等价于常数为 \(0\) ,\(O(1)\) 判断

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5+5;;

void file(){
    freopen("math.in","r",stdin);
    freopen("math.out","w",stdout);
}
int read(){
    int s=0,w=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
    return s*w;
}

int x[N],y[N];
int T,n;

signed main(){
    //file();
    T=read();
    while(T--){
        n=read();
        for(int i=0;i<=n;++i)x[i]=read(),y[i]=read();
        if((y[n]-y[n-1])*(x[1]-x[0])+(y[1]-y[0])*(x[n]-x[n-1])
         ||(y[0]+y[n])*(x[1]-x[0])+(y[1]-y[0])*(x[n]-x[0]))puts("No");
        else puts("Yes");
    }
    return 0;
}