【BJOI2015】糖果 题解

Statement

BJOI2015 糖果 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Solve

10pts 暴力填写

50pts 首先可以注意到每一行的填写方案其实是独立的

也就是说，如果现在我知道了 用 \(\leq k\) 的数填写 \(m\) 个格子 符合单调不下降条件 的方案数，设为 \(s\)，那么最后

\[ans=A_{sum}^n \]

那么，考虑设 \(f[i][j]\) 表示填写前 \(i\) 个格子，第 \(i\) 个格子填写 \(j\) 的满足条件的方案数，则

\[f[i][j]=\sum_{k=1}^j f[i-1][k] \]

发现这是一个前缀和 ，设 \(sum[i][j] =\sum_{k=1}^j f[i][k]\) ，那么 \(f[i][j]=sum[i-1][j]\)

如果我们顺推的话，那么

\[sum[i][j]=sum[i][j-1]+sum[i-1][j] \]

我们可以滚掉一维，这样空间复杂度 \(O(n)\) ，时间复杂度 \(O(n^2)\)

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e3+10;

inline int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') { if(ch=='-') w*=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
	return s*w;  
}
int n,m,k,p,ans,temp=1;
int sum[N];

signed main(){
//	freopen("candy.in","r",stdin);
//	freopen("candy.out","w",stdout);
	n=read(),m=read(),k=read(),p=read();
	for(register int i=1;i<=k;i++) sum[i]=1;
	for(register int i=1;i<=m;i++)
		for(register int j=1;j<=k;j++) 
			sum[j]=(sum[j-1]+sum[j])%p;
	ans=sum[k];
	while(n--)temp=(temp*ans)%p,ans--;
	printf("%lld\n",temp);
	return 0;
}

100pts

求到 用 \(\leq k\) 的数填写 \(m\) 个格子 符合单调不下降条件 的方案数，设为 \(s\)，有两种方法

Way1

延续我们刚刚 \(dp\) 的思路，发现这个二维 \(sum\) 数组好像是固定的，我们尝试把他打出来：

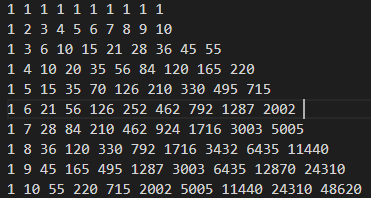
我们不妨把它转 \(45^{\text{o}}\) 看，发现这其实是一个杨辉三角的形式，我们知道杨辉三角其实对应组合数

我们最后要求的是什么呢，其实就是 \(sum[m][k]\)

不妨把杨辉三角也打出来看看：

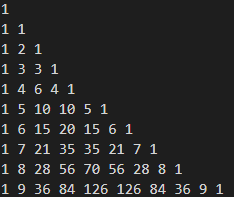
设 \(g[i][j]\) 表示杨辉三角第 \(i\) 行第 \(j\) 个数

Lemma \(sum[i][j]=g[i+j-1][j]\)

Proof 读者自证不难

于是我们有：

\[s=sum[m][k]=sum[k][m]=g[k+m-1][m]=C_{k+m-1}^{m} \]

Way2

注意到因为序列是单调不降的，所以我们只需要确定每个数在序列中出现了几次，就可以唯一确定这个序列。这个问题等价于下面这个问题：

有 \(m\) 个小球和 \(k\) 个盒子，小球全部相同而盒子互不相同，盒子可以为空，求将所有小球放入盒子的方案数。

在我们把球放入 \(k\) 个盒子的过程中，其实完成了一种排序，满足了单调不下降的条件。

考虑到求相同，用隔板法（把 \(m\) 个球分成 \(k\) 段，\(m-1\) 个空，\(k-1\) 个板，\(C_{m-1}^{k-1}\)）

考虑到盒子可以为空，不能直接用隔板法，那么不妨最开始就向每个盒子都放入一个小球，那么：

\[s=C_{m+k-1}^{k-1} \]

————————————

参考：题解 P5481 BJOI2015 糖果- Men always remember love because of romance only.

我们两种方法都得到了 \(s=C_{m+k-1}^{k-1}\) ,有:

\[C_{m+k-1}^{k-1}=\frac{(m+k-1)!}{(k-1)!m!}=\frac1{m!} \prod_{i=0}^{m-1}(k+i) \]

注意到 \(p\) 是任意模数，不符合逆元条件

我们可以选择分解出 \(m!\) 的质因数，算的时候干掉就可以了，注意到组合数是整数

直接分解的话复杂度大概是 \(O(m^2)\) ，（将 \(m\) 以内素数个数视作 \(m\) 级别），但其实还有优化的空间

Legendre’s formula 在正数 \(n!\) 的素因子标准分解式中，素数 \(p\) 的最高指数记作 \(L_p(n!)\) ，则 \(L_p(n!)=\sum_{k\ge 1}[\dfrac n{p^k}]\)

——百度百科

这样，分解复杂度就应该是 \(O(\sum_{prime[i]\leq m} \log_{prime[i]}m\approx \frac m{10})\)

或者，也可以直接扩展卢卡斯硬刚，但 \(P\) 有点大，（你忍一下

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5+5;

int read(){
	int s=0,w=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
	return s*w;
}

int n,m,k,p,cnt;
int prime[N],up[N],bas[N];
bool vis[N];

void getprime(int N){
	for(int i=2;i<=N;++i){
		if(!vis[i])prime[++cnt]=i;
		for(int j=1;j<=cnt&&prime[j]*i<=N;++j){
			vis[prime[j]*i]=1;
			if(i%prime[j]==0)break;
		}
	}
} 

signed main(){
	n=read(),m=read(),k=read(),p=read();
	if(!p)return puts("0"),0;
	getprime(m);
	for(int i=1;i<=m;++i)up[i]=m+k-i;
	for(int i=1;i<=cnt&&prime[i]<=m;++i)
		for(int j=prime[i];j<=m;j*=prime[i])
			bas[i]+=m/j;
	for(int i=1;i<=cnt;++i){
		int s=m+k-1-(m+k-1)%prime[i];
		for(int j=m+k-s;j<=m;j+=prime[i]){
			while(bas[i]&&up[j]%prime[i]==0)bas[i]--,up[j]/=prime[i];
			if(!bas[i])break;
		}
	}
	int s=1,ans=1;
	for(int i=1;i<=m;++i)s=s*up[i]%p;
	for(int i=1;i<=n;++i)ans=ans*(s-i+1)%p;
	printf("%lld\n",ans);
	return 0;
}

Extra

拓展一点东西，我们不妨在深究一下 Way1 中

\(sum[i][j]=g[i+j-1][j]\) 和 \(sum[i][j]=sum[i][j-1]+sum[i-1][j]\) 两个式子会产生什么东西：

\[sum[m+1][k]=\sum_{i=1}^k sum[m][i]=\sum_{i=1}^k g[m+i-1][i]=\sum_{i=1}^k C_{m+i-1}^i\\ sum[m+1][k]=g[m+k][k]=C_{m+k}^k \]

也就是说

\(C_{m+k}^k=\sum_{i=1}^k C_{m+i-1}^i\)