支配树学习笔记
Definition
给定 \(n\) 个点 \(m\) 条边的有向图 \(G=(V,E)\),其中 \(𝑉\) 是节点集,\(𝐸\) 是边集,且有 \(𝑉 = 𝑛, 𝐸 = 𝑚\)
规定 \(r \in 𝑉\) 为起点,且假设其能到达所有其他点
支配(dominate) 若对于两点 \(𝑥, 𝑦\) 满足任意以 \(r\) 为起点,\(𝑦\) 为终点的简单路径都经过 \(𝑥\),则称 \(𝑥\) 支配 \(𝑦\)
Nature
- 若 \(𝑥\) 支配 \(𝑦\),\(𝑦\) 支配 \(𝑧\),则 \(𝑥\) 支配 \(𝑧\),即支配关系满足传递性
- 若 \(𝑥\) 支配 \(𝑦\),\(𝑦\) 支配 \(𝑥\),则 \(𝑥 = 𝑦\)
- 若 \(𝑥, 𝑦, 𝑧\) 三个点互不相同,且 \(𝑥, 𝑦\) 均支配 \(𝑧\),则必有 \(𝑥\) 支配 \(𝑦\) 或 \(𝑦\) 支配 \(𝑥\)
上述三条,由支配定义,画图辅助即可证明,可以考虑反证法
Definition
直接支配点(immediate dominator)所有支配点中,离 \(𝑥\) 最近的点,称 \(𝑧\) 为 \(𝑥\) 的直接支配点(有时也称为最近支配点),记为 \(𝑧 = idom[x]\)
将 \((idom[x] , 𝑥)\) 连边,根据前面的支配性质,显然这样的边组成了一棵树,我们称其为支配树
不妨举个例子,此时,我们假设支配树的根节点、图的源点为 \(r=1\) ,那么,q我们可以得到支配树:
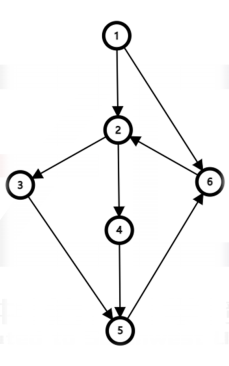
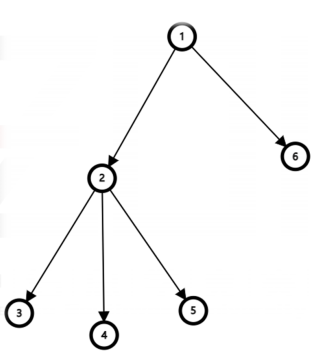
半支配点 (semi-dominator) 对于一个节点 \(y\),存在某个点 \(x\) 能够通过一系列点 \(𝑝_𝑖\)(不包含 \(x\) 和 \(y\))到达点 \(y\)且 \(∀𝑖, 𝑑𝑓𝑛[𝑖] > 𝑑𝑓𝑛[y]\),我们就称 \(x\) 是 \(y\) 的半支配点。 显然,半支配点并不唯一,但只保留 \(dfn\) 值最小的那个,记做 \(sdom[y] = dfn[x]\)
也就是说 \(\exist x\) ,可以通过 1 条/多条横叉边和一些树边从其他地方走过来
我们先对原图进行一次 \(dfs\) 并求出 \(dfn\)
(以下证明比较感性,由于是作者自己手推,所有可能会出现问题)
(突然发现后面好像将一个点的 \(dfn\) 值和它的编号混淆了,大家只要知道是指那个点就好)
Lemma
-
若 \(dfn[u]\leq dfn[v]\) ,则 \(\forall u\to v\) 的路径(不一定走 \(dfs\) 树边)上,必定经过 \(u,v\) 的一个公共祖先
Proof 考虑 \(u\to v\) 的路径:
- \(u\) 是 \(v\) 在 \(dfs\) 树上的祖先,此时显然成立
- \(u\) 不是 \(v\) 在树上的祖先,注意到此时 \(u\) 相对于 \(v\) 在更靠“左”的位置
- 经过前向边,设前向边 \((u,w)\) ,则问题转化成若 \(dfn[w]\leq dfn[v]\) ,则 \(\dots\)
- 经过返祖边,设返祖边 \((u,w)\) ,若 \(w\) 为二者公共祖先,问题结束,否则转化成 \(dfn[w]\leq dfn[v]\dots\)
- 经过横叉边,显然,横叉边的方向应该是从 \(dfn\) 值大的点到小的点,成立
简单来说, \(u\) 想要走出该子树,只能靠横叉边,而横叉边并不能向 "右" 跨越子树
所以,如果 \(u\) 可以到 \(v\) ,那么一定是靠返祖边跳出该子树,则一定经过公共祖先
-
\(idom[x]\) 是 \(x\) 在 \(dfs\) 树上的祖先
Proof 反证法,如果不是,那么显然存在一条从根到 \(x\) 的路径(直接走树边)不经过 \(idom[x]\) 和定义相悖
-
\(sdom[x]\) 是 \(x\) 在 \(dfs\) 树上的祖先
Proof 我们考虑 \(sdom\) 的求解过程
- 对于所有连向 \(x\) 的有向边 \((y,x)\) ,\(sdom[x]=\min_{(y,x)\in E}{dfn[y]}\)
- 对于连向 \(x\) 的有向边 \((y,x)\) ,找到 \(y\) 在树上一个祖先 \(z\) ,如果\(dfn[z]>dfn[x]\) ,\(sdom[x]=\min(sdom[x],sdom[z])\)
设 \(fa_x\) 为 \(x\) 在 \(dfs\) 树上的父亲,此时,\(dfn[x]\geq dfn[fa_x]\geq sdom[x]\),由 Lemma 1 , \(sdom[x]\) 到 \(x\) 一定经过它们的公共祖先 \(z\) ,显然 \(dfn[z]<dfn[x]\) ,为满足 \(sdom\) 的定义,取 \(sdom[x]=dfn[z]\) 最优
所以 \(sdom[x]\) 是 \(x\) 在 \(dfs\) 树上的祖先
这里实际上也给出了计算 \(sdom\) 的方法
我们可以这样理解求解方法:\(y\) 通过一条横叉边到了 \(x\) 的位置,所以 \(sdom[z]\) 也能满足条件地到达 \(x\)
我们也可以从 “传递” 的视角来理解这样的求解方法,考虑这样一个图,图中数字的含义是 \(dfn\) 值
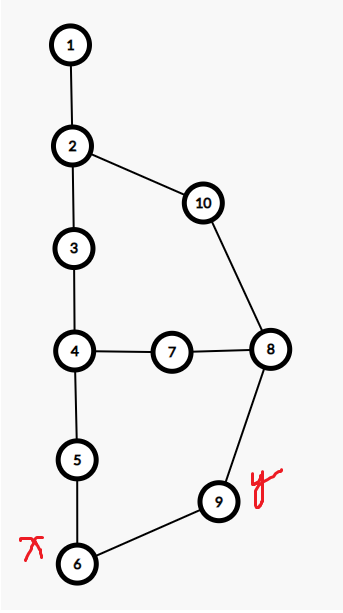
此时,假设我们在求解 \(sdom[x]\)
显然,我们可以用 \(5,9\) 来更新 \(sdom[x]\)
因为 \(dfn[y]>dfn[x]\) , \(y\) 在 \(dfs\) 树上的祖先 \(z\),如果 \(𝑑𝑓𝑛[𝑧] > 𝑑𝑓𝑛[𝑥]\), 那么 \(z\) 也将是 \(x\) 的半支配点,例如 \(z=8,7\)
更一般的:\(y\) 的半支配点 \(z\),如果满足 \(𝑑𝑓𝑛[𝑧] > 𝑑𝑓𝑛[𝑥]\)
那么 \(z\) 也将是 \(x\) 的半支配点 ,例如 \(10\)
-
\(idom[x]\) 为 \(sdom[x]\) 在 \(dfs\) 树上的祖先,或者就是 \(sdom[x]\)
Proof 这条引理揭示了 \(idom\) 和 \(sdom\) 的初步关系,反证法容易证明
-
删去所有非树边,连接 \((sdom[x],x)\) 后,原图的支配关系不变,且此时形成了一个 \(\text{DAG}\)
Proof 支配关系显然不变,可以通过 Lemma 4 感性理解,更好的感性理解可以去看 这个
通过这条引理,我们把一般图上的支配树求解转化成了 \(\text{DAG}\) 上的,相信大家都会在 \(\text{DAG}\) 上求支配树
虽然通过 Lemma 5 ,我们找到了一种 \(O(n\log n)\) 求解的方式(之后会说明 \(sdom\) 的求解是 \(O(n\ \alpha(n))\) 的)
但是,我们还有更高效的 \(\text{Lengauer Tarjan}\) 算法可以 \(O(n\ \alpha(n))\) 解决(不然搞这么多引理干嘛)
Theorem
设 \(y\) 为 \(sdom[x]\) 对应的点 到 \(x\) 的树边上 \(sdom\) 最小的点
- 若 \(sdom[x]==sdom[y]\) ,那么 \(idom[x]==sdom[x]\)
- 若 \(sdom[x]>sdom[y]\) ,那么 \(idom[x]==idom[y]\)
Proof
首先说明为什么不考虑小于的情况,
因为显然,设 \(sdom[x]\) 对应点 \(z\) ,\(z\) 包含 \(x\) 的子树的根为 \(y\)
此时 \(sdom[y]=dfn[z]\) ,相等,所以小于的情况是不存在的
重设 \(y\) 为 \(sdom[x]\) 对应的点 到 \(x\) 的树边上 \(sdom\) 最小的点
考虑第一部分
-
感性理解: \(sdom\) 可以理解成有一条路径从其他位置利用一条或多条横叉边走来
那么,阻碍 \(sdom[x]\) 成为 \(idom[x]\) 的地方在于可能存另一条路径可以从根到 \(x\) 而不经过 \(sdom[x]\)
那这样的路径应该是怎么样的呢?它应该是从某条横叉边直接进入到 \(sdom[x]\) 到 \(x\) 的一条树边上,然后再可以从树边到达 \(x\)
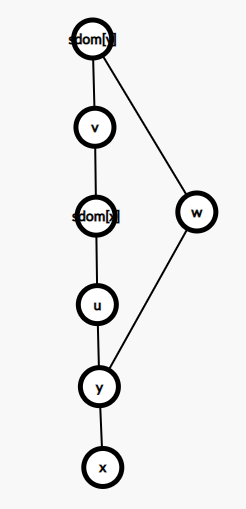
所以,如果 \(sdom[x]==sdom[y]\) ,那么意味着这个 \(y\) 就只能是上图中的节点 \(v\) ,此时不存在某一条路径可以偷渡,符合了 \(idom[x]\) 的定义
-
严格证明可以去看 Tarjan 的论文
考虑第二部分,就直接写感性理解了
也就是说,现在存在一条路径可以偷渡,考虑如何堵上这条可以偷渡的路径
自然,由于 \(y\) 是 \(sdom\) 最小的,我们取 \(idom[x]=idom[y]\) 即可
于是,此定理得证,我们得到了 \(idom\) 的求解方法
我们考虑如何计算求解 \(sdom,idom\)
(突然发现前面好像将一个点的 \(dfn\) 值和它的编号混淆了,大家只要知道是指那个点就好)
(首尾呼应/xyx)
考虑逆 \(dfn\) 序在反图上求解,将这个点与它 \(dfs\) 树上的父亲在带权并查集连边
而并查集带的权,就是并查集中这个点到根节点的路径上的所有点,\(sdom[x]\) 最小的 \(x\) 是哪个
找 \(sdom\) 直接找即可,找 \(idom\) 则在 \(sdom\) 处处理的信息即可
Code
代码参考了:题解 P5180 - hezlik 的博客
注意,这里为了写代码的方便,改 \(sdom[x]\) 的定义为
半支配点 (semi-dominator) 对于一个节点 \(y\),存在某个点 \(x\) 能够通过一系列点 \(𝑝_𝑖\)(不包含 \(x\) 和 \(y\))到达点 \(y\)且 \(∀𝑖, 𝑑𝑓𝑛[𝑖] > 𝑑𝑓𝑛[y]\),我们就称 \(x\) 是 \(y\) 的半支配点。 显然,半支配点并不唯一,但只保留 \(dfn\) 值最小的那个,记做 \(sdom[y] = x\)
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
const int M = 3e5+5;
vector<int>Edge[N][3];
//Edge[][0] 原图 1 反图 2 支配树
int f[N],fa[N],mn[N],sdom[N],idom[N],dfn[N],rev[N],ans[N];
int n,m,tim;
void dfs(int u){
rev[dfn[u]=++tim]=u;
for(auto v:Edge[u][0])
if(!dfn[v])dfs(v),fa[v]=u;
}
int find(int x){
if(f[x]==x)return x;
int res=find(f[x]);
if(dfn[sdom[mn[f[x]]]]<dfn[sdom[mn[x]]])mn[x]=mn[f[x]];
return f[x]=res;
}
void tarjan(){
for(int i=1;i<=n;++i)
f[i]=sdom[i]=mn[i]=i;
for(int i=tim;i>=2;--i){
int x=rev[i];
for(auto v:Edge[x][1]){//反图
if(!dfn[v])continue;//不连通
find(v);
if(dfn[sdom[mn[v]]]<dfn[sdom[x]])sdom[x]=sdom[mn[v]];
}
f[x]=fa[x],Edge[sdom[x]][2].push_back(x);
for(auto v:Edge[x=fa[x]][2]){
find(v);
if(sdom[mn[v]]==x)idom[v]=x;
else idom[v]=mn[v];//此时idom[v]可能没有找到
}
Edge[x][2].clear();
}
for(int i=2;i<=tim;++i){
int x=rev[i];
if(idom[x]^sdom[x])idom[x]=idom[idom[x]];
Edge[idom[x]][2].push_back(x);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1,u,v;i<=m;++i)
scanf("%d%d",&u,&v),
Edge[u][0].push_back(v),
Edge[v][1].push_back(u);
dfs(1);
tarjan();
for(int i=tim;i>=2;i--)
ans[idom[rev[i]]]+=++ans[rev[i]];
ans[1]++;
for(int i=1;i<=n;++i)
printf("%d ",ans[i]);
return 0;
}

