斜率优化DP入门

参考蓝书。

斜率优化的模型一般是：

f [i] = {min / max}_{L (i) \leq j \leq R (i)} f [j] + v a l (i, j)

$f[i]={\min/\max}_{L(i)\leq j\leq R(i)}{f[j]+val(i,j)}$

其中， $val(i,j)$ 仅和 $i$ 或 $j$ 有关时，我们可以想到单调队列优化

当其同时与 $i,j$ 有关，我们可以想到斜率优化

「TYVJ1098」任务安排 1

题面

$N$ 个任务排成一个序列在一台机器上等待完成（顺序不得改变），这 $N$ 个任务被分成若干批，每批包含相邻的若干任务。从时刻 $0$ 开始，这些任务被分批加工，第 $i$ 个任务单独完成所需的时间是 $T[i]$ 。在每批任务开始前，机器需要启动时间 $S$ ，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。每个任务的费用是它的完成时刻乘以一个费用系数 $C[i]$ 。请确定一个分组方案，使得总费用最小。例如： $S=1；T=\{1,3,4,2,1\}；C=\{3,2,3,3,4\}$ 如果分组方案是 $\{1,2\}、\{3\}、\{4,5\}$ ，则完成时间分别为 $\{5,5,10,14,14\}$ ，费用 $W=\{15,10,30,42,56\}$ ，总费用就是 $153$ 。

输入

第一行是 $N(1\leq N\leq 5000)$ 。第二行是 $S(0\leq S\leq 50)$ 。下面 $N$ 行每行有一对数，分别为 $T[i]$ 和 $C[i]$ ，均为不大于 $100$ 的正整数，表示第 $i$ 个任务单独完成所需的时间是 $T[i]$ 及其费用系数 $C[i]$ 。

输出

一个数，最小的总费用。

样例

样例输入1

样例输出1

解题

考虑 DP

我们首先设状态： $f[i][j]$ 表示前 $i$ 个任务分成 $j$ 批执行的最先费用

那么有状态转移方程：

$f[i][j]=\min_{j-1\leq k<i}\{f[k][j-1]+val(k,i)\}$

其中， $val(k,i)=(S*j+sumT[i])\times(sumC[i]-sumC[j])$

其中， $sumT[i]=\sum_{j=1}^i T[j],sumC[i]=\sum_{j=1}^i C[j]$

即，考虑第 $j$ 批任务执行的是 $k+1\dots i$ 个任务

但这样是 $O(n^3)$ ,爆了，我们需优化。

注意到题目并没有规定分成多少批次

之所以需要批次，是因为想知道有多少次启动时间S，从而计算出每批任务完成的时间

实际上，可以将每批任务花费的启动时间S，对之后任务的影响提前计算

$----------$

状态： $f[i]$ ，表示前 $i$ 个任务划分成若干批执行的最小费用。

考虑当前批次执行的任务，有状态转移方程：

f [i] = min_{0 \leq j < i} {f [j] + s u m T [i] * (s u m C [i] - s u m C [j]) + S * (s u m C [n] - s u m C [j])}

$f[i]=\min_{0\leq j<i}\{f[j]+sumT[i]*(sumC[i]-sumC[j])+S*(sumC[n]-sumC[j])\}$

怎么理解呢？

当前批次执行的任务为第 $j+1\dots i$ 个任务

第一部分是直接把 $sumT[i]$ 当做这批的结束时间（之前的启动时间已经在 $f[j]$ 中）

第二部分，机器的启动时间会对第 $j$ 个任务以后的所有任务产生影响，提前将影响累加到最小费用中

时间复杂度 $O(n^2)$

这其实是 **费用提前计算 **的经典思想

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e3+5;

int n,s,t[N],c[N],f[N];

signed main(){
	scanf("%lld%lld",&n,&s);
	for(int i=1;i<=n;++i)
		scanf("%lld%lld",&t[i],&c[i]),
		t[i]+=t[i-1],c[i]+=c[i-1];
	memset(f,127,sizeof(f));
	f[0]=0;
	for(int i=1;i<=n;++i)
		for(int j=0;j<i;++j)
			f[i]=min(f[i],f[j]+t[i]*(c[i]-c[j])+s*(c[n]-c[j]));
	printf("%lld\n",f[n]);
	return 0;
}

「POJ1180」任务安排 2

题面

同任务安排 1

数据范围： $1\leq n\leq3e5,1\leq s,T[i],C[i]\leq512$

解题

芜湖， $O(n^2)$ 过不了了

我们考虑对状态转移方程进行变形

\begin{aligned} (1) & f [j] & = f [i] + s u m T [i] * (s u m C [j] - s u m C [i]) + S (s u m C [j] - s u m C [n]) \\ (2) & = (s u m T [i] + S) s u m C [j] + f [i] - s u m T [i] s u m C [i] - S * s u m C [i] \end{aligned}

$\begin{align} f[j]&=f[i]+sumT[i]*(sumC[j]-sumC[i])+S(sumC[j]-sumC[n])\\ &=(sumT[i]+S)sumC[j]+f[i]-sumT[i]sumC[i]-S*sumC[i] \end{align}$

可以把去掉 $\min$ 想成，直接把 $j$ 当做 $i$ 的决策点

上面最后得到的是以 $j$ 为主元的式子，这启发我们：

将每个决策点 $j$ ，视为二维平面上的点。

将 $sumC[j]$ 看作是横坐标， $f[j]$ 看作是纵坐标，那么上式就是一个形如 $y=kx+b$ 的一条直线

$k=sumT[i]+S,b=f[i]-sumT[i]sumC[i]-S*sumC[i]$

我们的目的是让 $f[i]$ 有尽量小的取值，

也就是让 $b$ 有尽量小的取值，因为 $b$ 中，除了 $f[i]$ 都是定值

也就是挑选一个合适的 $sumC[j]$ ，使得 $y-kx$ 尽量小

也就是将直线 $y^{\prime}=(sumT[i]+S)x$ 从坐标轴的最下方往上移，碰到的第一个点就是最优决策点，因为此时的平移距离 $b$ 最小。

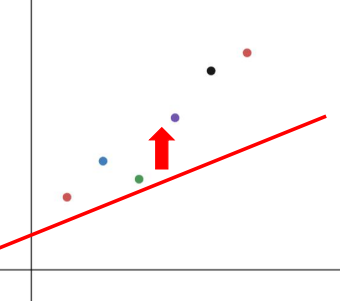
这就是“斜率”的含义了，那么“优化”呢？

回顾我们DP优化的关键：及时排除无用决策

可以想到，一些决策点 $(sumC[j],f[j])$ 是无用的。

假设存在三个决策 $j_1$ ， $j_2$ ， $j_3$ ，对应的决策点为 $(sumC[j_1],f[j_1 ])，(sumC[j_2 ],f[j_2 ])， (sumC[j_3 ],f[j_3 ])$ ，设三点分别为 $A，B，C$ 。

设 $j_1<j_2<j_3$ , $\because T,C\in \Z\therefore sumC[j_1]<sumC[j_2]<sumC[j_3]$

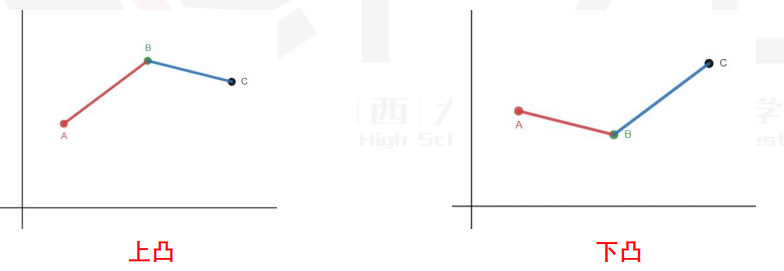
由图可知，在上凸情况下， $B$ 点是无用的，下凸情况下，如果：

\frac{f [j_{2}] - f [j_{1}]}{s u m C [j_{2}] - s u m C [j_{1}]} < \frac{f [j_{3}] - f [j_{2}]}{s u m C [j_{3}] - s u m C [j_{2}]}

$\frac{f[j_2]-f[j_1]}{sumC[j_2]-sumC[j_1]}<\frac{f[j_3]-f[j_2]}{sumC[j_3]-sumC[j_2]}$

$B$ 才是有用的。

我们按照上述的规则，排除掉所有无用决策点，将剩下的点集相邻两点连线

形成的线段的斜率从左到右是单调递增，实际上需要维护的是一个下凸壳

我们可以使用单调队列

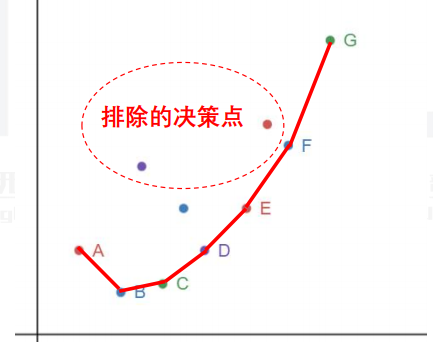
哪一个点是最优决策呢？

对于斜率为 $k$ 的直线，若某个点左侧线段的斜率小于 $k$ ，右侧线段的斜率大于 $k$ ，那么该点就是最优决策点

如何在斜率单调递增的队列中找到最优决策点？

二分，那么时间复杂度为 $O(n\log n)$ ，已经足够过掉这道题了。

但，还能不能再优化？

我们观察刚刚的式子：

f [j] = (s u m T [i] + S) s u m C [j] + f [i] - s u m T [i] s u m C [i] - S * s u m C [i]

$f[j]=(sumT[i]+S)sumC[j]+f[i]-sumT[i]sumC[i]-S*sumC[i]$

$sumC$ 是单调递增的，新的决策点的横坐标一定大于之前所有决策点的横坐标
斜率 $S+sumT[i]$ 单调递增的

由上述两点，我们只需要维护相邻两点线段斜率大于 $S+sumT[i]$ 的决策点，那么最优决策点就是队头

具体的，对于每个状态 $i$ :

检查队头的两个决策 $q[l]$ 和 $q[l+1]$ ，若斜率 $\dfrac{f[q[l+1]]-f[q[l]]}{sumC[q[l+1]]-sumC[q[l]]}\leq S+sumT[i]$ 则将 $q[l]$ 出队，继续检查队头
直接取出队头 $q[l]$ 为最优决策，计算 $f[i]$ 。
将新决策 $i$ 加入队尾，插入前，若三个决策点 $j1=q[r-1]，j2=q[r]，j3=i$ 不满足下凸，则 $j2=q[r]$ 是无用决策，将 $q[r]$ 出队，继续检查队尾。

这就是优化了

• 维护队列中相邻两个元素的某种“比值”的“单调性”

• 因为该比值对应坐标系中的斜率

• 所以称为斜率优化

• 英文称为 $\text{convex hull trick}$ (直译：凸壳优化策略)

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 30005;

int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=10*x+ch-'0',ch=getchar();
	return x*f;
}

int n,s;
int q[N],t[N],c[N];
ll st[N],sc[N],f[N];

double calc(int i,int j){
	return double(f[j]-f[i])/(sc[j]-sc[i]);
}

int main() {
	memset(f,0x3f,sizeof(f));
	n=read();s=read();
	for(int i=1;i<=n;++i){
		t[i]=read();c[i]=read();
		st[i]=st[i-1]+t[i];
		sc[i]=sc[i-1]+c[i];
	}
	int l=1,r=0;
	q[++r]=f[0]=0;
	for(int i=1;i<=n;++i){
		while(l<r&&calc(q[l],q[l+1])<=s+st[i])l++;
		f[i]=f[q[l]]-(s+st[i])*sc[q[l]]+st[i]*sc[i]+s*sc[n];
		while(l<r&&calc(q[r-1],q[r])>calc(q[r],i))r--;
		q[++r]=i;
	}
	printf("%d",f[n]);
	return 0;
}

「BZOJ2726」任务安排 3

题面

同任务安排 1

数据范围： $1\leq n\leq3e5,1\leq s,C[i]\leq512,-512\leq T[i]\leq 512$

解题

芜湖， $T[i]$ 可以为负数，那么斜率 $S+sumT[i]$ 不在递增了

不能仅仅只维护相邻两点线段斜率大于 $S+sumT[i]$ 的决策点，需要维护所有下凸壳的决策点

如何找到最优决策？单调队列中二分

时间复杂度为 $O(n\log n)$

代码

#include <cstdio>
typedef long long ll; int n,s,q[300001];
ll f[300001],st[300001],sc[300001];
ll in(){
    ll ans=0; int f=1; char c=getchar();
    while ((c<48||c>57)&&c!='-') c=getchar();
    if (c=='-') c=getchar(),f=-f;
    while (c>47&&c<58) ans=ans*10+c-48,c=getchar();
    return ans*f;
}
int bs(int i,int k,int l,int r){
	if (l==r) return q[l];
	while (l<r){
		int mid=(l+r)>>1;
		if (f[q[mid+1]]-f[q[mid]]<=k*(sc[q[mid+1]]-sc[q[mid]])) l=mid+1;
		else r=mid;
	}
	return q[l];
}
int main(){
    n=in(); s=in(); q[1]=0;
    for (int i=1;i<=n;i++)
        st[i]=st[i-1]+in(),sc[i]=sc[i-1]+in();//费用提前计算
    f[0]=0; int l=1,r=1;
    for (int i=1;i<=n;i++){
    	int ans=bs(i,s+st[i],l,r);//二分求答案
        f[i]=f[ans]-(s+st[i])*sc[ans]+st[i]*sc[i]+s*sc[n];//动态规划
        while (l<r&&(f[q[r]]-f[q[r-1]])*(sc[i]-sc[q[r]])>=(f[i]-f[q[r]])*(sc[q[r]]-sc[q[r-1]])) r--;//队尾不满足单调递增
        q[++r]=i; 
    }
    return !printf("%lld",f[n]);
}
————————————————
版权声明：代码为CSDN博主「ssl_xjq_逐风之刃」的原创，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/sugar_free_mint/article/details/81949236

注意，这里如果我们直接用之前的 $calc$ 函数算斜率的话会被卡精度，需要用乘法。

任务安排4

$T[i]$ 为正数， $C[i]$ 可以为负数。

回顾那个式子：

f [j] = (s u m T [i] + S) s u m C [j] + f [i] - s u m T [i] s u m C [i] - S * s u m C [i]

$f[j]=(sumT[i]+S)sumC[j]+f[i]-sumT[i]sumC[i]-S*sumC[i]$

方法一

新增加的决策点的横坐标 $sumC[i]$ 不再单调递增，会插入到凸壳中间的位置，队列不能实现插入操作

什么东西支持插入、维护递增？

平衡树！

我们可以利用平衡树维护斜率单调性

方法二：

可以倒序DP，设计一个状态转移方程，让 $sumT$ 为横坐标， $sumC$ 为斜率的一项，转为为任务安排3 的情况，使用单调队列维护凸壳，使用二分查找求出最优策略

任务安排5

$T[i],C[i]$ 均可以为负数。

康康这位神犇的啦『任务安排斜率优化及其变形』 - Parsnip - 博客园

posted @ 2021-08-07 22:39 _Famiglistimo 阅读(104) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】

公告

昵称： _Famiglistimo
园龄： 4年3个月
粉丝： 29
关注： 22

+加关注

2025年3月

日

一

二

三

四

五

六

lost_heart_hurts

斜率优化DP入门

斜率优化DP入门

「TYVJ1098」任务安排 1

题面

输入

输出

样例

样例输入1

样例输出1

解题

代码

「POJ1180」任务安排 2

题面

解题

代码

「BZOJ2726」任务安排 3

题面

解题

代码

任务安排4

方法一

方法二：

任务安排5

公告

搜索

积分与排名

随笔分类

阅读排行榜

评论排行榜

推荐排行榜

最新评论