后缀数组学习笔记

后缀数组学习笔记

蒟蒻作者通过 ~(o°ω°o) (cnblogs.com) 和 后缀数组 - 百度文库 大致弄明了后缀数组

后缀数组本身是对字符串后缀进行排序的。

它有一个重要的前置知识，~~（蒟蒻作者最开始就死在这里 ~~ ，基数排序

它还可以解决许多关于字符串的问题，一个经典的应用是 LCP

我们从前置知识开始

基数排序

假设我们已经有了一点点基数排序的基础。

可以简单将基数排序的作用理解成对于一些 \(pair(p,q)\) 排序。

第一关键字 \(p\) 相等时，则比较第二关键字 \(q\)。

具体应用在这里，我们首先仅考虑将每个后缀第一个字符从小到大排序。

考虑把第 \(i\) 个字母看作 \((s[i],i)\) 这样的二元组。

这样我们可以保证 \(ascii\) 小的在前面，若 \(ascii\) 相同则先出现的在前面，然后

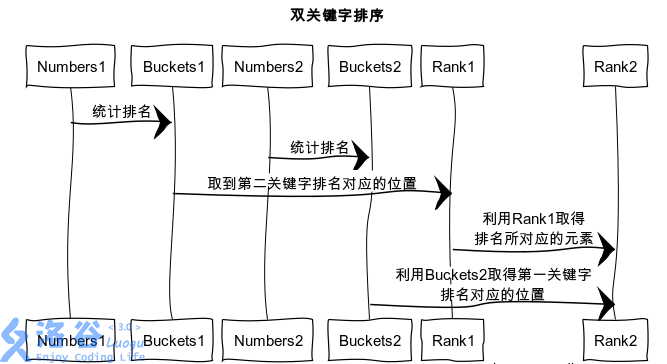
（图源：https://www.sohu.com/a/244143883_100201031)

（当然，蒟蒻作者并不是很看得懂这张图）

大体的意思是，将第一关键字放入一个桶 \(tax[i]\)，表示 \(i\) 出现次数

（这里实现了一个桶排序第一关键字对吧）

for(int i=1;i<=n;++i)tax[s[i]]++;

然后，我们做一个前缀和，统计排名（\(m\) 是值域范围）

for(int i=1;i<=m;++i)tax[i]+=tax[i-1];

现在，\(tax[i]\) 的意义变成了小于等于 \(i\) 的数的个数（联想排名的意义！！）

考虑到第二关键字的影响，对于第一关键字相同的情况（被分到同一个 \(tax\) ），我们应该按顺序分配排名

for(int i=n;i>=1;--i)rank[tax[s[i]]--]=i;

在这里 \(rank[i]\) 表示的意义是排名为 \(i\) 的下标位置。

（相信大家一定很容易意会这个倒序的意义所在）

其中 tax[i]-- 的目的是为了分配不同排名。

比如 \(('a',1),('a',2)\)，（大家一定还记得第二关键字的意义是下标）

有 \(tax['a']=2\)，我倒序枚举，第一次给 \(rank[2]\) 分配 \(2\)，第二次给 \(rank[1]\) 分配 \(1\)

（好像这并不是一个很好的例子）

意会意会，它的模板应该是这样的：

for(int i=1;i<=n;++i)

最后一个循环的重点是从大到小枚举第二关键字。

显然，时空复杂度 \(O(n)\)

后缀数组

我们现在进入正题。

暴力构造大概是 \(O(n^3)\) 的，显然不行。

比较高效的 \(\text{Multi-key Quick Sort}\) 也是 \(O(n^2)\)。

这些都太拉了，我不要，所以:

Definition：

首先，我们可以记 \(Suf(i)\) 表示字符串从 \(i\) 位置开始（到整个串末尾结束的一个）的后缀，也就是说 \(Suf(i)=s[i\dots strlen(s)]\)

后缀数组：\(sa[i]\) ，表示排名为 \(i\) 的后缀的起始位置。

名次数组：\(rk[i]\)，表示 $Suf(i) $ 的排名

（大家可能要仔细揣摩一下这个数组的含义）

也就是说，\(sa\) 保存 \(1\dots n\) 的某个排列 \(sa[1],sa[2]\dots sa[n]\) 使得 \(Suf(sa[i])\leq Suf(sa[i+1]),1\leq i< n\)

显然有 \(sa[rk[i]]=rk[sa[i]]=i\) ，这说明 \(sa\) 和 \(rk\) 是可以 \(O(n)\) 递推的。

求得这两个数组的方法大致有两种：

• \(O(n\log n)\) 的倍增
• $O(n) $ 的 \(DC3\)

由于蒟蒻作者不会第二种，并且，抛去理论时间复杂度，倍增法在常数、空间复杂度、代码复杂度完爆 \(DC3\) （这就是你懒得学的拙劣借口么

Solution:

我们记 \(Suf(i)_k\) 表示从 \(i\) 开始的后缀的前 \(k\) 个字符。

*我们可以把比较 \(s\) 的前 \(k\) 个字符叫做 \(k\) 意义下。

考虑倍增思想，我们已经知道了如何对每个后缀的第一个字符排序。

我们还可以发现一些显然的性质：

1. \(Suf(i)_{2k}=Suf(j)_{2k}\) \(\Leftrightarrow\) \(Suf(i)_k=Suf(j)_k,Suf(i+k)_k=Suf(j+k)_k\)
2. \(Suf(i)_{2k}<Suf(j)_{2k}\) \(\Leftrightarrow\) \(Suf(i)_k<Suf(j)_k或(Suf(i)_k=Suf(j)_k且Suf(i+k)_k<Suf(j+k)_k)\)

注意中间是等价符号。

观察第二个性质，在联想一下我们的双关键字排序是怎么做的，

我们发现，这其实可以理解成 对二元组 \((Suf(i)_k),Suf(i+k)_k)\) 排序后，就得到了 \(Suf(i)_{2k}\) 的顺序（即比较前 $ 2k$ 的字符意义下的 \(sa\) 数组）！！！

而我们还知道， \(sa\) 可以 \(O(n)\) 推求 \(rk\) 数组。

一个特殊情况是， \(i+k>n\) 怎么办？仔细想想，其实是没有影响的。

这么说，我们一共需要进行 \(\log n\) 次 \(O(n)\) 的过程，

可以在 \(O(n\log n)\) 的时间内计算出后缀数组 \(sa\) 和名次数组 $rk $

Code:

由于作者太菜了，我们直接通过代码讲解。

这里多了一个 \(tmp[i]\) 表示第二关键字中排名为 \(i\) 的后缀的位置

（具体在下面）

#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+5;

char s[N];
int n,m,rk[N],sa[N],tax[N],tmp[N];

void radix_sort(){//基数排序二元组 (rk[i],tmp[i])
    for(int i=1;i<=m;i++)tax[i]=0;
    for(int i=1;i<=n;i++)tax[rk[i]]++;
    for(int i=1;i<=m;i++)tax[i]+=tax[i-1];
    for(int i=n;i>=1;i--)sa[tax[rk[tmp[i]]]--]=tmp[i];
}

void suffix_sort(){
    m=75;
    for(int i=1;i<=n;i++)//后缀第一个字符
        rk[i]=s[i]-'a'+1,tmp[i]=i;
    radix_sort();
    for(int w=1,p=0;p<n;m=p,w<<=1){
        p=0;
        for(int i=1;i<=w;i++)tmp[++p]=n-w+i;//对第二关键字进行排序
        for(int i=1;i<=n;i++)if(sa[i]>w)tmp[++p]=sa[i]-w;
        radix_sort();
        swap(tmp,rk);
        rk[sa[1]]=p=1;//递推求 rk
        for(int i=2;i<=n;i++)
            rk[sa[i]]=(tmp[sa[i-1]]==tmp[sa[i]]&&tmp[sa[i-1]+w]==tmp[sa[i]+w])?p:++p;       
    }
    for(int i=1;i<=n;i++)
        printf("%d ",sa[i]-1);
}

int main(){
    scanf("%s",s+1);
    n=strlen(s+1);
    suffix_sort();
    return 0;
}

其中 \(m\) 是字符集大小，用于基数排序。（可以发现，字符集大小就是排名的个数）

由上面对基数排序的讲解，此时，第一个字母的相对关系我们已经知道了。

我们在这里用 $rk[i] $ 表示 \(Suf(i)_k\) ，\(tmp[i]\) 表示 \(Suf(i+k)_k\)

最开始，

for(int i=1;i<=n;i++)//后缀第一个字符
    rk[i]=s[i]-'a'+1,tmp[i]=i;
radix_sort();

我们得到了 \(Suf(i)_1\) 的大小关系。

注意这里必须是 s[i]-'a'+1 而不可以是 s[i] - 'a'，原因后面讲。

进行倍增：(\(w\) 是已知长度)

for(int w=1,p=0;p<n;m=p,w<<=1)

然后，我们根据 $w $ 意义下的 \(sa\) 数组（上一轮的结果），求得 $ 2w$ 意义下的 \(tmp\) ，即第二关键字中排名为 \(i\) 的后缀的位置。(这里的 \(p\) 仅仅是计数器)。我们其实可以把 \(tmp\) 看作是 \(sa\) 的 \(temp\)

for(int i=1;i<=w;i++)tmp[++p]=n-w+i;//对第二关键字进行排序
for(int i=1;i<=n;i++)if(sa[i]>w)tmp[++p]=sa[i]-w;

• 对于第一个 for：显然，有一些后缀是没有第二关键字的，即 \(Suf(i+w),i+w>n\)，

  我们需要把他们按顺序排在前面。

• 对于第二个 for：见图。

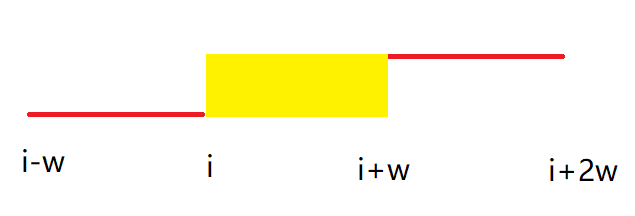
注意，我们的第二关键字指的是 \(Suf(i+w)_w\)，所以我们要减去一个 \(w\)

这时候，\(rk\) 已经有上一轮求好了，$tmp $ 的顺序也确定了，我们基数排序的最后一个循环的正确性得以保证，我们于是进行一个基数排序。

现在的唯一问题在于求新的，\(2w\) 意义下的 \(rk\)。

新的 \(rk\) 显然是会有重复的，因为我们在倍增的过程中只是对其前几个字符进行排名。

我们可以通过判掉一些重复的 \(rk\) 来优化一下 \(m\) ，即排名个数。

判断重复的方法很简单，其实就是我们之前所提到的性质一，所以我们有：

memcpy(tmp,rk,sizeof(rk));
rk[sa[1]]=p=1;//递推求 rk
for(int i=2;i<=n;i++)
    rk[sa[i]]=(tmp[sa[i-1]]==tmp[sa[i]]&&tmp[sa[i-1]+w]==tmp[sa[i]+w])?p:++p;   

这里，我们把 \(rk\) 在比较前 \(w\) 个字符意义下的值赋给 \(tmp\)

而下面的 \(rk\) 的意义表示的是在比较前 $2w $ 个字符意义下的

至此，后缀数组的基础部分大概就结束了。

讲一下刚刚说的 s[i]-'a'+1 的细节，在于这里在判定的时候，如果 \(sa[i]+w>n\)，\(tp = 0\)，如果 \(rk\) 本来就可以为 \(0\)，那么就导致不相同的被判定为相同。

典型的例子是 aaaaa，可以手算一下。

看看单用 \(sa\) 我们可以做什么？

（好像什么都不行

最长公共前缀

\(\text{(Longest Common Perfix)}\)

后缀数组是处理字符串的有力工具。

——罗穗骞

后缀数组一个重要的作用就是求出后缀之间的的最长公共前缀，它是发挥后缀数组作用的重要工具。

Definition:

\(lcp(s,t)=max\{i|s和t在i意义下相同\}\) ，也就是从头开始顺次比较 \(s[i]\) 和 \(t[i]\)。

\(LCP(i,j)=lcp(Suf(sa[i]),Suf(sa[j]))\) ,也就是排名 \(i\) 的后缀和排名位 \(j\) 的后缀的最长公共前缀。

我们先考虑如何求得 $LCP $

由定义，有性质：

• \(LCP(i,j)=LCP(j,i)\)
• \(LCP(i,i)=len(Suf(sa[i]))=n-sa[i]+1\)

这样，我们在计算 $LCP $ 的时候，就只需要考虑 \(i<j\) 的情况。

有这样一个引理：

Lemma: \(LCP(i,j)=\min(LCP(i,k),LCP(k,j))\) ，其中 \(1\leq i<k<j\leq n\)

设 \(p=\min(LCP(i,k),LCP(k,j))\)

我们可以先口胡一个简单证明：

Proof 1:

显然，\(s[sa[i]+LCP(i,k)+1]!=s[sa[k]+LCP(i,k)+1]\) ,\(s[sa[k]+LCP(j,k)+1]!=s[sa[j]+LCP(j,k)+1]\) ，而在之前的部分都是相同的，

也就是说：\(s[sa[i]\dots sa[i]+p]=s[sa[j]\dots sa[j]+p]\)

那么，\(LCP(i,j)\) 会不会大于 \(p\) 呢？反证法。

我们不妨假设 \(p=LCP(i,k)\), 即 \(LCP(i,k)<LCP(j,k),\)另外一个情况同理，

那么，至少有 \(s[sa[k]+p+1]=s[sa[j]+p+1]\)

若 \(p\) 增加 \(1\)（大于 \(LCP(i,k)\)），那么，\(s[sa[i]+p+1]=s[sa[j]+p+1]=s[sa[k]+p+1]\)

此时， \(LCP(i,k)=p+1\) ，矛盾。

所以，\(LCP(i,j)=\min(LCP(i,k),LCP(k,j))\)

Proof 2: 这个证明来自 后缀数组 - 百度文库 明显更为严谨。

（在文中，这条引理表述为：\(\forall 1\leq i<j<k\leq n,LCP(i,k)=\min(LCP(i,j),LCP(j,k))\)

我们设 \(p=\min(LCP(i,j),LCP(j,k))\)，那么有 \(LCP(i,j)\geq p,LCP(j,k)\geq p\)

设 \(Suf(sa[i])=u,Suf(sa[j])=v,Suf(sa[k])=w\)

由 \(u_{LCP(i,j)}=v_{LCP(i,j)}\) ，得 \(u_p=v_p\) ，同理有 \(v_p=w_p\)

所以 \(Suf(sa[i])_p=Suf(sa[k])_p\)

\[LCP(i,k)\geq p\qquad\qquad(1) \]

又设 \(LCP(i,k)=q>p\),则 \(u_q=w_q\)

而 \(\min{LCP(ij),LCP(j,k)}=p\) 说明 \(u[p+1]≠v[p+1]\) 或 \(v[p+1]≠w[q+1]\),

设 \(u[p+1]=x,v[p+1]=y,w[p+1]=z\)，显然有 \(x≤y≤z\)（后缀数组），又由 \(p<q\) 得 \(p+1≤q\),（所以u[p+1]=w[p+1]）

应该有 \(x=z\)，也就是 \(x=y=z\)，这与 $u[p+1 ]\neq v[p+1 ] $ 或 $v[p+1 ]≠w[q+1] $ 矛盾。所以：

\[LCP(i,k)\leq p\qquad\qquad(2) \]

由 \((1)(2)\) 式，\(LCP(i,k)=p=\min(LCP(i,j),LCP(j,k))\)

d饿到这个引理后，我们可以得到一个定理：

**Theorem: **设 \(i<j\) ，则 $ LCP(i,j)=\min{LCP(k-1,k)|i+1\leq k\leq j}$

我们已经知道了那个引理的正确性，这个定理的正确性是显然的，可以通过数学归纳法证明。

更进一步的，我们有：

Corollary: 对 \(i\leq j<k,LCP(j,k)\geq LCP(i,k)\)

\(---------\)

Definition:

\(height[i]=LCP(i,i-1)\) ,即排名为 \(i\) 的后缀和排名为 \(i-1\) 的后缀的最长公共前缀

\(H[i]=height[rk[i]]\) ，即 \(Suf(i)\) 和它前一名后缀的最长公共前缀

我们有：

Theorem: \(H[i]\ge H[i-1]-1\)

Proof:

定义 \(i=sa[rk[i]], j=sa[rk[i]-1], k=sa[rk[i-1]-1]\) (好像重复了，但是问题不大）

先对这张图有个印象：

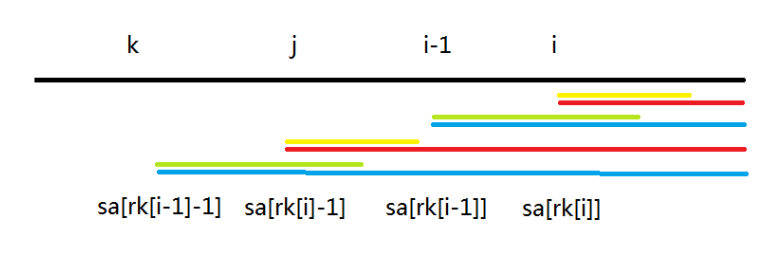
我们可以知道的是：

• \(Suf(i)>Suf(j)\)
• \(Suf(i-1)>Suf(k)\) ​
• \(H[i-1]=lcp(i-1，k)>1\) （注意这里 \(H[i - 1]\) 指的是需要证明的那个。若此条不成立，那么结论显然成立）

注意此处 lcp 和 LCP 的区别。

由此：

• \(lcp(k+1,i)=lcp(k,i-1)-1=H[i-1]-1\)​​​
• \(rk[k+1]\leq rk[i]-1\)

对于第一条： 想一想其实是显然对 ，我们同时在 \(Suf(k)\) 和 \(Suf(i-1)\) 前面减少一个相同字符（肯定相等），就得到了 \(LCP(k+1,i)\)

对于第二条：因为 \(Suf(i-1)>Suf(k)\),所以 \(Suf(i)>Suf(k+1)\)，那么，\(rk[i]>rk[k+1]\) ，那么 \(rk[k+1]\leq rk[i]-1\)

关注一下我们 \(i,j,k\) 的位置关系。在联想一下我们之前证明的 \(\text{Corollary}\) ,有：

\[\begin{align} LCP(rk[i]-1,rk[i])&\geq LCP(rk[k+1],rk[i])\\ &=lcp(k+1,i)\\ &=H[i-1]-1 \end{align} \]

这样的话，我们就可以在 \(O(n)\) 的时间中，递推求出 \(H\) 数组了。

大致的思想其实大家可能也猜得到，比较像 \(\text{KMP}\) 那种重复利用之前的信息

时间复杂度因为最多执行 \(O(n)\) 次 -1 ，指针最多移动 2n 次，所以就是 \(\mathcal{O}(n)\)

就直接放代码了：

void getheight() {
    int j,k=0;
    for(int i=1;i<=n;i++) {
        if(k)k--;
        int j=sa[rak[i]-1];
        while(s[i+k]==s[j+k])k++;
        height[rak[i]]=k;
    }
    for(int i=1;i<=n;i++)
        printf("%d ",height[i]);
}

应用

咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕

由于 wtcl ！

所以，咕咕。(这就你懒的拙劣借口？)

算了，给一道''例题'' P5353 树上后缀排序