整除分块详解
@ 前言
彩笔作者最开始以为是真分块。。。
作者接触到这玩意是因为这道题:luogu2261 [CQOI2007]余数求和
题目简洁明了,一看就是推式子的题:
给出正整数 \(n\) 和 \(k\),请计算
\(G(n, k) = \sum_{i = 1}^n k \bmod i\)
其中 \(k\bmod i\) 表示 \(k\) 除以 \(i\) 的余数。
$ 1\leq n,k\leq10^9$
首先暴力+小优化(\(n>k\) 的时候直接 \(ans+=(n-k)*k\)) 尝试了一波,可以,没想到居然水了 81 分 (正解吃**去吧)
然后开始推式子:
嗯。。然后@#¥%……&*。
然后就不知道了,于是看了一下题解发现了有个东西叫做整除分块
(话说我这样算不算同时写了一篇题解)
A 入门
终于进入正题了
由前言可以知道,整除分块是用来解决快速求这样 \(\sum_{i=1}^n\lfloor\frac{n}{i}\rfloor\) 的式子的一种方法
这个式子显然可以 \(O(n)\) 计算,也显然会T掉,所以我们需要加快
通过理性分析暴力打表可以发现这样一个特征:(下面是当 \(n=20\) 时候的情况)
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |16|17|18|19|20|
| ---------------------------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
| \(\lfloor\frac{20}{i}\rfloor\) | 20 | 10 | 6 | 5 | 4 | 3 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 |1|1|1|1|1|
(markdown好像炸了)
即: 表中同样的值会连续出现,成块状分布,所以从1到 \(n\) 的数组表可根据数值划分为不同的分块,且分块数远远小于 \(n\)
1.首先证明“分块数远远小于\(n\) ” ,也就是说,\(\lfloor\frac{n}{i}\rfloor\) 取值很少。
证:对于 \(i≤\sqrt n\) , 只有 \(\sqrt n\) 种,对于 \(i>\sqrt n\) ,\(\frac{n}{i}<\sqrt n\) ,也只有 \(\sqrt n\) 种取值,共计 \(2\sqrt n\) 种取值
现在还有一个问题是找到分块的点,如果我们可以 \(O(1)\) 找到,那么这个算法时间复杂度将会是优秀的 \(O(\sqrt n)\) :
2.设 \(\lfloor\frac n i\rfloor\) 与 \(\lfloor\frac {n}{i^{\prime}}\rfloor\) 相等,则 \(i^{\prime}\) 的最大值为 \(\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor\) 。
证:设 \(\lfloor\frac{n}{i}\rfloor=k\) ,有 \(ki+p=n,1\le p\le i\) ,
若 \(\lfloor\frac{n}{i+d}\rfloor=k\) ,有 \(k(i+d)+p^{\prime}=n\)
可以得到 \(p^{\prime}=p-kd\) ,所以当 \(p^{\prime}=0\) 时有 \(d_{max}=\lfloor\frac{p}{k}\rfloor\) ,于是:
原命题得证,此算法时间复杂度 \(O(\sqrt n)\)
当然还有更直接简明的证明方式:
有:
代码如下:
int ans=0;
for(int l=1,r;l<=n;l=r+1){
r=n/(n/l);
ans+=(r-l+1)*(n/l);
}
printf("%d\n",ans);
自动向下取整的啦
B 进阶
1.有时候,可能推出来的式子不一定就是一个很裸的整除分块,可能会与某些积性函数相乘,如:\(\phi\) 等这时候,我们就需要对这些函数统计一个前缀和。因为,每当我们使用整除分块跳过一个区间的时候,其所对应的函数值也跳过了一个区间。所以此时,就需要乘上那一个区间的函数值。
2.(公式太难打,就手写咯)
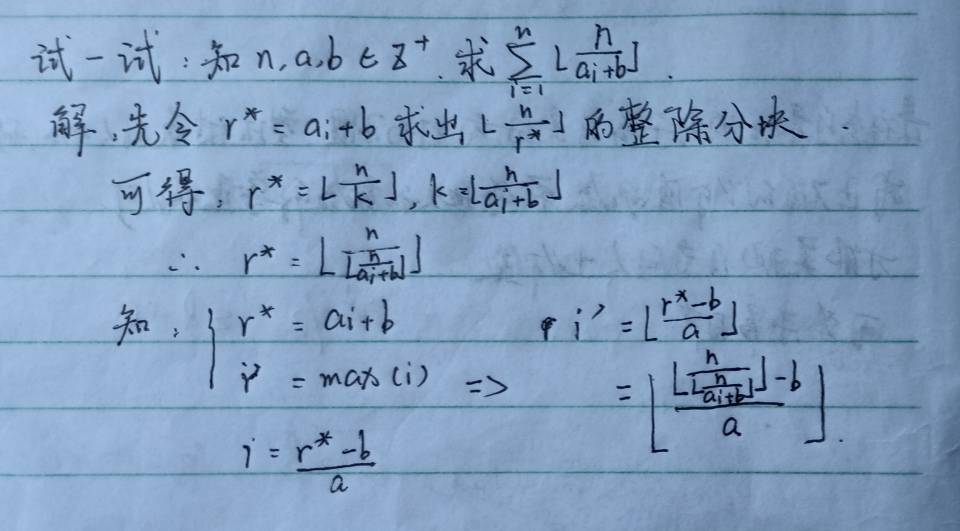
字丑勿喷,其实是换元法的应用
3.那向上取整呢?
我们知道:如果无法整除,那么 \(\lceil\frac ni\rceil=\lfloor\frac ni\rfloor+1\) ,而在整除时二者相等
所以我们不加1,我们加上 \(\frac{i-1}{i}\) 可以避免问题
所以最后得到的式子是:(呜呜呜,老老实实打公式)
\(i^{\prime}=\lfloor\frac{n-1}{k-1}\rfloor=\lfloor\frac{n-1}{\lfloor\frac{n+i-1}{i}\rfloor-1}\rfloor\)

