浅谈康拓展开
A 定义
一句话,给出一个全排列,求它是第几个全排列,叫做康托展开。
另一句话,给出全排列长度和它是第几个全排列,求这个全排列,叫做逆康托展开。
举例子理解:
| 排列组合 | 名次 | 康托展开 |
|---|---|---|
| 123 | 1 | 0 * 2! + 0 * 1! + 0 * 0! |
| 132 | 2 | 0 * 2! + 1 * 1! + 0 * 0! |
| 213 | 3 | 1 * 2! + 0 * 1! + 0 * 0! |
| 231 | 4 | 1 * 2! + 1 * 1! + 0 * 0! |
| 312 | 5 | 2 * 2! + 0 * 1! + 0 * 0! |
| 321 | 6 | 2 * 2! + 1 * 1! + 0 * 0! |
其实也就是按字典序增加编号递增,依次类推
B 康拓展开
先给出康托展开的公式:
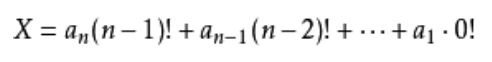
B1 理解1
对于一个序列 a, 序列的第 i 位(a[i])有 n+1-i 种选择,其中 n 是序列长度
变为进制数理解,这一位就是 n+1-i 进制的。
选择第 k 种选择,对应进制数的这一位就是 k
注意不能选择已经被选过的
选择完所有的位置,计算出每位进制数的值的总和,即为全排列数
举例:52341
- 首位5,五种选择{1,2,3,4,5}第5种,进制数为4
- 次位2,四种选择{1,2,3,4}第2种,进制数为1
- 中间位3,三种选择{1,3,4}第2种,进制数为1
- 次低位4,两种选择{1,4}第2种,进制数为1
- 末位1,一种选择{1}第1种,进制数为0
故生成的进制数为 41110
第 i 位的值就是 a[i] 减去它左边比它小的数的数量-1
//n表示全排列长度 for(int i=1;i<=n;i++) { cin>>a[i]; int x=a[i]; for(int j=1;j<=a[i];j++) x-=used[j]; //used[j]表示j是否用过(1用过,0没用) used[a[i]]=1; a[i]=x-1; }
有了变进制形式的结果,转换成10进制就可以了
long long res=0; for(int i=1;i<n;i++) res=(res+a[i])*(n-i);
B2 理解2
拿52413举例子:
1、首先看第一个数 5,不管第一位是什么数,后面都有四位数,那么这四位数全排列的方式有 4!种,而如果第一位是 1 或 2 或 3 或 4 都会比5开头的字典序要小,所以可以令1,2,3,4分别作为开头,这样的话就会有 4 * 4!种排法要比 52413这种排法的字典序要小。
那么第一个数是1,2,3,4时候的字典序的个数数完了是 4 * 4! 种,且这些字典序都要比52413的字典序要小。
还有其他的排列方式比52413的字典序要小的吗?
2、那么就可以固定第一位5,找下一位2,这时5已经用过了,所以从剩下的 1,2,3,4 里挑选比2小的数,一共1个,后面还剩三位,也就是3!种排列方式,那么这时候比 52413 字典序要小的又有 1 * 3!种,也就是当5在第一位,1在第二位的时候。
3、再看第三位4,这时5,2都用了,所以从剩下的 1,3,4三个数中找比4小的数的个数,有两个比4小原理同上,所以这时候也可以有 2 * 2!种排列方式的字典序小于 52413
4、再看第四位1,这时候会有 0 * 1!种
5、再看第五位3,这时候会有0 * 0!种
综上所述:
对于序列: 52413 该序列展开后为: 4 * 4! + 1 * 3! + 2 * 2! + 0 * 1! + 0 * 0! ,计算结果是: 106
由于是从0开始计数的,所以最后 52413 的编号为 107
//这里假设排列数小于10个
static const int FAC[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; // 阶乘 int cantor(int *a, int n) { int x = 0; for (int i = 0; i < n; ++i) { int smaller = 0; // 在当前位之后小于其的个数 for (int j = i + 1; j < n; ++j) { if (a[j] < a[i]) smaller++; } x += FAC[n - i - 1] * smaller; // 康托展开累加 } return x; // 康托展开值
}
tips: 这里主要为了讲解康托展开的思路,实现的算法复杂度为O(n^2),实际当n很大时,内层循环计算在当前位之后小于当前位的个数可以用 线段树来处理计算,而不用每次都遍历,这样复杂度可以降为O(nlogn)。
C 逆康拓展开
这里直接开栗子:
如果初始序列是12345(第一个),让你求第107个序列是什么。(按字典序递增)
这样计算:
先把107减1,因为康托展开里的初始序列编号为0
然后计算下后缀积:
1 2 3 4 5
5! 4! 3! 2!1! 0!
120 24 6 2 1 1
106 / 4! = 4 ······ 10 有4个比它小的所以因该是5 从(1,2,3,4,5)里选
10 / 3! = 1 ······ 4 有1个比它小的所以因该是2 从(1, 2, 3, 4)里选
4 / 2! = 2 ······ 0 有2个比它小的所以因该是4 从(1, 3, 4)里选
0 / 1! = 0 ······ 0 有0个比它小的所以因该是1 从(1,3)里选
0 / 0! = 0 ······ 0 有0个比它小的所以因该是3 从(3)里选
所以编号107的是 52413
(这里假设排列数小于10个)
static const int FAC[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; // 阶乘 //康托展开逆运算 void decantor(int x, int n) { vector<int> v; // 存放当前可选数 vector<int> a; // 所求排列组合 for(int i=1;i<=n;i++) v.push_back(i); for(int i=m;i>=1;i--) { int r = x % FAC[i-1]; int t = x / FAC[i-1]; x = r; sort(v.begin(),v.end());// 从小到大排序 a.push_back(v[t]); // 剩余数里第t+1个数为当前位 v.erase(v.begin()+t); // 移除选做当前位的数 }
D 线段树优化
D1 康托展开
我们看到,刚才的方法有两重循环,时间复杂度为O(N^2),找左侧用过的数的数量很费时间。
只要把左侧用过的数用线段树维护区间和,就可以只花log的时间就求出左侧小于自己的数的个数了。
//从这儿开始,tt是长度,n是线段树大小 for(int i=1;i<=tt;i++) { scanf("%d",&a[i]); upd(a[i]+n); //upd更新一个节点 a[i]-=sum(1,a[i],1,n,1)+1; //sum(x,y,l,r,root)=x到y的区间和,在l到r区间找,根节点在root }
这里所有数字都是单点修改,所以其实树状数组很香
线段树这种东西,就不展示了。
D2 逆康托展开
我们要完成的工作就是,对于每个数位a[i],求出x使得x前面的数中恰好有a[i]个0。
这里我们可以用二分,每次查询左子树上0的数量,如果不够,答案就在右子树,否则在左子树上继续找。
int fx(int l,int r,int x,int root) //在l到r范围找出有x个0的位置 { if(l==r)return l; int mid=(l+r)>>1,s=sum(l,mid,l,r,root); if(mid-l+1-s>x) return fx(l,mid,x,root<<1); return fx(mid+1,r,x-(mid-l+1-s),(root<<1)+1); } for(int i=1;i<=tt;i++) { int f=fx(1,n,a[i],1,0); upd(f+n); printf("%d ",f); }

