堆

堆 是一种特殊的树 ：

　　堆是一个完全二叉树:

　　堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。

堆必须是一个完全二叉树，除了最后一层，其他层的节点个数都是满的，最后一层的节点都靠左排列。

堆中的每个节点的值都必须大于(或小于等于)其子树中每个节点的值。

每个节点的值 都大于等于子树中每个节点值的堆叫"大顶堆"。

每个节点的值 都小于等于子树中每个节点值得堆叫“小顶堆”。

对于同一组数据可以构建多种不同形态的堆

 

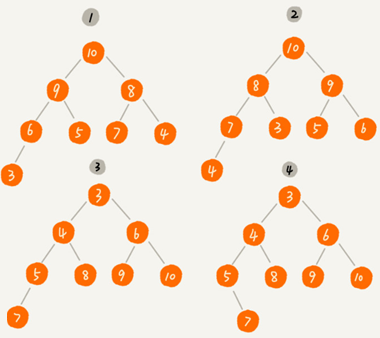
下图中1、2是大顶堆，3是小顶堆，4不是堆。

 

 

二、存储一个堆

完全二叉树比较适合用数组来存储。

用数组来存储完全二叉树，不需要存储左右子节点的指针，单纯地通过数组的下标，

就可以找到一个节点的左右子节点和父节点。

 

 

 

上图中i=1存储根节点，下标为 i 的节点的左子节点就是下标为 i∗2 的节点，

右子节点就是下标为i∗2+1的节点，父节点就是下标为 $\frac{i}{2}$ 的节点。

如果i=0存储根节点，下标为 i的节点的左子节点就是下标为 i∗2+1 的节点，

右子节点就是下标为 i∗2+2​的节点，但父节点的下标为(i-1)/2

 

堆的基本操作

1. 插入一个元素

往堆中插入一个元素后需要继续满足堆的两个特性。

把新插入的元素直接放到堆的最后，之前的堆就不再符合堆的特性。

就需要进行调整，让其重新满足堆的特性，这个过程叫作堆化（heapify）。

堆化有从下往上和从上往下两种方法。

 

 

堆化就是顺着节点所在的路径，向上或者向下进行对比，然后交换。

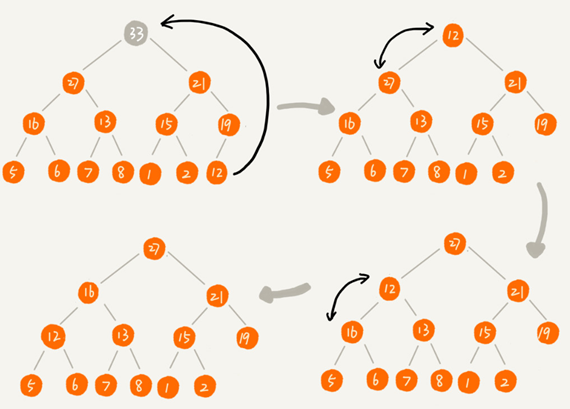
从下往上堆化是让新插入的节点与父节点对比大小。

如果不满足子节点小于等于父节点的大小关系，就互换两个节点。一直重复这个过程，直到比对到根节点。

 

 

2. 删除堆顶元素

堆的任何节点的值都大于等于（或小于等于）子树节点的值，

堆顶元素存储的就是堆中数据的最大值或者最小值。

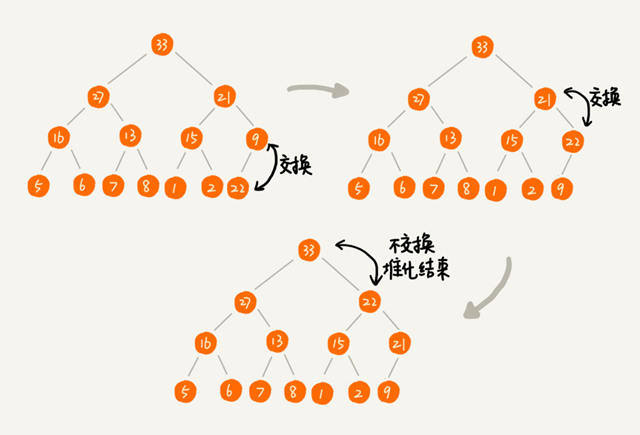
大顶堆的堆顶元素就是最大的元素，删除堆顶元素之后，就需要把第二大的元素放到堆顶，

那第二大元素肯定会出现在左右子节点中。

然后我们再迭代地删除第二大节点，以此类推，直到叶子节点被删除。

但这样操作完成后的堆不再满足完全二叉树的特性：

 

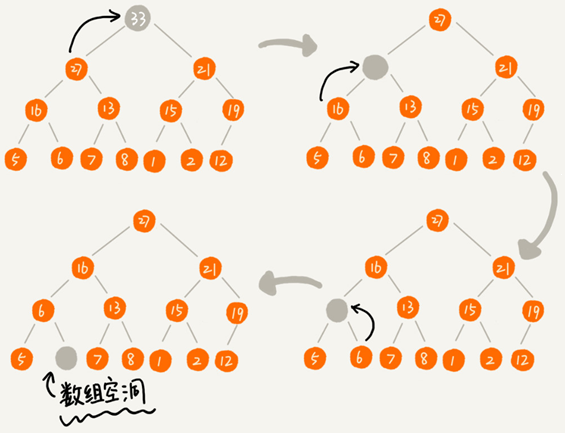
 可以先把最后一个节点放到堆顶，然后从上往下的堆化。

这种方法堆化之后的结果，肯定满足完全二叉树的特性：