快速排序

基本思想：

通过一趟排序将待排列记录分割成独立的两部分，其中的一部分均比另一部分小，然后分别对这两个部分进行排序，使整个序列有序。

可选择第一个记录pivotkey作为枢纽，设置两个指针low和high，初值分别为low和high。首先从high所指的位置向前搜索找到第一个比pivotkey小的值，并且移动到低端。然后从low所指位置向后搜索，找到第一个比pivotkey大的值，移动到高端。交替进行，直到low和high相遇。

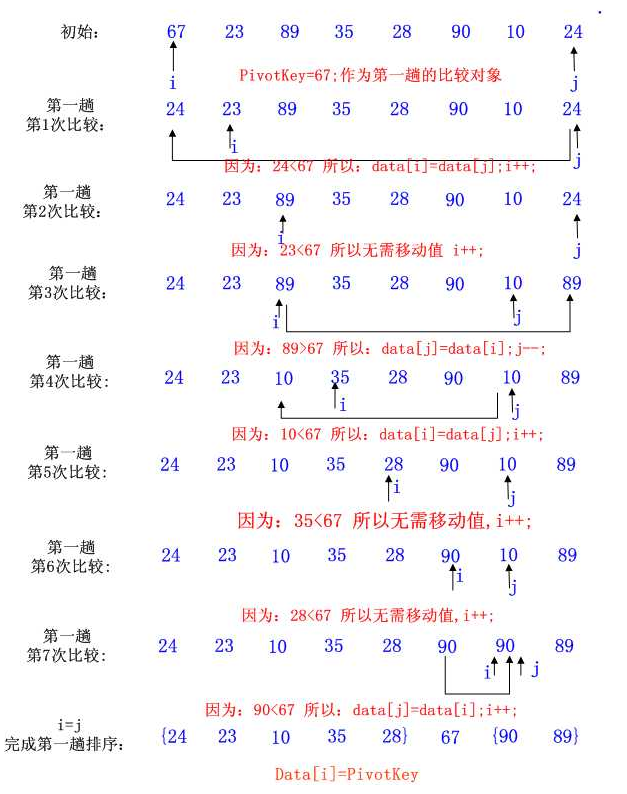
partition: j指向的是第一个比枢纽值小的值，也就是大数要放置的位置，找到第一个该位置的时候就该停止。同时由于该位置即将被放置一个大的数，所以需要把小的数放置到左边，以免被覆盖。

　　　　　i指向的是第一个比枢纽值大的值，所以要交换到右边j指向的位置。此时位置i也就是较小数放置的位置。所以将大数移动到右边之后，再从右边开始找到要移到左边的数。

              partition其实是找到一个大于枢纽值的数之后移到左边，找到一个小于枢纽值的数后移到右边，交替进行，直到2个指针相遇，就是枢纽值应该放的位置。

算法效率分析：

就平均速度而言，快速排序是已知内部排序方法中最好的一种排序方法,其时间复杂度为O(nlogn)；

在最坏情况下，快速排序所需的比较次数和冒泡排序的比较次数相同,时间复杂度为O(n2)；

快速排序需要一个栈作辅助空间，用来实现递归处理左、右子文件。在最坏情况下,递归深度为n，所需栈的空间大小为O(n)数量级。

快速排序是不稳定的。

算法实现代码：

//快速排序算法实现
//并且把原来的位置记录下来
#include<iostream>
using namespace std;
#include<vector>

int Partition(vector<int>& L,int low,int high,vector<int>& position)   
{
    int temp;
    L[0]=L[low];    //L[0]号位置是没有用的，用来存储枢纽值
    position[0]=position[low];    //position[0]存储的是枢纽值在L中的位置
    while(low<high)
    {
        while(low<high&&L[high]>=L[0]) --high;    //比哨兵位置大的值就不变，把high往前移
        L[low]=L[high];     //最初的时候，L[low]值已经存储到L[0]中去了。就释放了一个L[high]空位。
        position[low]=position[high];    //L[high]值交换到了低位，那么他在L中的位置也相应地移动到低位上
        while(low<high&&L[low]<=L[0]) ++low;     
        L[high]=L[low];
        position[high]=position[low];
    }
    //到此为止，low一定是等于high的
    L[low]=L[0];   //再把L[0]处的值还原到L[low]
    position[low]=position[0];   //把枢纽位置在L中的位置放到position应该有的位置中
    return low;
}

void QSort(vector<int>& L,int low,int high,vector<int>& position)
{
    if(low<high)
    {
        int pivotloc=Partition(L,low,high,position);
        QSort(L,low,pivotloc-1,position);
        QSort(L,pivotloc+1,high,position);
    }
}

void QuickSort(vector<int>& L,vector<int> &position)
{  
    for(int i=0;i<=L.size();i++)     //初始化位置矩阵
    {
        position.push_back(i);
    }
    QSort(L,1,L.size()-1,position);
}

void main()
{
    int L_t[10]={4,1,8,3,9,11,24,27,26,15};
    vector<int> L(L_t,L_t+10);     //用数组来初始化向量
    L.insert(L.begin(),0);      //把0号位空出来做哨岗
    vector<int> P;
    QuickSort(L,P);
    cout<<L[1]<<','<<L[2]<<','<<L[3]<<','<<L[4]<<','<<L[5]<<','<<L[6]<<','<<L[7]<<','<<L[8]<<','<<L[9]<<','<<L[10]<<endl;
    cout<<P[1]<<','<<P[2]<<','<<P[3]<<','<<P[4]<<','<<P[5]<<','<<P[6]<<','<<P[7]<<','<<P[8]<<','<<P[9]<<','<<P[10]<<endl;
}

 

面试题1：求长度为n的数组第k大的数：

算法思路：以第一个数作为参考数，进行一次partition。如果k比它所在的位置要大，那么就在该数的右边寻找，否则就在该数的左边寻找。直到找到排序为k的数为止。（算法复杂度为O（n））

代码如下：

int find_k(int *data,int n,int k)
{
    if(n<=0||k<=0||k>n)
        return -INT_MIN;
    int low=0;
    int high=n-1;
    return _find_k(data,low,high,k);
}

int _find_k(int *data,int &low,int &high,int k)
{
    int p=Partition(data,low,high);
    if(k-1==p)
        return data[p];
    else if(k-1>p)
    {
        low=p+1;
        _find_k(data,low,high,k);
    }    
    else if(k-1<p)
    {
        high=p-1;
        _find_k(data,low,high,k);
    }
}

int Partition(int *L,int low,int high)   
{
    int temp=L[low];       //哨兵位置
    while(low<high)
    {
        while(low<high&&L[high]>=temp) --high;    //比哨兵位置大的值就不变，把high往前移
        L[low]=L[high];     //最初的时候，L[low]值已经存储到L[0]中去了。就释放了一个L[high]空位。
        while(low<high&&L[low]<=temp) ++low;     
        L[high]=L[low];
    }
    //到此为止，low一定是等于high的
    L[low]=temp;   //再把L[0]处的值还原到L[low]
    return low;
}

 

面试题2：找到一个数组中出现次数超过一半的数。——剑指offer，面试题29

思路1：假设该数组已经排序了，那么出现次数超过一半的一定是排在该数组的中间。用find_k函数找到中位数，然后检测它是不是超过了一半，就可以得到结果。（算法复杂度为O（n））.

思路2：次数超过一半就是说该数出现的次数比其他所有的数的个数之和还要多。用一个值来存数数字，一个值来存储次数。当前数字出现时就在次数上加上1，出现其他的数就在次数上减去1，知道次数为0时，就将下一个数字保存下来。次数为0意味着目前为止，出现的不等于该数的个数已经跟它出现的个数相等了，所以所保存的值不再有优势。（算法复杂度为O（n））

int MoreThanHalf(int *data,int n)
{
    if(data==NULL||n<=0)
        return INT_MIN;
    int r=find_k(data,n,n/2+1);
    if(CheckMoreThanHalf(data,n,r))
        return r;
    else
        return INT_MIN;
}
bool CheckMoreThanHalf(int *data,int length,int number)
{
    bool isMoreThanHalf=false;
    int times=0;
    for(int i=0;i<length;i++)
    {
        if(data[i]==number)
            times++;
    }
    if(times>length/2)
        isMoreThanHalf=true;
    return isMoreThanHalf;
}

 面试题3：最小k个数  ——剑指offer，面试题30

思路1： 用快排的思想，找到第k大的数，并让比该数小的数放在它的左边。复杂度O(N)，会修改原数组。

思路2：堆排序的思想。设置一个大小为k的栈，按顺序放入k个数，并调整为最大堆。下一个数与堆顶进行比较，如果比堆顶小，则用该数取代堆顶的数，调整堆。复杂度O（nlogn），不会修改原数组。（适用于海量数据）