示例页面

python-因子分析FA

目录

1、起源

因子分析最早由英国心理学家C.Spearman发表了第一篇有关因子分析的文章《对智力测验得分进行统计分析》，从中提出的：他发现学生的英语、法语和古典语成绩非常有相关性，他认为这三门课程背后有一个共同的因素驱动，最后将这个因素定义为“语言能力”。由此解开了因子分析的序幕。

2、基本思想

因子分析通过研究众多变量间的内部依赖关系，探求观测数据中的基本结构，并用少数几个假想变量（因子）来表示基本的数据结构。原始变量是可观测的显在变量，而假想变量是不可观测的潜在变量，称为因子。

如在企业品牌形象研究中，消费者可通过24个指标构成的评价体系，对商场的方方面面进行优劣评价，但是消费者会主要关心3个放米娜，即商店的环境、商店的服务和商品的价格。因子分析可以通过24个变量，找出反应商店环境、商店服务水平和商品价格的3个潜在因子，对商店进行综合评价。

$ X{i} = u{_i} + a{_i}{_1}F{_1} + a{_i}{_2}F{_2} + a{_i}{_3}F{_3} + e{_i} $

$ F{_1} 、F{_2}、F{_3} $就是因子，不被包含的部分 \(e{_i}\) 叫特殊因子。

3、因子分析特点

  • 因子变量的数量 << 原有的指标变量数量。

  • 因子变量不是对原有变量的取舍，而是根据原有变量的信息进行重新组合，能够反映原有变量大部分的信息。

  • 因子变量不存在线性相关关系。

  • 因子变量具有命名解释性，即该变量是对某些原始变量信息的综合与反应。

4、算法用途

  • 降维，减少分析变量的数量

  • 分类，将内部具有关联变量/样本划分一类

5、分析步骤

  • a. 选择分析变量，并进行标准化处理

  • b. 计算变量间的相关系数矩阵、相关系数矩阵的特征值、特征向量

  • c. 充分性检验：KMO和巴特莱特球度检验，验证变量是否适合做因子分析。

KMO(Kaiser-Meyer-Olkin)检验

KMO检验统计量是用于比较变量间简单相关系数矩阵和偏相关系数的指标。数学定义为：

\[KMO{_i} = \frac{\sum\sum_{{_j}{_≠}{_i}} r^2 _{_i}{_j}}{\sum\sum_{{_j}{_≠}{_i}} r^2 _{_i}{_j} + \sum\sum_{{_j}{_≠}{_i}} p^2 _{_i}{_j}} \]

是否适合因子分析：KMO在0.9以上非常适合；0.8表示适合，0.7表示一般，0.6表示不太适合；0.5以下表示极不适合。

巴特莱特球度检验

该检验以原有变量的相关系数矩阵为出发点，其零假设\(H_0\)是：相关系数矩阵为单位矩阵，即相关系数矩阵主对角元素均为1，非主对角元素均为0（即原始变量之间无相关关系）。

依据检验统计量服从卡方分布，如果统计量卡方值较大且对应的sig值小于给定的显著性水平\(\alpha\)时，零假设不成立。即说明相关系数矩阵不太可能是单位矩阵，变量之间存在相关关系，适合做因子分析。

  • d. 提取公因子：只取方差>1或特征值>1（方差小于1的因子其贡献可能很小。）；因子的累积方差贡献率达到80%。

  • e. 因子旋转：提取因子的实际意义更容易解释

正交旋转和斜交旋转，其中主要使用正交旋转的方差最大旋转法。

  • f. 计算因子得分

6、应用实例

因子分析用到的库 factor_analyzer

pip install factor_analyzer

6.1 数据处理

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

# 导入数据
df = pd.read_csv(r'C:\Users\Desktop\bfi.csv')
df.head()


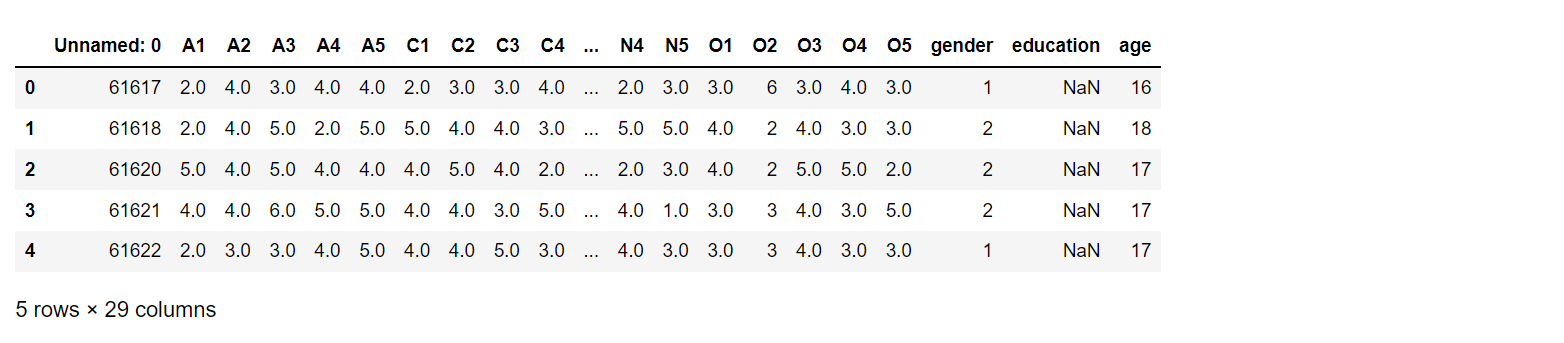
# 删除无关列
df.drop(["gender", "education", "age", "Unnamed: 0"], axis=1, inplace=True)

# 查看是否有缺失值
df.isnull().sum()

可以看到数据存在一些缺失值，需要对缺失值做删除处理

# 删除缺失值
df.dropna(inplace=True)
df.shape

处理完缺失值，样本数据大小为2436个样本 * 25个变量。

6.2 充分性检验

# 导入所需库
from factor_analyzer import FactorAnalyzer
from factor_analyzer.factor_analyzer import calculate_kmo
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity

# 因子分析可靠性检验

kmo_all, kmo_model = calculate_kmo(df)
chi_square_value, p_value = calculate_bartlett_sphericity(df)

print("kmo_all:", kmo_all, end="\n\n")
print("kmo_model:", kmo_model, end="\n\n")
print("chi_square_value:", chi_square_value, end="\n\n")
print("p_value:", p_value)

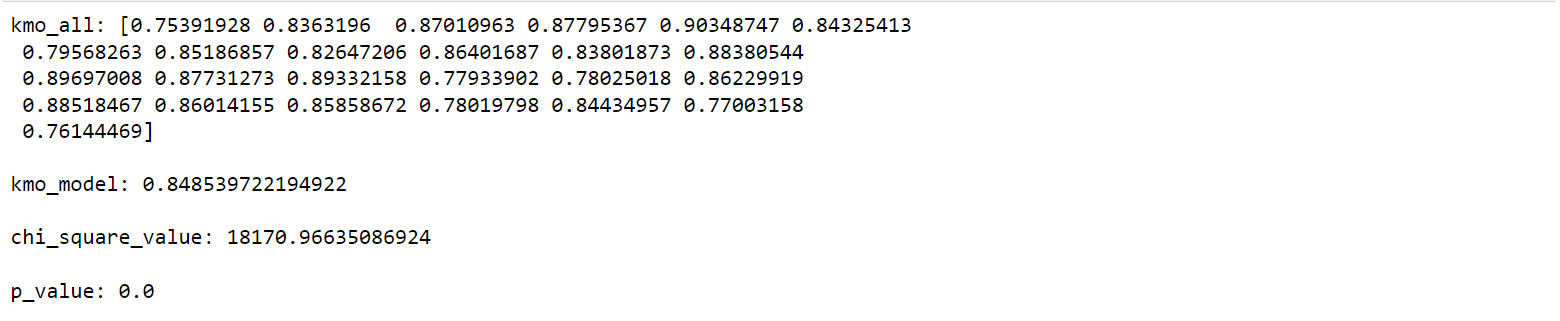
KMO检验表明KMO统计量值为0.85，表明数据适合进行因子分析；同时巴特莱特球形检验p值为0，拒绝原假设（相关系数矩阵为单位矩阵），变量之间存在相关关系，适合做因子分析。

6.3 提取公因子

进行探索性因子分析，确定提取公因子个数。计算相关系数矩阵特征根和特征向量

# 探索性因子分析
fa = FactorAnalyzer(25, rotation=None)
fa.fit(df)

# 相关系数矩阵的特征根和特征向量
ev, v = fa.get_eigenvalues()
ev, v

# 根据特征根>1发现，可提取6个公因子

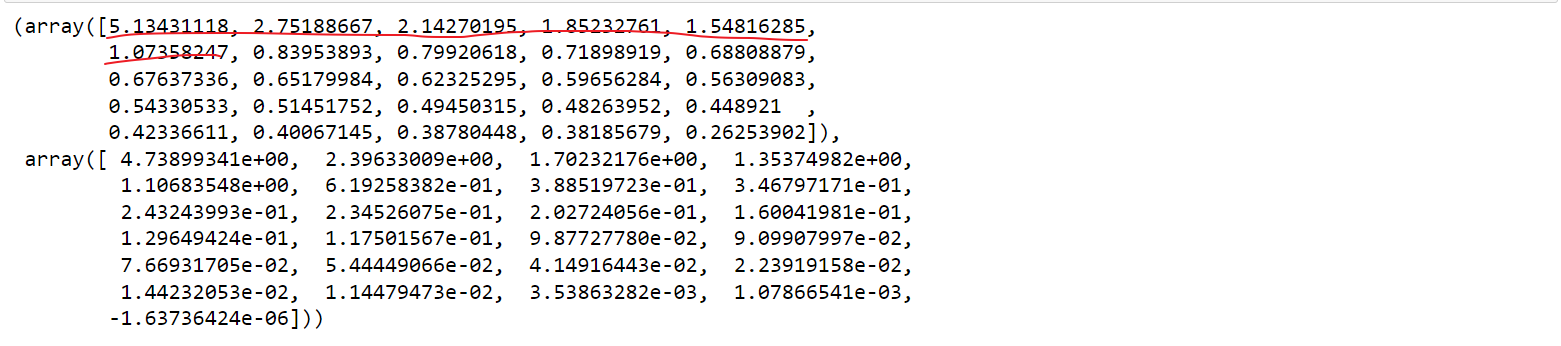
绘制碎石图进一步确定因子个数

# 绘制碎石图，选择因子数
plt.scatter(range(1,df.shape[1]+1),ev)
plt.plot(range(1,df.shape[1]+1),ev)
plt.title('Scree Plot')
plt.xlabel('Factors')
plt.ylabel('Eigenvalue')
plt.grid()
plt.show()

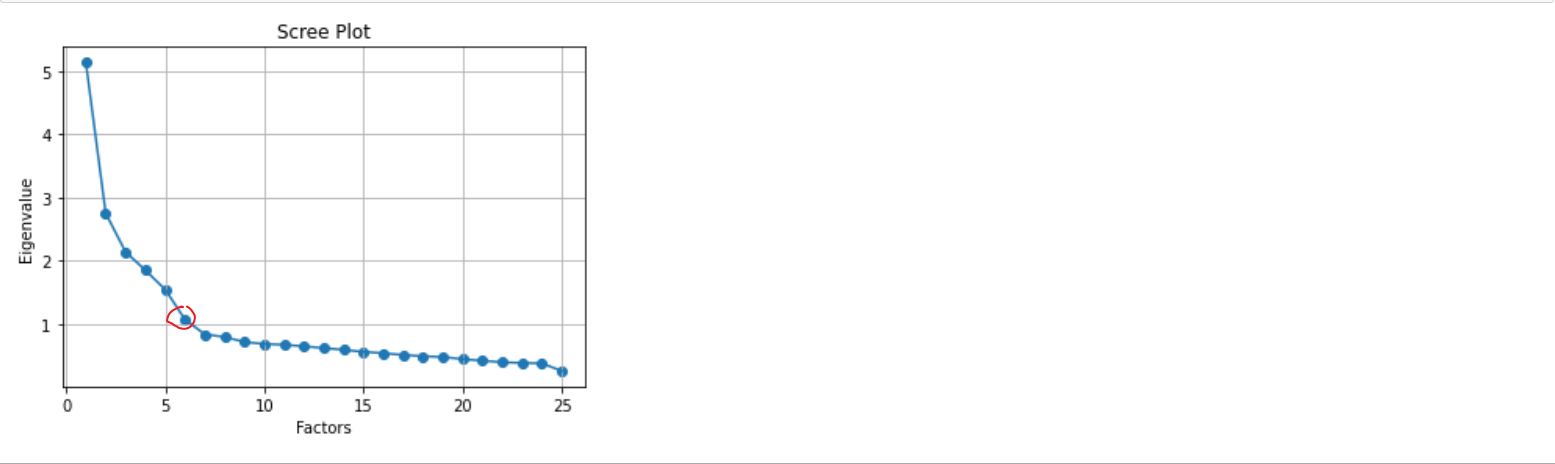
6.4 因子旋转

建立明确的因子分析模型，并对因子进行方差最大化的正交旋转。

# 建立因子分析模型

fa_six = FactorAnalyzer(6, rotation="varimax")
fa_six.fit(df)

# 输出因子的载荷

fa_six.loadings_

# pd.DataFrame(fa_six.loadings_, index=df.columns)

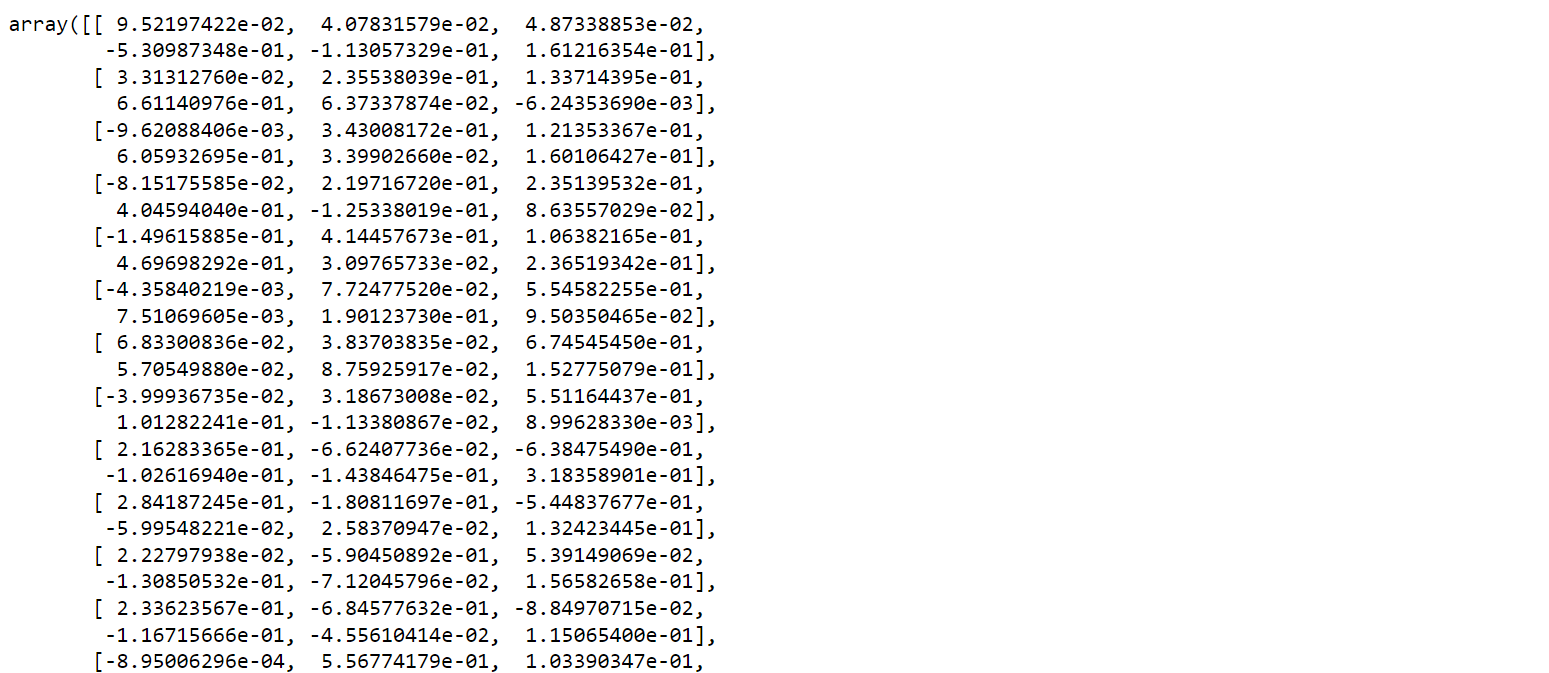
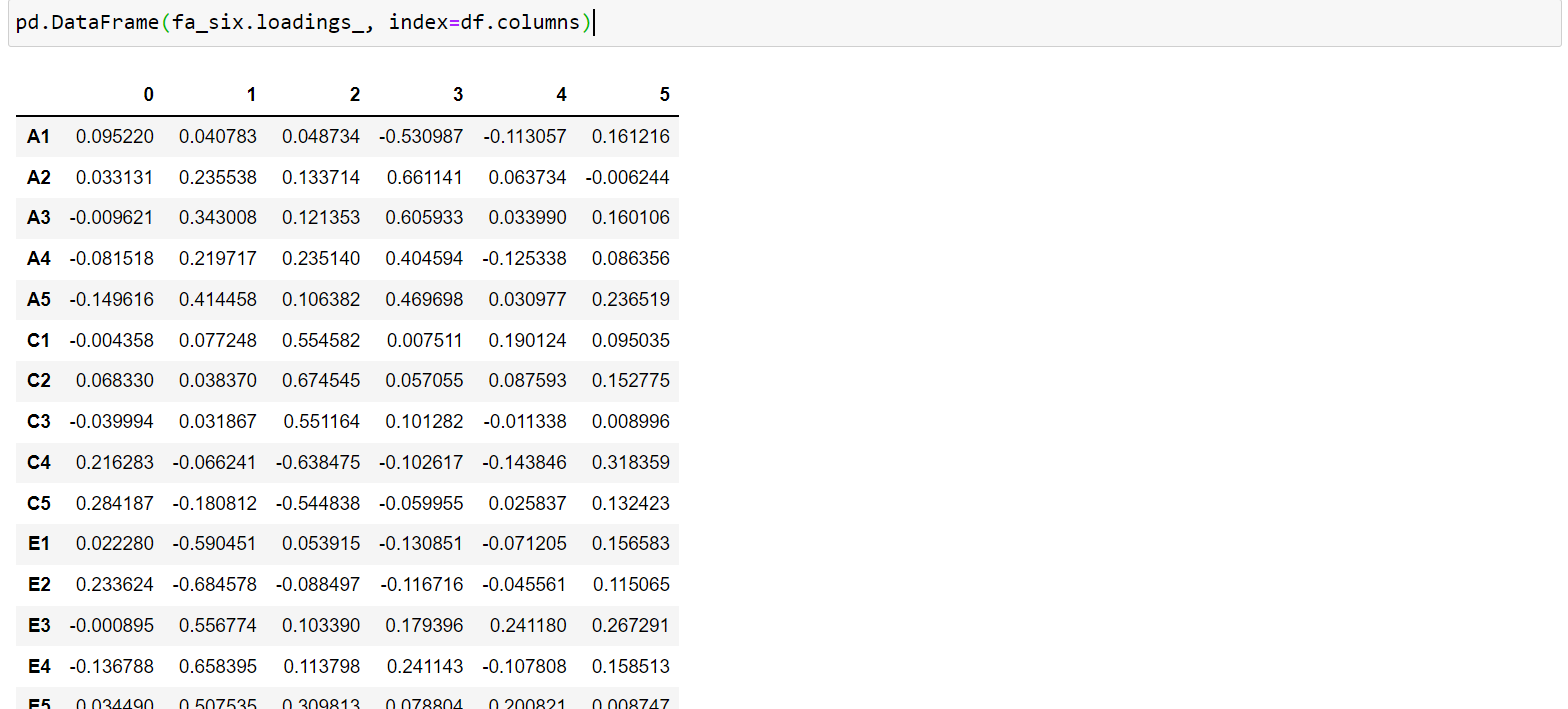
结果看起来并不直观，无法看出哪些因子对变量的解释程度较高，对数据进行可视化展示结果。

import seaborn as sns
df_cm = pd.DataFrame(np.abs(fa_six.loadings_), index=df.columns)

plt.figure(figsize = (14,14))
ax = sns.heatmap(df_cm, annot=True, cmap="BuPu")

# 设置y轴的字体的大小
ax.yaxis.set_tick_params(labelsize=15)

plt.title('Factor Analysis', fontsize='xx-large')
# 设置y轴标签
plt.ylabel('Personality items', fontsize='xx-large')

# 保存图片
# plt.savefig(r'C:\Users\Desktop\factorAnalysis.png', dpi=500)

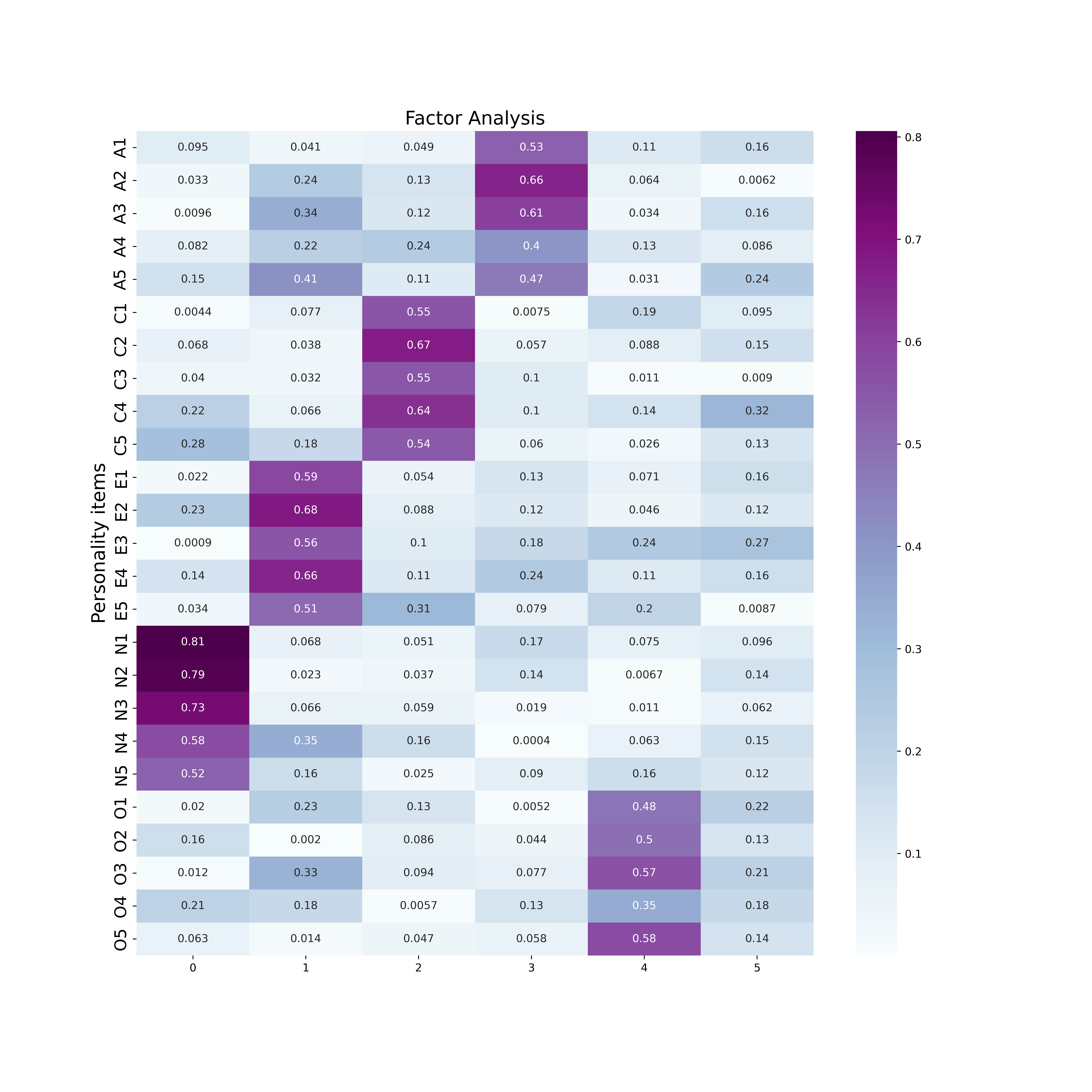
由上图，因子6对所有变量都没有高负荷，也不容易解释，需要调整因子个数，选择5个公因子。重复上面的步骤：

# 建立因子分析模型，设置公因子个数为5
fa_five = FactorAnalyzer(5, rotation="varimax")
fa_five.fit(df)

import seaborn as sns
df_cm = pd.DataFrame(np.abs(fa_five.loadings_), index=df.columns)

plt.figure(figsize = (14,14))
ax = sns.heatmap(df_cm, annot=True, cmap="BuPu")

# 设置y轴的字体的大小
ax.yaxis.set_tick_params(labelsize=15)

plt.title('Factor Analysis', fontsize='xx-large')
# 设置y轴标签
plt.ylabel('Personality items', fontsize='xx-large')

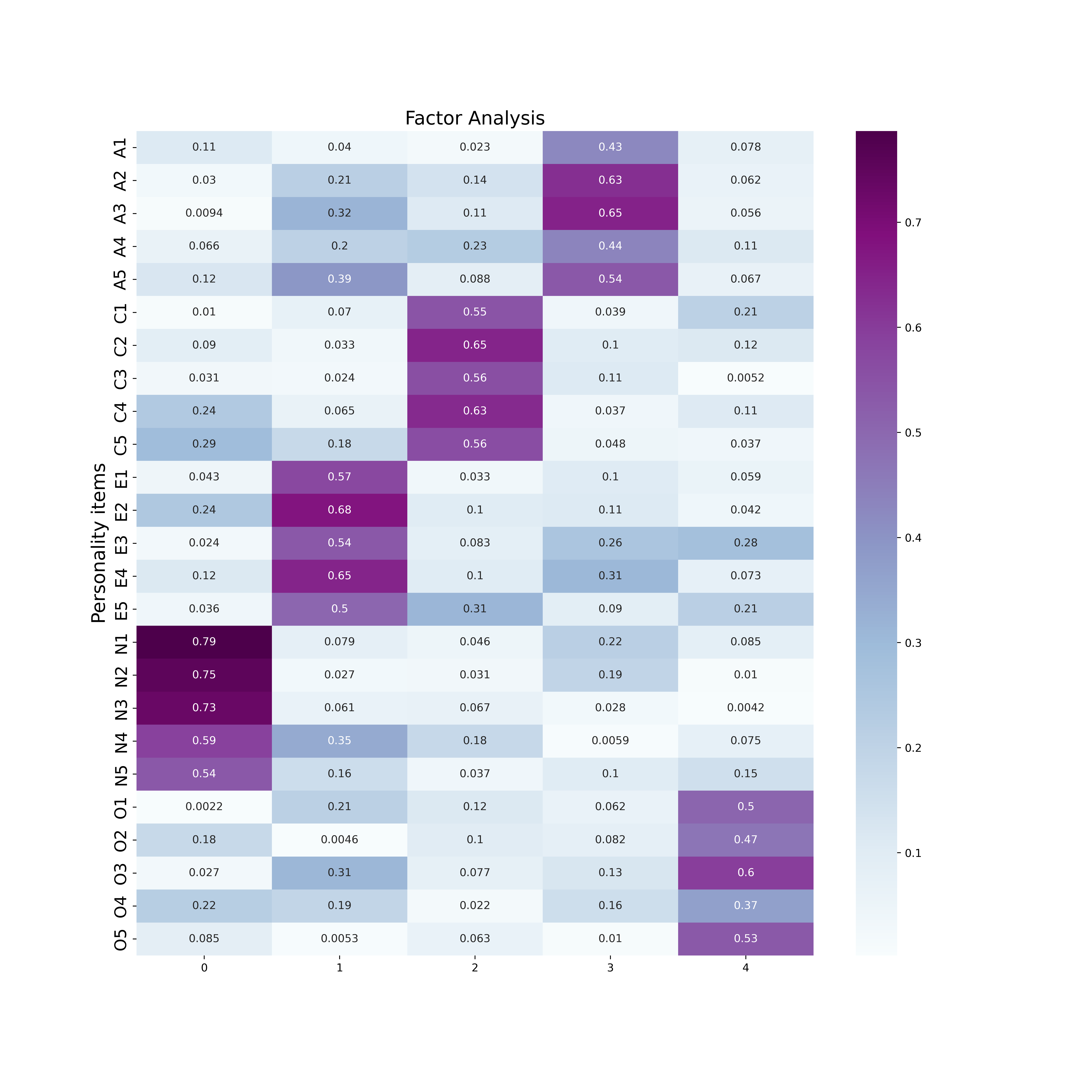
根据上图结果：

因子1在变量（N1, N2, N3, N4, N5）上具有较高载荷，可定义因子1为神经质因子。

因子2在变量（E1, E2, E3, E4, E5）上具有较高载荷，可定义因子2为外向型因子。

因子3在变量（C1, C2, C3, C4, C5）上具有较高载荷，可定义因子3为尽责性因子。

因子4在变量（A1, A2, A3, A4, A5）上具有较高载荷，可定义因子4为认同性因子。

因子5在变量（O1, O2, O3, O4, O5）上具有较高载荷，可定义因子5为开放性因子。

# 方差累计贡献
fa_v = fa_five.get_factor_variance()
fa_dt = pd.DataFrame({
    "特征根": fa_v[0],
    "方差贡献率": fa_v[1],
    "方差累计贡献率": fa_v[2]
})

fa_dt

5个因子的特征值之和占特征值总和的42.36%，也可以说5个因子解释了全部变量的42.36%的信息。

6.5 计算因子得分

# 计算因子得分
score = fa_five.transform(df)
score


# 计算综合得分
x = score @ (fa_v[1])
result = pd.DataFrame(x, columns=["综合得分"], index=df.index)
result.sort_values(by="综合得分", ascending=False, inplace=True)
result

完整代码：

import numpy as np
import pandas as pd

from factor_analyzer import FactorAnalyzer
from factor_analyzer.factor_analyzer import calculate_kmo
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity

import matplotlib.pyplot as plt
%matplotlib inline


# 导入数据
df = pd.read_csv(r'C:\Users\wy\Desktop\bfi.csv')
df.head()

# 删除无关列
df.drop(["gender", "education", "age", "Unnamed: 0"], axis=1, inplace=True)

# 查看是否有缺失值
df.isnull().sum()

# 删除缺失值
df.dropna(inplace=True)

# 因子分析可靠性检验
kmo_all, kmo_model = calculate_kmo(df)
chi_square_value, p_value = calculate_bartlett_sphericity(df)

print("kmo_all:", kmo_all, end="\n\n")
print("kmo_model:", kmo_model, end="\n\n")
print("chi_square_value:", chi_square_value, end="\n\n")
print("p_value:", p_value)

# 探索性因子分析
fa = FactorAnalyzer(25, rotation=None)
fa.fit(df)

# 相关系数矩阵的特征根和特征向量
ev, v = fa.get_eigenvalues()
ev, v

# 根据特征根>1发现，可提取6个公因子

# 绘制碎石图，选择因子数
plt.scatter(range(1,df.shape[1]+1),ev)
plt.plot(range(1,df.shape[1]+1),ev)
plt.title('Scree Plot')
plt.xlabel('Factors')
plt.ylabel('Eigenvalue')
plt.grid()
plt.show()


# 建立因子分析模型
fa_six = FactorAnalyzer(6, rotation="varimax")
fa_six.fit(df)

# 输出因子的载荷
fa_six.loadings_


# 建立因子分析模型

fa_five = FactorAnalyzer(5, rotation="varimax")  # 根据6个公因子的热力图发现Factor6在每个变量上均无载荷。故调整为5个公因子。
fa_five.fit(df)

import seaborn as sns
df_cm = pd.DataFrame(np.abs(fa_five.loadings_), index=df.columns)

plt.figure(figsize = (14,14))
ax = sns.heatmap(df_cm, annot=True, cmap="BuPu")

# 设置y轴的字体的大小
ax.yaxis.set_tick_params(labelsize=15)

plt.title('Factor Analysis', fontsize='xx-large')
# 设置y轴标签
plt.ylabel('Personality items', fontsize='xx-large')

# 方差累计贡献

fa_v = fa_five.get_factor_variance()
fa_dt = pd.DataFrame({
    "特征根": fa_v[0],
    "方差贡献率": fa_v[1],
    "方差累计贡献率": fa_v[2]
})

fa_dt

# 计算因子得分
score = fa_five.transform(df)
score

# 计算综合得分
x = score @ (fa_v[1])
result = pd.DataFrame(x, columns=["综合得分"], index=df.index)
result.sort_values(by="综合得分", ascending=False, inplace=True)
result

参考：

因子分析——python

Introduction to Factor Analysis in Python

因子分析——附数据下载

因子分析

posted @ 2022-04-17 14:22  没有风格的Wang  阅读(2155)  评论(0)  编辑  收藏  举报