图

1.1图的思维导图

 

 

1.2 图结构学习体会

1．深度优先遍历的递归定义

　　假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点)，则深度优先遍历可定义如下：首先访问出发点v，并将其标记为已访问过；然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止。

　　图的深度优先遍历类似于树的前序遍历。采用的搜索方法的特点是尽可能先对纵深方向进行搜索。这种搜索方法称为深度优先搜索(Depth-First Search)。相应地，用此方法遍历图就很自然地称之为图的深度优先遍历

2.基本实现思想：

（1）访问顶点v；

（2）从v的未被访问的邻接点中选取一个顶点w，从w出发进行深度优先遍历；

（3）重复上述两步，直至图中所有和v有路径相通的顶点都被访问到。

3.伪代码

递归实现

（1）访问顶点v；visited[v]=1；//算法执行前visited[n]=0

（2）w=顶点v的第一个邻接点；

（3）while（w存在）  

           if（w未被访问）

                   从顶点w出发递归执行该算法； 
           w=顶点v的下一个邻接点；

非递归实现

 （1）栈S初始化；visited[n]=0；

 （2）访问顶点v；visited[v]=1；顶点v入栈S

 （3）while(栈S非空)

            x=栈S的顶元素(不出栈)；

            if(存在并找到未被访问的x的邻接点w)

                    访问w；visited[w]=1；

                    w进栈;

            else

                     x出栈；

广度优先遍历

 1.广度优先遍历定义

 图的广度优先遍历BFS算法是一个分层搜索的过程，和树的层序遍历算法类同，它也需要一个队列以保持遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。 

2.基本实现思想

（1）顶点v入队列。

（2）当队列非空时则继续执行，否则算法结束。

（3）出队列取得队头顶点v；访问顶点v并标记顶点v已被访问。

（4）查找顶点v的第一个邻接顶点col。

（5）若v的邻接顶点col未被访问过的，则col入队列。

（6）继续查找顶点v的另一个新的邻接顶点col，转到步骤（5）。

        直到顶点v的所有未被访问过的邻接点处理完。转到步骤（2）。

广度优先遍历图是以顶点v为起始点，由近至远，依次访问和v有路径相通而且路径长度为1，2，……的顶点。为了使“先被访问顶点的邻接点”先于“后被访问顶点的邻接点”被访问，需设置队列存储访问的顶点。

3.伪代码

（1）初始化队列Q；visited[n]=0；

（2）访问顶点v；visited[v]=1；顶点v入队列Q；

（3） while（队列Q非空）   

              v=队列Q的对头元素出队；

              w=顶点v的第一个邻接点；

             while（w存在） 

                     如果w未访问，则访问顶点w；

                     visited[w]=1；

                     顶点w入队列Q；

                     w=顶点v的下一个邻接点。

Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列，接着按照顺序选取每条边，如果这条边的两个端点不属于同一集合，那么就将它们合并，直到所有的点都属于同一个集合为止。至于怎么合并到一个集合，那么这里我们就可以用到一个工具——-并查集(不知道的同学请移步：Here)。换而言之，Kruskal算法就是基于并查集的贪心算法。

Prim算法它是从点的方面考虑构建一颗MST，大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。

Dijkstra算法采用的是一种贪心的策略，声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合：T，初始时，原点 s 的路径权重被赋为 0 （dis[s] = 0）。若对于顶点 s 存在能直接到达的边（s,m），则把dis[m]设为w（s, m）,同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。初始时，集合T只有顶点s。 
然后，从dis数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入到T中，OK，此时完成一个顶点， 
然后，我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dis中的值。 
然后，又从dis中找出最小值，重复上述动作，直到T中包含了图的所有顶点。

拓扑排序 在有向图中选一个没有前驱的顶点并且输出

从图中删除该顶点和所有以它为尾的弧（白话就是：删除所有和它有关的边）

重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点为止，后者代表我们的有向图是有环的，因此，也可以通过拓扑排序来判断一个图是否有环。

  1. PTA实验作业

7-2 排座位

2.2 设计思路（伪代码或流程图)

 

 

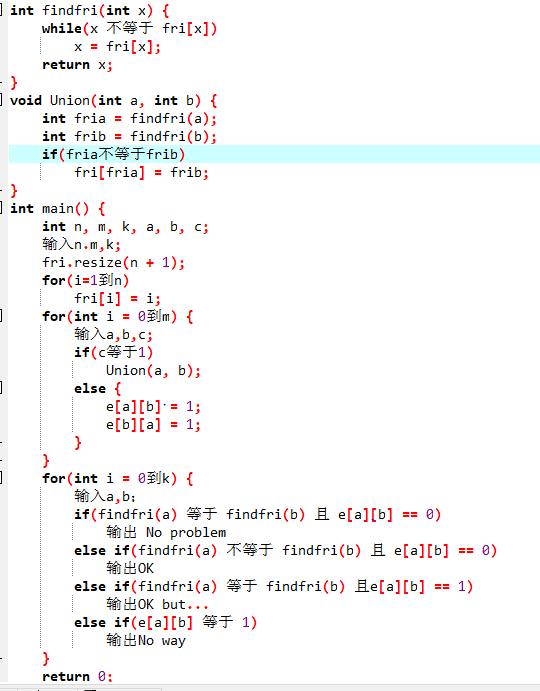
2.3 代码截图

 

 

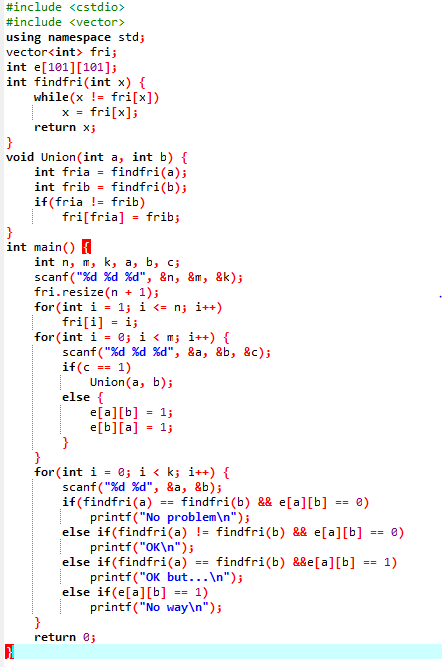
 2.4 PTA提交列表说明

 

 

 

7-7 旅游规划

2.2 设计思路（伪代码或流程图)

 

 

 

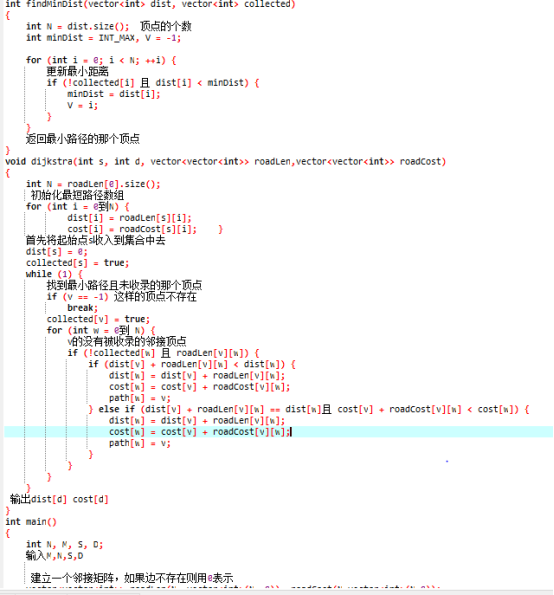
2.3 代码截图

 

 

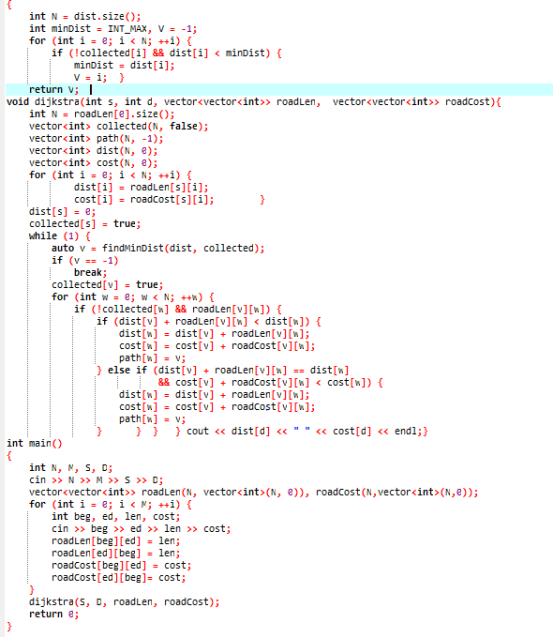
2.4 PTA提交列表说明

 

 

7-4 公路村村通

2.2 设计思路（伪代码或流程图)

 

 

2.3 代码截图

 

 

2.4 PTA提交列表说明

 

 

3.截图本周题目集的PTA最后排名

 

4. 阅读代码（必做，1分）

[cpp] view plain copy
 
  1. #include<stdio.h>  
  2. #include<stdlib.h>  
  3. /* 
  4. 图的表示方法 
  5. DG（有向图）或者DN（有向网）：邻接矩阵、邻接表（逆邻接表--为求入度）、十字链表 
  6. UDG（无向图）或者UDN（无向网）：邻接矩阵、邻接表、邻接多重表 
  7. */  
  8. #define MAX_VERTEX_NUM 10//最大顶点数目  
  9. #define NULL 0  
  10. //typedef int VRType;//对于带权图或网，则为相应权值  
  11. typedef int VertexType;//顶点类型  
  12. //typedef enum GraphKind {DG, DN, UDG, UDN};  //有向图：0，有向网：1，无向图：2，无向  
  13.   
  14. typedef struct ArcNode{   
  15.     int tailvex, headvex;//该弧的弧尾（起点）和弧头（终点）所指向的顶点的在图中位置  
  16.     struct ArcNode *tailNextarc, *headNextArc;//分别为指向弧尾（起点）相同的弧的下一条弧的指针、弧头（终点）相同的弧的下一条弧的指针  
  17. }ArcNode;//弧结点信息  
  18.   
  19. typedef struct VNode{  
  20.     VertexType data;//顶点信息  
  21.     ArcNode *firstIn;//指向第一条以该顶点为弧尾（起点）的指针  
  22.     ArcNode *firstOut;//指向第一条以该顶点的弧头（终点）的指针  
  23. }VNode, VexList[MAX_VERTEX_NUM];//顶点结点信息  
  24.   
  25. typedef struct{  
  26.     VexList vexs;//顶点向量  
  27.     int vexnum, arcnum;//图的当前顶点数和弧数  
  28.     //GraphKind kind;//图的种类标志  
  29. }OLGraph;//邻接表表示的图  
[cpp] view plain copy
 
  1. //若图G中存在顶点v，则返回v在图中的位置信息，否则返回其他信息  
  2. int locateVex(OLGraph G, VertexType v){  
  3.     for(int i = 0; i < G.vexnum; i++){  
  4.         if(G.vexs[i].data == v)  
  5.             return i;  
  6.     }  
  7.     return -1;//图中没有该顶点  
  8. }  
[cpp] view plain copy
 
  1. //采用十字链表表示法构造有向图G  
  2. void createDG(OLGraph &G){  
  3.     printf("输入顶点数和弧数如:(5,3):");  
  4.     scanf("%d,%d", &G.vexnum, &G.arcnum);  
  5.   
  6.     //构造顶点向量,并初始化  
  7.     printf("输入%d个顶点（以空格隔开如：v1 v2 v3）:", G.vexnum);  
  8.     getchar();//吃掉换行符  
  9.     for(int m = 0; m < G.vexnum; m++){  
  10.         scanf("v%d", &G.vexs[m].data);  
  11.         G.vexs[m].firstIn = NULL;//初始化为空指针////////////////重要！！！  
  12.         G.vexs[m].firstOut = NULL;  
  13.         getchar();//吃掉空格符  
  14.     }  
  15.   
  16.     //构造十字链表  
  17.     VertexType v1, v2;//分别是一条弧的弧尾和弧头（起点和终点）  
  18.     printf("\n每行输入一条弧依附的顶点（先弧尾后弧头）（如：v1v2）:\n");  
  19.     fflush(stdin);//清除残余后，后面再读入时不会出错  
  20.     int i = 0, j = 0;  
  21.     for(int k = 0; k < G.arcnum; k++){  
  22.         scanf("v%dv%d",&v1, &v2);  
  23.         fflush(stdin);//清除残余后，后面再读入时不会出错  
  24.         i = locateVex(G, v1);//弧起点  
  25.         j = locateVex(G, v2);//弧终点  
  26.           
  27.         //采用“头插法”在各个顶点的弧链头部插入弧结点  
  28.         ArcNode *p = (ArcNode *)malloc(sizeof(ArcNode));//构造一个弧结点，作为弧vivj的弧头（终点）  
  29.         p->tailvex = i;  
  30.         p->tailNextarc = G.vexs[i].firstOut;  
  31.         G.vexs[i].firstOut = p;  
  32.         p->headvex = j;  
  33.         p->headNextArc = G.vexs[j].firstIn;  
  34.         G.vexs[j].firstIn = p;  
  35.     }  
  36. }  
  1. //打印十字链表  
  2. void printOrthogonalList(OLGraph G){  
  3.     printf("\n");  
  4.     for(int i = 0; i < G.vexnum; i++){  
  5.         printf("以顶点v%d为弧尾的弧有为：", G.vexs[i].data);  
  6.         ArcNode *p = G.vexs[i].firstOut;  
  7.         while(p){  
  8.             printf("v%dv%d ", G.vexs[i].data, G.vexs[p->headvex].data);  
  9.             p = p->tailNextarc;  
  10.         }  
  11.         printf("\n");  
  12.     }  
  13.     printf("\n");  
  14. } 

 

posted on 2018-06-18 14:10  啊哈yy  阅读(134)  评论(0)  编辑  收藏  举报