查找
一、学习总结
1.1查找的思维导图

1.2 查找学习体会
在学习完查找后,了解了线性表的查找,树表的查找,哈希表的查找,其中哈希表的查找较为难以理解,还需多加深入学习。
2.PTA实验作业
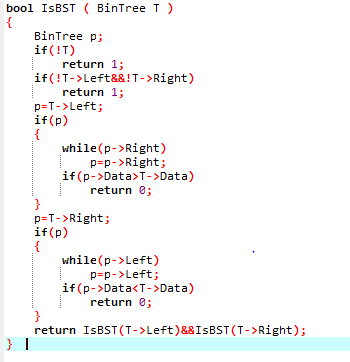
2.1 题目1:6-2 是否二叉搜索树
2.2 设计思路(伪代码或流程图)

2.3 代码截图
2.4 PTA提交列表说明

2.1 题目2:6-3 二叉搜索树中的最近公共祖先
2.2 设计思路(伪代码或流程图)
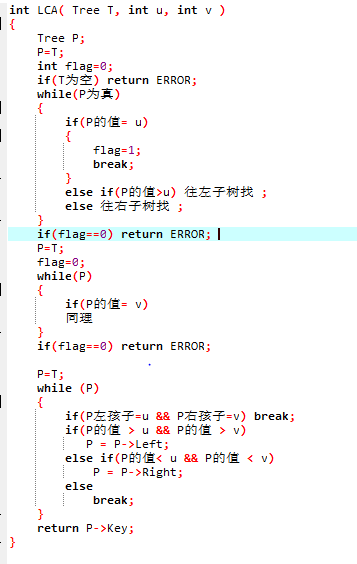
2.3 代码截图
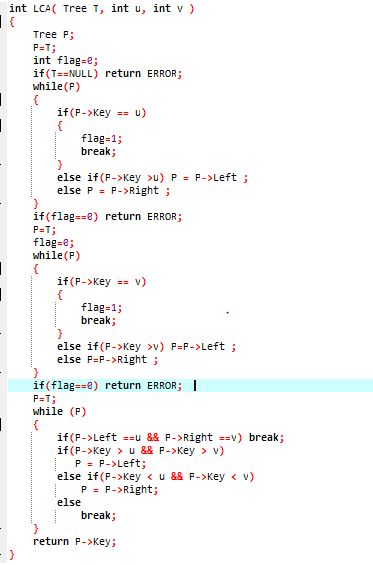
2.4 PTA提交列表说明


刚开始条件没有考虑周全没考虑到两节点之一是答案,两节点是兄弟等条件。
2.1 题目3:7-1 QQ帐户的申请与登陆
2.2 设计思路(伪代码或流程图)
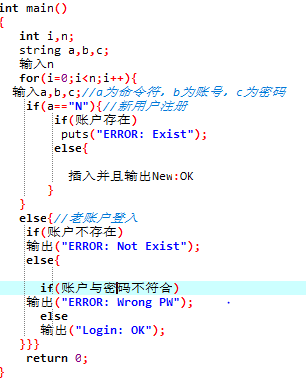
2.3 代码截图
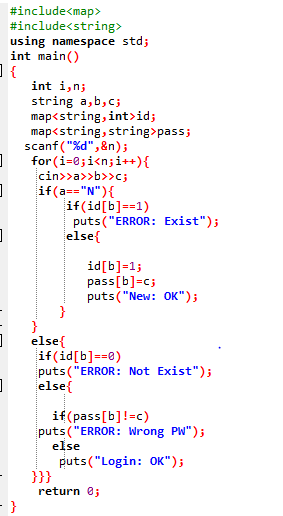
2.4 PTA提交列表说明

这题用到了map的用法,由于对于map用法不是很了解并且不能掌握如何应用,就参考了其他同学的做法。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

4. 阅读代码
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,及n=F(k)-1;
开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种
1)相等,mid位置的元素即为所求
2)>,low=mid+1,k-=2;
说明:low=mid+1说明待查找的元素在[mid+1,high]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找。
3)<,high=mid-1,k-=1。
说明:low=mid+1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个,所以可以递归 的应用斐波那契查找。
C++实现源码:
// 斐波那契查找.cpp
#include "stdafx.h"
#include <memory>
#include <iostream>
using namespace std;
const int max_size=20;//斐波那契数组的长度
/*构造一个斐波那契数组*/
void Fibonacci(int * F)
{
F[0]=0;
F[1]=1;
for(int i=2;i<max_size;++i)
F[i]=F[i-1]+F[i-2];
}
/*定义斐波那契查找法*/
int FibonacciSearch(int *a, int n, int key) //a为要查找的数组,n为要查找的数组长度,key为要查找的关键字
{
int low=0;
int high=n-1;
int F[max_size];
Fibonacci(F);//构造一个斐波那契数组F
int k=0;
while(n>F[k]-1)//计算n位于斐波那契数列的位置
++k;
int * temp;//将数组a扩展到F[k]-1的长度
temp=new int [F[k]-1];
memcpy(temp,a,n*sizeof(int));
for(int i=n;i<F[k]-1;++i)
temp[i]=a[n-1];
while(low<=high)
{
int mid=low+F[k-1]-1;
if(key<temp[mid])
{
high=mid-1;
k-=1;
}
else if(key>temp[mid])
{
low=mid+1;
k-=2;
}
else
{
if(mid<n)
return mid; //若相等则说明mid即为查找到的位置
else
return n-1; //若mid>=n则说明是扩展的数值,返回n-1
}
}
delete [] temp;
return -1;
}
int main()
{
int a[] = {0,16,24,35,47,59,62,73,88,99};
int key=100;
int index=FibonacciSearch(a,sizeof(a)/sizeof(int),key);
cout<<key<<" is located at:"<<index;
return 0;
}


