【学习笔记】带权二分
直线与凸壳的相切关系
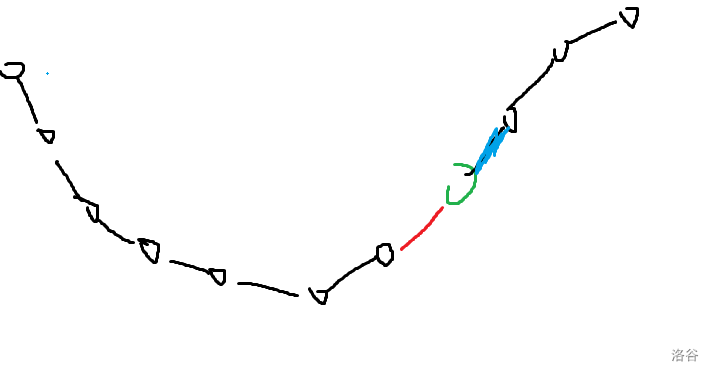
如果凸壳的斜率互不相同,凸壳上存在两点间的斜率是 \(k\) ,那么斜率为 \(k\) 的直线和凸壳有两个切点(如果存在相同的斜率那么可能切更多的点),如果不存在,则只有一个切点。
令红线的斜率为 \(k_1\) , 蓝线的斜率为 \(k_2\) 有且仅有 \(k\in [k_1,k_2]\) 的斜率能够切到绿点。
带权二分的基本原理与应用范围
带权二分一般解决的是形如这样的问题:
给定 \(n\) 个物品,要求从中恰好选出 \(m\) 个,满足某种限制,要求最大化收益 / 最小化价值,且如果不限定数目问题比较简单。
令 \(g(i)\) 为选出恰好 \(i\) 个物品的最大化收益 ,满足于函数 \((i,g(i))\) 是凸壳。
下面以上凸包(从左到右斜率递减)为例子。
我们的目标是求出 \(g(m)\) 。
做法是,二分一个斜率\(k\),然后找到斜率为 \(k\) 的切这个凸壳的直线切于哪一点。
可以发现,随着 \(k\) 的减小,这条直线切的点会越来越靠右,就像这样:
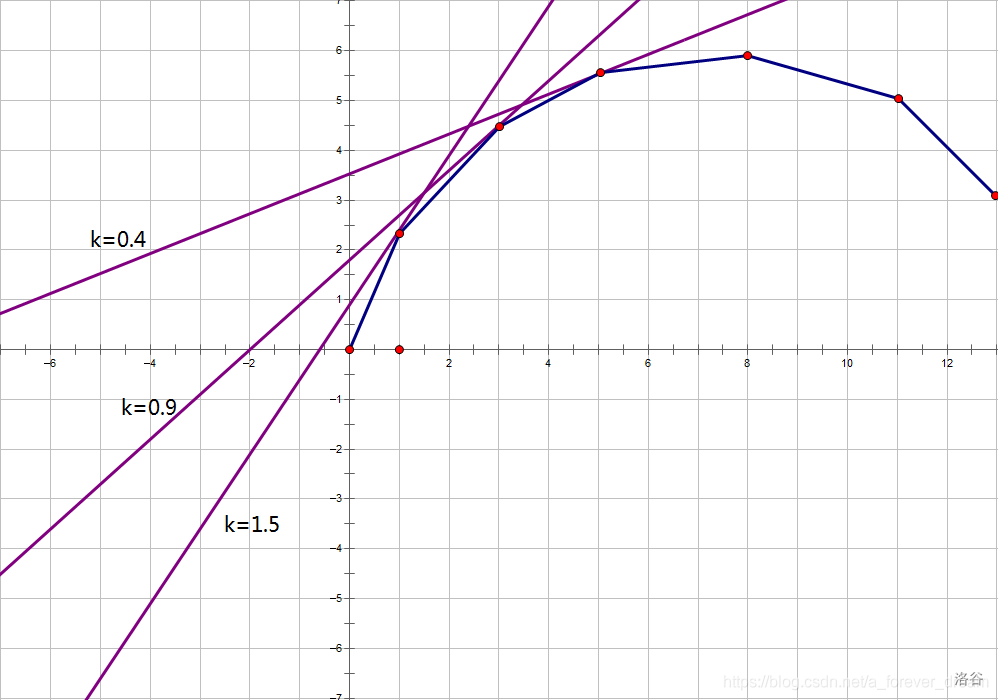
于是我们二分 \(k\) 直到这条直线与凸壳的切点为 \((m,g(m))\) 。
问题变成了:当二分出一个 \(k\) 时,怎么求被切的点是谁。
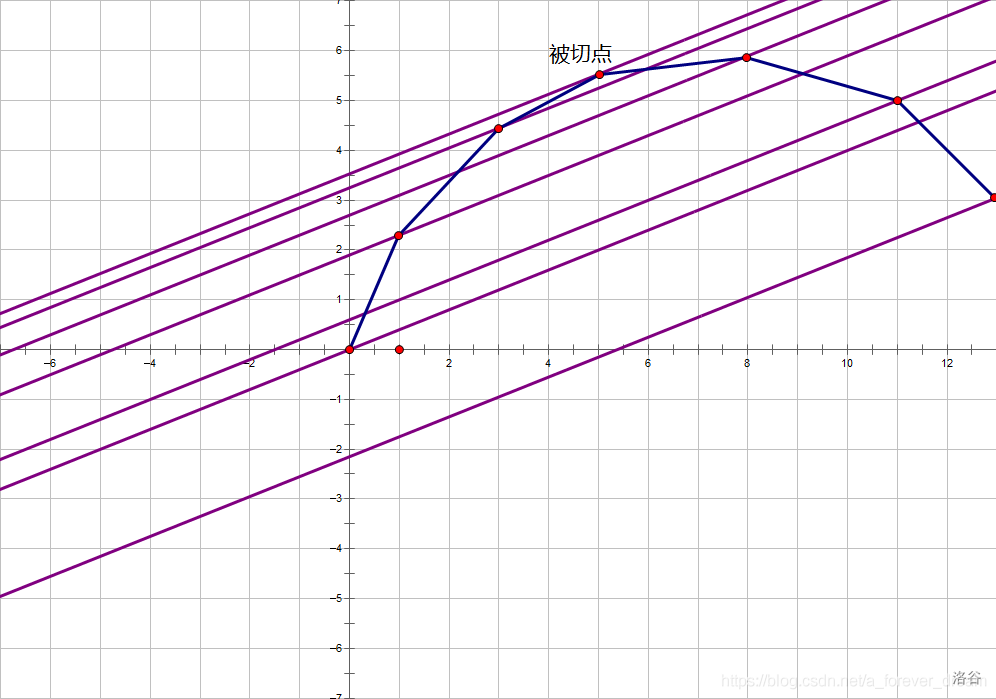
可以发现,所有斜率为 \(k\) 且与凸壳有交点的直线中,截距最大的那一条直线,就是与凸壳相切的直线。
设直线 \(y=kx+b\) 与凸壳 \(g(x)\) 交于点 \((i,g(i))\) ,那么有方程 \(ki+b=g(i)\) ,移项:
考虑 \(g(i)-ki\) 的组合意义:\(g(i)\) 表示选恰好 \(i\) 个的最大化收益,那么 \(g(i)-ki\) 等价于每个物品价值 \(-k\) 后选恰好 \(i\) 个的最大化收益。
那么 \(b\) 就等价于所有物品价值 \(-k\) 后,没有数量限制的最大化收益。最优解取到的个数 \(i\) 即与凸壳交点的横坐标。
带权二分的细节与边界
如何确定实数二分与整数二分
若函数的定义域以及凸壳斜率(凸壳相邻两点连线的斜率,即凸壳上相邻两点的差分除以间距)都取在整数上一般来说整数二分就好。
因为一定存在一个整数斜率k满足切点之一是 $m $(存在一个 \(m\) 与相邻点之间的斜率与 \(k\) 相同)。
如何确定二分边界
令 \(\Delta\) 为凸壳相邻两点函数值的能取到的最大差分,那么二分边界为 \([-\Delta,+\Delta]\) 。
例题
P2619 [国家集训队]Tree I
题目描述
给你一个无向带权连通图,每条边是黑色或白色。
让你求一棵最小权的恰好有 \(need\) 条白色边的生成树。 题目保证有解。
数据范围
\(V\le 5\times 10^4,E\le 10^5\) ,边权均为 \([1,100]\) 中的整数。
题解
分黑白考虑。
如果两点之间没有黑边,我们假设连了一条权值为$ +\infty$ 的黑边。
找出黑边形成的最小生成树。
每次加入一条最小的白边,删除一条可以删的最大的黑边,所以也具有凸性质。
排序要优先把白边排到前面,这样我们最后求得的是切到的最靠右 \(x\) 最大的点。
P5633 最小度限制生成树
题目描述
给你一个有 \(n\) 个节点,\(m\) 条边的带权无向图,你需要求得一个生成树,使边权总和最小,且满足编号为 \(s\) 的节点正好连了 \(k\) 条边。
不保证有解。
数据范围
\(1\le n\le 5\times 10^4,1\le m\le 5\times 10^5,1\le k\le 100,0\le w\le 3\times 10^4\) 。
题解
发现题意与上题本质相同,我们将所有与点 \(s\) 相连的边染成白色,其他边染成黑色。
问题等价于求一棵最小权的恰好有 \(k\) 条边的生成树。
注意到,本题 不保证有解 。
在上一题的题解没有着重讨论整数二分的实现细节与正确性。
首先我们需要证明:凸壳的定义域 为 \([l,r]\cap Z\) 即定义域是连续的一段整数区间。
对于这一性质的证明并不困难,任意一棵包含 \(i\) 条白边的生成树都可以看成包含 \(i-1\) 条白边的生成树使用一条非树边(白边)替换一条生成树中的黑边。因此,凸壳的定义域一定是连续的一段整数区间。
那么凸壳上的斜率,均为正整数,因此可以直接在整数上二分。
对于判是否有解相当于判 \(k\) 是否在凸壳的定义域内。
而对于整数二分,每次 \(\text{check}\) 的时,排序要优先把白边排到前面,这样我们最后求得的是切到的最靠右 \(x\) 最大的点。
那么我们最后二分出来的斜率,就是 **切到的最靠右的点大于等于 \(k\) ** 的最小的斜率。
因为切到固定的点的斜率是上下界是能够确定的,所以对于凸壳定义域内的点 \(p\in (l,r]\) ,二分出来的斜率一定是 \(g(p)-g(p-1)\) ,如果 \(k\) 在值域内二分出来的值域一定也是 \(g(k)-g(k-1)\) ,这个斜率能够切到的最右点就是我们 \(\text{kruskal}\) 函数返回的答案。
std::pair<int,int> kruskal(int k) {
std::vector<edges> e; int l0 = 0,l1 = 0;
for (int i = 0; i < m; i++) {
if (l1 >= edge[1].size()) {
e.push_back(edge[0][l0]); e[i].val -= k; ++l0; continue;
}
if (l0 >= edge[0].size() || edge[1][l1].val < edge[0][l0].val - k) {
e.push_back(edge[1][l1]); ++l1;
} else {
e.push_back(edge[0][l0]); e[i].val -= k; ++l0;
}
} int cnt = 0,ans = 0; rep(i,1,n) fa[i] = i;
for (int i = 0; i < e.size(); i++) {
if (get(e[i].u) == get(e[i].v)) continue;
merge(e[i].u,e[i].v); ans += e[i].val;
if(e[i].col == 0) ++cnt;
}
return {cnt,ans};
}
如果二分出来的斜率能够切到的最右点恰好等于 \(k\) ,那么 \(k\) 一定在凸壳的定义域内。
如果二分出来的斜率能够切到的最右点在 \(k\) 左边,显然 \(k\) 一定不在凸壳的定义域内。
如果二分出来的斜率能够切到的最右点在 \(k\) 右边,那么我们需要判断这条直线能不能切到 \(k\) 点。
这里我们采用组合意义判定:
- 斜率 \(p\) 能够切到点 \(k\) 当且仅当存在一棵包括 \(k\) 条边的生成树,满足边权和恰好为
kruskal(p).second。
bool check(int k,int val) {
std::vector<edges> e; int l0 = 0,l1 = 0;
for (int i = 0; i < m; i++) {
if (l1 >= edge[1].size()) {
e.push_back(edge[0][l0]); e[i].val -= k; ++l0; continue;
}
if (l0 >= edge[0].size() || edge[1][l1].val < edge[0][l0].val - k) {
e.push_back(edge[1][l1]); ++l1;
} else {
e.push_back(edge[0][l0]); e[i].val -= k; ++l0;
}
} int cnt = 0,ans = 0; rep(i,1,n) fa[i] = i;
for (int i = 0; i < e.size(); i++) {
if (get(e[i].u) == get(e[i].v)) continue;
if (cnt == need && e[i].col == 0) continue;
merge(e[i].u,e[i].v); ans += e[i].val;
if(e[i].col == 0) ++cnt;
}
int cc = 0;
rep(i,1,n) if (fa[i] == i) ++ cc;
if (cc > 1) return false;
if (ans != val) return false;
return true;
}
P4767 [IOI2000]邮局
题目描述
高速公路旁边有一些村庄。高速公路表示为整数轴,每个村庄的位置用单个整数坐标标识。没有两个在同样地方的村庄。两个位置之间的距离是其整数坐标差的绝对值。
邮局将建在一些,但不一定是所有的村庄中。为了建立邮局,应选择他们建造的位置,使每个村庄与其最近的邮局之间的距离总和最小。
你要编写一个程序,已知村庄的位置和邮局的数量,计算每个村庄和最近的邮局之间所有距离的最小可能的总和。
数据范围
\(1\le P\le 300,P\le V\le 3000\)
题解 (四边形不等式证明待填!)
首先,将所有村庄的坐标排序。
我们考虑固定每个邮局的位置为 \(pos[1],pos[2]...pos[P]\) 。
可以发现,每个邮局 “分管” 一段连续的区间,该段区间内的村庄对答案的贡献均为村庄与该邮局的距离。
对于这个问题有两种 DP 方式:
- 一种是考虑枚举最后一个邮局的位置。令 \(f[i][j][0/1]\) 为考虑前 \(i\) 个村庄,建 \(j\) 个邮局且第 \(i\) 个村庄 不建 / 建 邮局的最小花费。
- 一种是考虑枚举每个邮局 “分管” 的区间(间接枚举邮局的放置位置),令 \(f[i][j]\) 为考虑前 \(i\) 个村庄,建 \(j\) 个邮局的最小花费。 \(w(l,r)\) 为在 \([l,r]\) 的村庄建一个邮局,区间 \([l,r]\) 内部村庄的最小花费。转移枚举最后一段 “分管” 区间即可。
其中后者转移的复杂度是不受值域的限制的且转移较为简单。
经过 打表 发现,\(i\in [1,n]\cap Z,(i,f[n][i])\) 构成的点集是下凸壳。
而如果没有钦定数量的限制,第二种 DP 可以优化到 \(O(n^2)\) 的复杂度。
因为 \(m\) 一定在凸壳的定义域上,且凸壳中的斜率均为整数,直接在整数上带权二分即可。
对于凸壳的证明似乎要四边形不等式。待填!
P4383 [八省联考2018]林克卡特树
题目描述
小 L 最近沉迷于塞尔达传说:荒野之息(The Legend of Zelda: Breath of The Wild)无法自拔,他尤其喜欢游戏中的迷你挑战。
游戏中有一个叫做 LCT 的挑战,它的规则是这样子的:现在有一个 \(N\) 个点的树,每条边有一个整数边权 \(v_i\),若 \(v_i \geq 0\),表示走这条边会获得 \(v_i\) 的收益;若 \(v_i \lt 0\) ,则表示走这条边需要支付 \(-v_i\) 的过路费。小 L 需要控制主角 Link 切掉(Cut)树上的恰好 \(K\) 条边,然后再连接 \(K\) 条边权为 0 的边,得到一棵新的树。接着,他会选择树上的两个点 \(p,q\),并沿着树上连接这两点的简单路径从 \(p\) 走到 \(q\),并为经过的每条边支付过路费/ 获取相应收益。
海拉鲁大陆之神 TemporaryDO 想考验一下 Link。他告诉 Link,如果 Link 能切掉合适的边、选择合适的路径从而使 总收益 - 总过路费 最大化的话,就把传说中的大师之剑送给他。
小 L 想得到大师之剑,于是他找到了你来帮忙,请你告诉他,Link 能得到的 总收益 - 总过路费 最大是多少。
数据范围
\(1\le N\le 3\times 10^5,0\le K\le 3\times 10^5,K < N,1\le x_i,y_i\le N,|v_i|\le 10^6\) 。
题解
考虑 \(k=1\) 的情况:问题等价于切断一条边,将树分为两个联通块,在两个连通块内分别求直径,将直径的端点加边相邻。
并且我们发现可以扩展到 \(k > 1\) 的情况:问题等价于切断 \(k\) 条边,将树分为 \(k+1\) 个联通块,在 \(k+1\) 个连通块内分别求直径,将直径的端点加边相邻。
那么直观来说,问题等价于选定 \(k+1\) 条不相交的路径,使得路径权值和最大。
并且对于任意一种选定 \(k+1\) 条不相交的路径的方案,我们都可以断恰好 \(k\) 条边使得任意两条路径不在同一个连通块内 (考虑两条在同一连通块的两条路径的 LCA 的 LCA,每次断边两边的连通块一定包含路径且每次让关于路径的连通块个数 + 1) 。
一个直接的 \(\text{DP}\) 是令 \(f[u][j][0/1/2]\) 表示以 \(u\) 为根的子树中选恰好 \(j\) 条不相交的链,且 \(u\) 的度数为 \(0/1/2\) 的方案数 (不在路径上 / 在链顶 / 为链的 LCA )。
感性理解 + 打表发现其是一个上凸壳,将第二维去掉之后带权二分即可。



